小波变换在公路技术状况评定中的应用

王旺，侯信

(1.广东交科检测有限公司，广东 广州 510420；2.长沙华南土木工程监理有限公司)

随着中国高速公路建设的快速发展，路面使用性能状况如何，应采取什么样的养护决策，都是日常养护工作中公路工作者尤其是管理方关心的问题，也是日常养护工作的重点。而判断路面使用性能状况的前提就是对路面状况进行检测、调查，并按文献[1]中的相关规定进行评定，进而采取相应养护措施。已有研究表明：路面弯沉检测数据并不服从正态分布，因此评定标准中关于路面结构强度(PSSI)的计算并不准确；且随着检测设备的自动化程度越来越高，检测数据受环境误差、仪器误差及系统误差等的影响越来越大。因此，如检测数据不经处理就进行计算、评定路面技术状况，必然不能反映路面状况的真实情况，影响路面养护决策的制定。一些研究者采用小波变换对公路技术状况评定的部分指标进行了处理，并使其更加真实地反映了所代表的路面真实状况。毛庆洲提出了一种基于小波变换的路面平整度测量数据精确处理的新算法，解决检测车变速运动环境下检测精度低且稳定性差的难题。但这些研究皆没有系统地进行公路技术状况评定。该文拟采用小波变换进行公路技术状况评定，并提出新的评价方法，为公路技术状况评定及路面养护工作提供有价值的参考。

1 小波变换及消噪原理

1.1 小波变换

小波变换是在傅立叶变换的基础上发展而来的一种新的变换分析方法，继承和发展了短时傅立叶变换局部化的思想，克服了傅立叶变换容易丢掉时间信息及不利于分析非平稳信号等缺点，能够提供一个随频率改变的时间-频率窗口，实现时间(空间)频率的局部分析，主要特点是通过变换能够充分突出某些方面的特征。“小波”就是小区域、长度有限、均值为0的波形，“小”即其具有衰减性，“波”即其具有正负交替的波动性。小波变换通过伸缩平移运算对信号(函数)逐步进行多尺度细化，达到高频处时间细分，低频处频率细分，并自动适应时频信号分析的要求，从而可聚焦到信号的任意细节。

设ψ(t)∈L2(R),其傅立叶变换为Fψ(ω)，若Fψ(ω)满足容许条件：

(1)

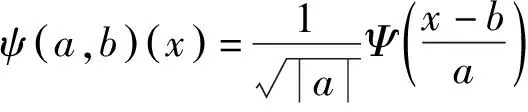
对路面弯沉检测数据等任意的函数或信号f(x)的连续小波变换定义为：

(2)

其逆变换(即回复信号或重构信号)为：

(3)

从定义式可知：连续小波变换实际就是选定一个小波，与处在分析时段部分的信号进行比较，并计算该时刻的连续变换小波系数C，C表示该小波与处在分析时段内的信号波形的相似程度，C越大，两者的波形相似程度越高，然后调整参数a、b，计算出所有尺度的连续小波变换系数，重构信号，即完成了小波变换。

1.2 小波消噪原理

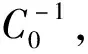
2 弯沉正态化

将路面检测弯沉看作含噪声的信号，利用Matlab中的小波(wavelet)工具箱对其进行消噪处理。经过试验，发现利用Daubecheies(dbN)小波系处理弯沉数据的效果较好，dbN小波的特点是随着阶次(序列N)的增大消失矩阶数越大，光滑性越好，频域的局部化能力越强，频带的划分效果越好，但使时域紧支撑性减弱，并大大增加计算量，实时性变差，较多地改变了原信号的特征；同时，变换等级越大对原始信号中的有用信息破坏越大。因此选用小波函数db2，变换等级选用1级进行路面弯沉数据分析。从8条高速公路检测到的路面弯沉数据中随机挑选60组数据进行路面弯沉正态化分析，组距划分与路面管理系统(CPMS)的路段划分一致，所有数据皆已进行季节、温度影响修正。路面弯沉正态化处理方式有小波消噪、3倍标准差法(以下简称3S法)、2倍标准差法(以下简称2S法)等，采用Shapiro-Wilk检验法检验路面弯沉数据是否服从正态分布。路面弯沉正态化分析结果见表1。

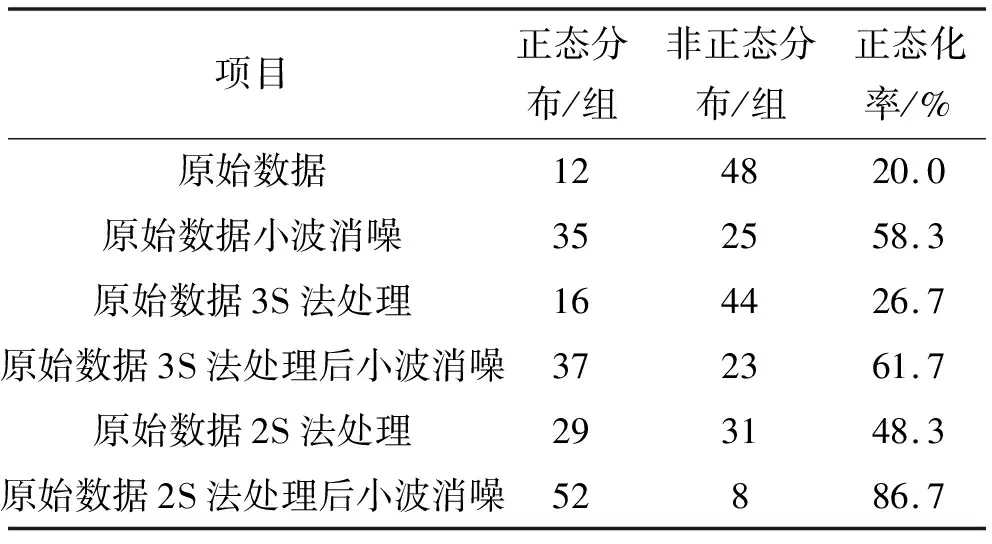
表1 路面弯沉正态化分析结果

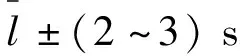
在路面技术状况评定过程中，如果每组数据都进行小波变换，势必非常麻烦，且影响数据处理效率，因此有必要建立处理前后数据间的联系，以减小计算量。将经2S法处理，再经小波变换处理后服从正态分布的数据进行对比，结果见表2、3及图1、2。

从表2、图1可以看出：经2S法处理后的路面弯沉原始数据再经小波变换消噪后，其平均值几乎没有变化，即小波变换完整地保留了路面弯沉的原始特征，说明这种变换是合理且有效的，两者的转换关系为：y=1.001 7x-0.017 2(R2=0.999 7)，其中x、y分别为2S法处理后、小波变换后的路面弯沉平均值。同样，小波变换前后路面弯沉标准差也有良好的对应关系，两者的转换关系为：y=0.785 6x-0.237 7(R2=0.907 9)，其中x、y分别为2S法处理后、小波变换后的路面弯沉标准差。

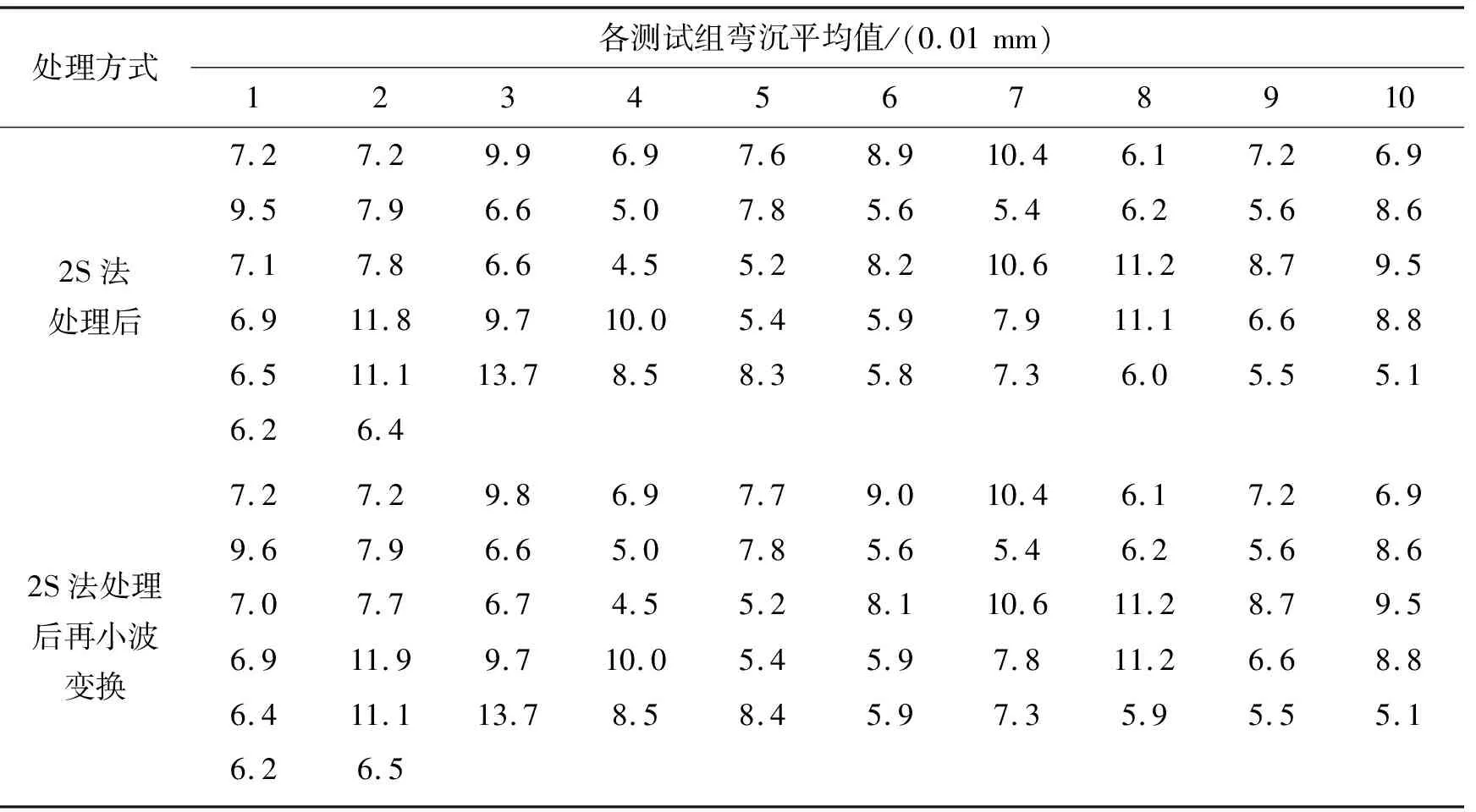
表2 路面弯沉平均值(0.01 mm)

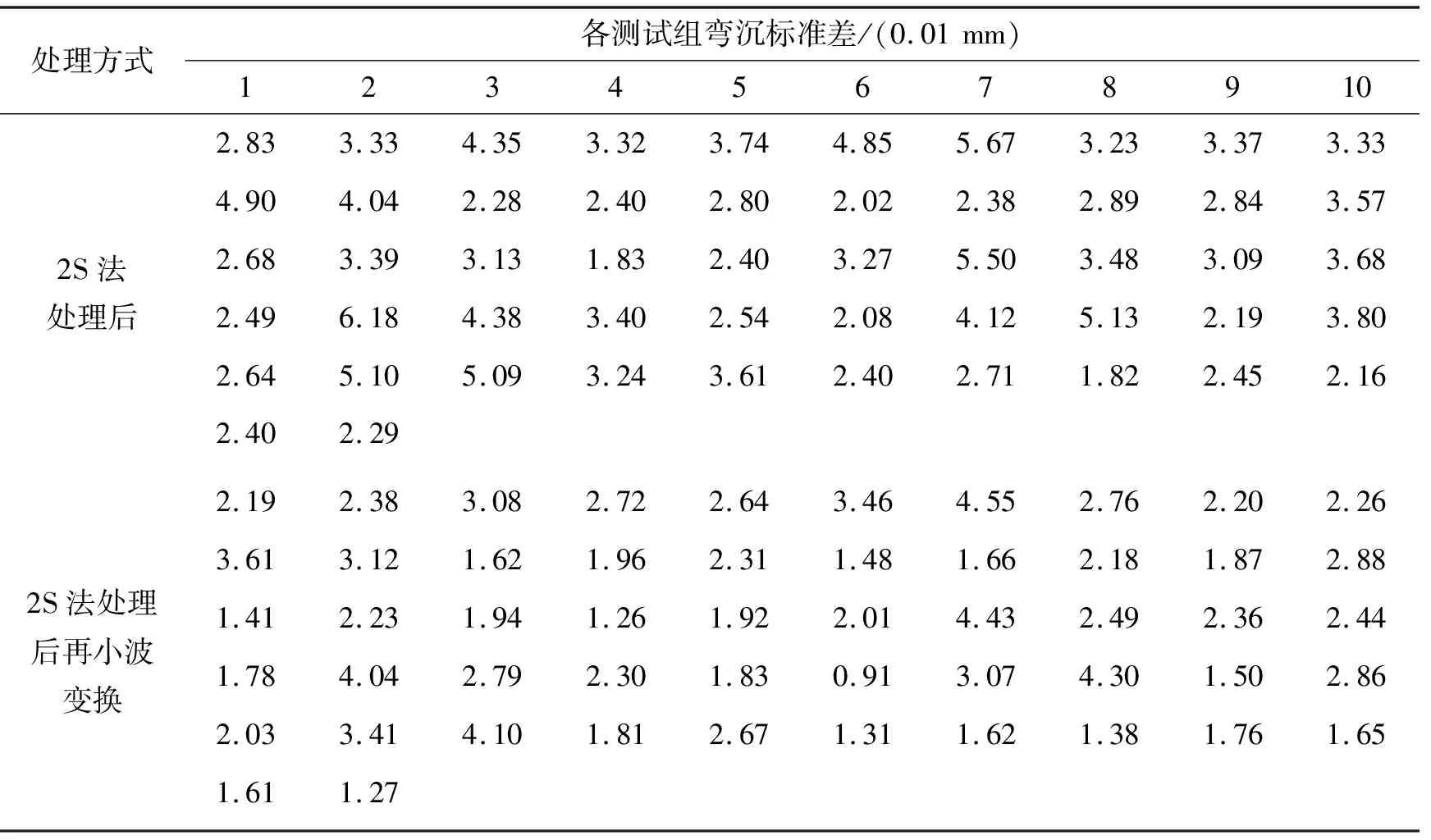
表3 路面弯沉标准差(0.01 mm)

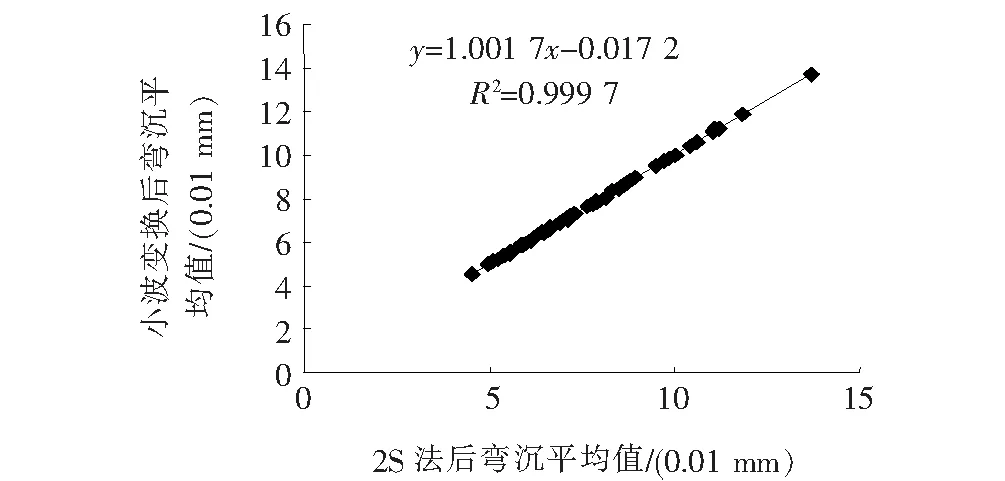
图1 小波变换前后路面弯沉平均值关系图

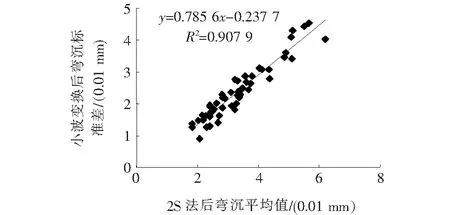
图2 小波变换前后路面弯沉标准差关系图

上述分析表明：路面弯沉原始数据经2S法处理后再进行小波变换，不但能使弯沉服从正态分布，并能保持其原始特征，且小波变换前后的弯沉平均值、标准差存在良好的线性关系，因此可以利用这种关系式代表小波变换对原始数据进行正态化处理。

3 弯沉代表值新的计算方法

基于小波变换对路面弯沉正态化率的良好效果，提出了新的弯沉代表值计算方法，其推导步骤如下：

(1)对路面弯沉数据进行温度、季节系数影响修正，并按路面管理系统路段进行分组。

(2)采用2倍标准差法剔除各组弯沉数据中的特异值。

(3)采用Matlab中的小波函数db2、1级变换等级对经第(2)步处理后的弯沉数据进行小波变换消噪，使弯沉数据服从正态分布。

(4)计算路面弯沉平均值、标准差，建立由第(2)、(3)步处理后的弯沉平均值、标准差的关系式：y=1.001 7x-0.017 2(R2=0.999 7)，式中x、y分别为经第(2)步、第(3)步处理后的弯沉平均值；y=0.785 6x-0.237 7(R2=0.907 9)，式中x、y分别为经第2步、第3步处理后的弯沉标准差。

(5)基于小波变换完整地保留了弯沉的原始特征及良好的正态化转换率，提出新的路面弯沉代表值计算方法，表达式如式(4)所示：

(4)

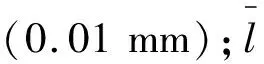
新的弯沉代表值计算法可直接用来计算路面弯沉代表值，取代了对弯沉数据进行小波变换的工作，提高了计算效率。

4 实体工程应用

应用新的弯沉代表值计算公式对某高速公路技术状况进行评定，该高速公路于2004年建成通车，运营期间进行了路面微表处、novachip、罩面等养护处理，路面结构见表4。由于路面结构强度为抽样评定指标，单独计算与评定，故此次公路技术状况评定仅涉及路面结构强度。路面结构强度指数PSSI评定等级统计结果见表5。

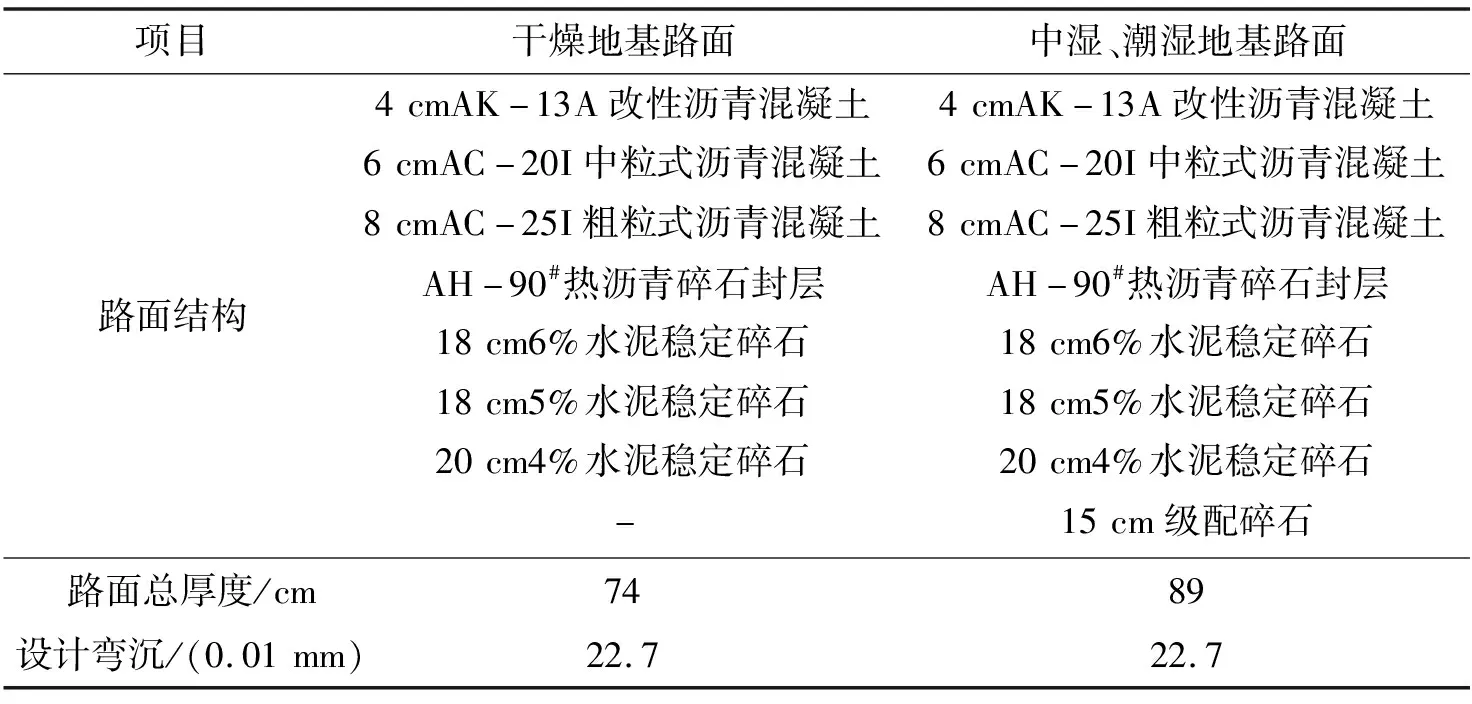
表4 某高速公路路面结构

表5 路面PSSI评定等级对比

表5表明：规范中弯沉代表值算法计算得到的SSI较小，新弯沉代表值算法算得的SSI较大，即按规范评定的路面结构强度较差，而用新的弯沉代表值算法评定的路面结构强度较好，说明采用小波变换对路面弯沉处理后降低了各种因素对弯沉值的影响，路面结构强度指标更能反映路面实际状况。

5 结论

(1)从路面直接采集的弯沉数据正态率很低，不能按规范中的方法计算弯沉代表值，采用3倍及2倍标准差法剔除特异值后，弯沉正态率仍较低，也不能直接计算，采用2倍标准差法剔除弯沉特异值后，再进行小波变换消噪，小波变换消噪前后，弯沉平均值、标准差具有良好的线性相关性，前者相关系数R2为0.999 7，后者相关系数R2为0.907 9，完整地保留了路面弯沉的原始特征，正态化率达到86.7%，且能使非正态数据组正态化率达80.6%，正态组正态化率达93.1%，基本满足规范公式计算的要求。

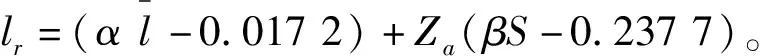
(3)小波变换消噪降低了各种因素对弯沉值的影响，在公路技术状况评定中采用新的弯沉计算公式得到的SSI值比规范推荐的公式计算值大，评定的路面状况更优良，路面结构指标更能反映路面实际状况。