基于灰色理论的沥青路面裂缝预测模型研究

潘旺，严世涛,2，李双蓓,3*

(1.广西大学 土木建筑工程学院，广西 南宁 530004；2.崇左高速公路运营有限公司；3.广西大学 工程防灾与结构安全教育部重点实验室)

1 前言

路面裂缝是沥青路面最常见、发生频次最高的病害。路面裂缝的主要表现形式有横向裂缝、纵向裂缝、龟裂、网裂等，按其成因可分为反射裂缝、温度裂缝和疲劳裂缝。在行车荷载、温度荷载、降雨影响等因素复合作用下，路面裂缝将发展为坑槽、松散等更为严重的路面病害，将加大公路养护难度，提高养护成本，对行车安全性、舒适性及路基稳定性都有较大的影响。因此，建立预测路面裂缝发展的数学模型，对于准确把握路面使用状况，科学预判养护时机并做出科学养护决策具有重要的指导意义。

沥青路面使用性能预测方法目前主要有经验模型、力学模型、人工神经网络以及灰色理论等方法。经验模型不需要复杂的求解，但该方法不能反映数据的变化规律，随着预测时间的增加误差会不断累加；力学模型精度较高，但需要进行大量室内试验和复杂的计算，预测成本较高。灰色系统理论由邓聚龙在1993年首次提出后，在工业、农业、交通、生命科学等众多领域得到了成功应用。2000年以后国内外学者逐渐将灰色系统理论等各种新兴理论运用到路面养护管理领域中。其中灰色系统理论是利用“小样本”、“贫信息”，即通过部分已知信息，就可建立反映系统发展规律的数学模型来预测事物的发展。Wang等将灰色模型运用到路面平整度预测中，但其模型只是从已有的检测数据出发，没有考虑未来可能影响数据趋势的因素；杜二鹏等采用灰色系统理论方法，分别对路面强度指数、路面状况指数和路面平整度指标建立了灰色系统GM(1,1)模型并进行预测；吴栋在灰色模型基础上建立了指数形式的路面性能衰变模型并对某路面衰变情况进行了预测，取得了良好的结果。尽管灰色模型已被广泛应用于路面性能预测，但传统的灰色模型存在着对长期数据预测效果不佳的缺陷。

张洪伟通过不断删除老旧信息和添加新信息，建立了动态等维递补GM(1,1)模型，但其在更新信息中仍有可能删除掉有用信息；金年生将灰色模型和马尔可夫理论相结合，建立组合预测模型，对路面性能衰变规律进行预测，取得了良好的效果；赵静提出了基于灰色关联度分析和支持向量机回归(GRA-SVR)的沥青路面使用性能预测模型。上述模型操作起来较为复杂，路面养护周期不需太长，普通模型即可满足。

综上所述，目前路面灰色系统理论研究多集中在建立单一因素灰色模型进行路况指标分析，对多关联因素的影响考虑较少，考虑气象、车辆等多因素影响下路面性能灰色理论研究也未见报道。该文通过对GM(1,N)模型参数及计算公式进行讨论和改进，建立了改进的灰色模型。为了验证模型的可靠性，选取华南地区湿热环境下一典型路段进行长达6年的现场监测，并对其影响裂缝的相关因素进行分析。根据2013—2017年监测数据建立了路面裂缝预测模型，取得了良好的预测结果。最后基于裂缝率与综合破损率的相关关系，并结合实际道路养护经验，提出养护对策决策树，对于同处华南湿热环境下的广东、广西、海南等地区沥青路面养护均有良好的借鉴价值。

2 灰色系统GM(1，N)模型原理

2.1 灰色模型原理

灰色系统分析方法通过鉴别系统因素之间发展趋势的相似或相异程度，进行关联度分析，寻求系统变动的规律，由此生成数据序列，可用于预测事物未来的发展趋势和未来状态。

GM(1，N)模型表示1阶的N个变量的微分方程预测模型。其中，每个变量含有m个元素，表达式如下：

(i=1,2,…,N)

(1)

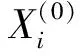
(i=1,2,…,N)

(2)

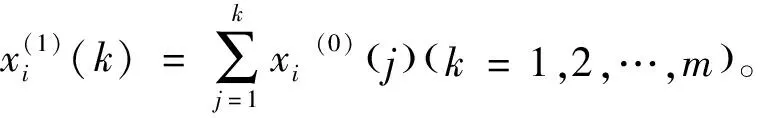
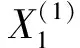
(3)

式中：

(0≤θ≤1，g=2,3,…,m)

(4)

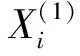
(5)

式中:α，β2，β3，…，βN均为待定参数。

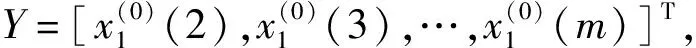
(6)

式中:

(7)

利用最小二乘法，求解式(6)可得出参数列为：

(8)

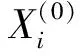
(9)

求解上式可得：

(10)

(11)

2.2 灰色模型改进

灰色预测模型参数采用式(4)进行计算，式中，参数值θ取为：

(12)

将式(8)解出的参数α代入式(12)，重新计算修正参数θ，并记为θ(k+1)。比较θ(k)与θ(k+1)的值，当其差值大于预先给定的阈值，说明θ(k+1)还需要调整，则用θ(k+1)代替θ(k)代入式(4)，重新计算参数序列，再次计算灰色预测模型参数α，β2，β3，…，βN；否则，迭代结束，输出灰色预测模型参数α，β2，β3，…，βN。

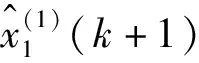
(13)

当j=k时，上式可化简为：

(14)

3 应用灰色模型的路面裂缝预测

3.1 路面裂缝影响因素选取

影响路面裂缝的因素较多，但在相关研究领域中并未形成公认的可供直接阐述的影响指标。为了确定不同因素对路面裂缝的影响，2013—2017年，笔者对南友高速公路K73+000～K87+000及K192+000～K209+000两段典型路段进行了路面裂缝监测。监测措施以人工巡检为主、路况检测车与探地雷达为辅，按月定期采集路面裂缝数量、长度、扩展量等数据。南友高速公路处于华南地区典型湿热环境影响下，其中车辆荷载通过车流量折算为标准车当量数来表征，选取2017年车辆数当量、新增裂缝长度、数量及总长等监测数据绘制如图1～4所示变化曲线。

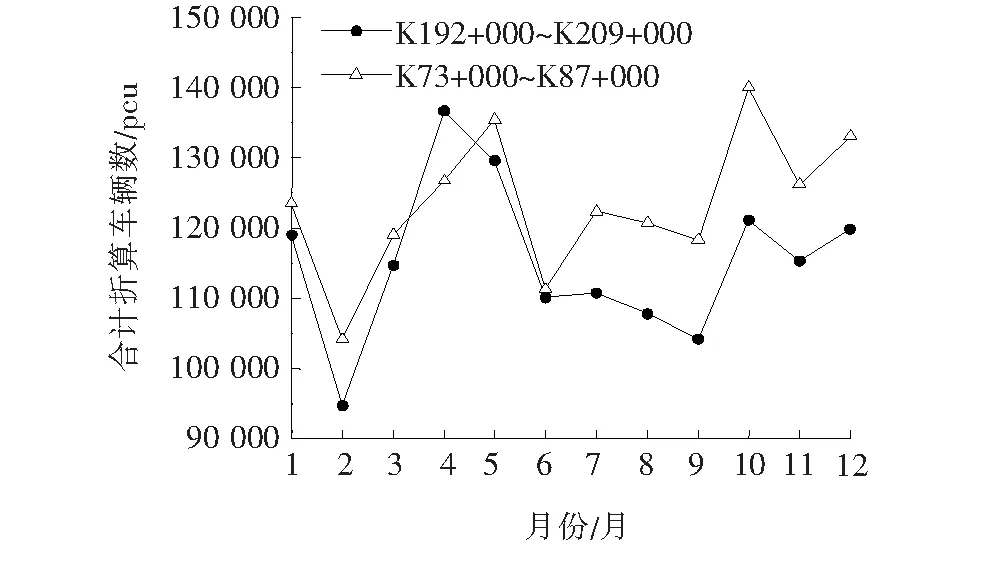
图1 2017年每月合计折算车辆数

由图2可知：全年裂缝平均长度均在2～4 m范围内波动，其数值并没有随着季节更替而发生规律性的变化。由图3可以看出：K192+000～K209+000段新增裂缝数量在1～12月份中，呈现先增加再减少再增加的趋势，其数值在9、10月份达到峰值。由图4可得：裂缝总长的改变规则与图3中裂缝数量的改变规则基本类似。两个路段的裂缝总长与数量的改变规则基本类似，其峰值点在5、10及11月份。

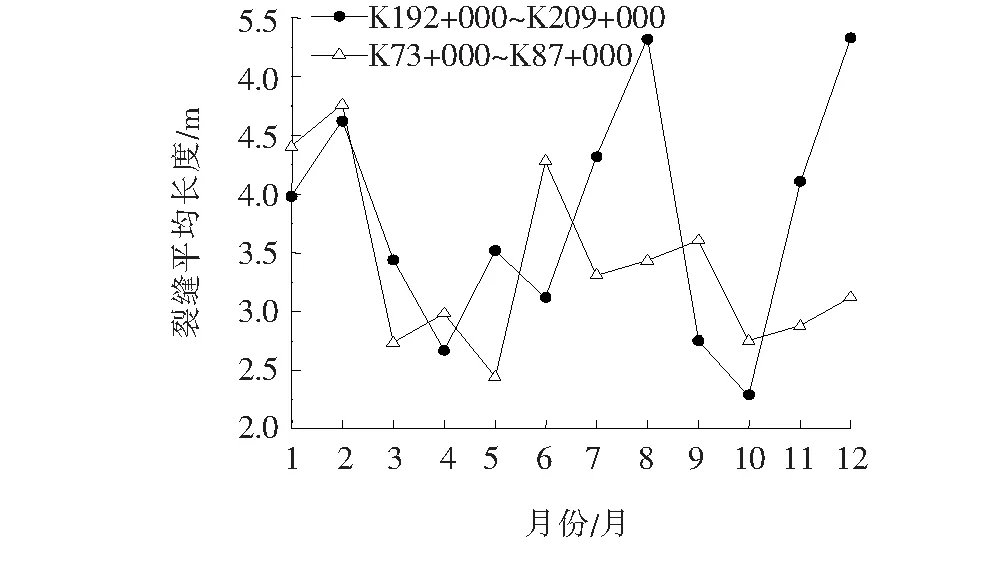
图2 2017年每月新增裂缝平均长度

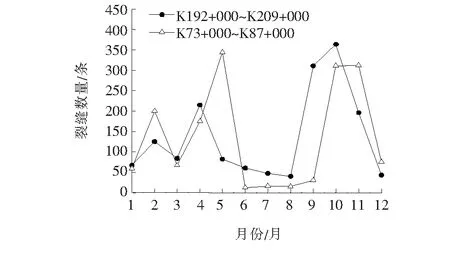
图3 2017年每月新增裂缝数量

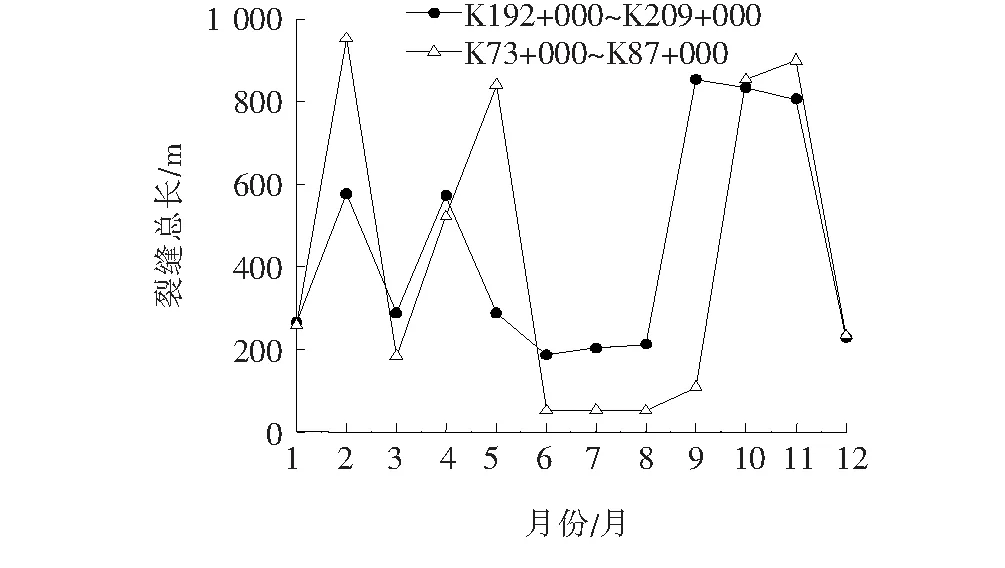
图4 2017年每月新增裂缝总长

监测路段自2013年实施全线罩面后在监测时间内均没有进行大修和中修，造成在不同月份内，裂缝病害情况不同的主要原因是车流量及气候因素。通过查询当地气候条件可以看到，该路段处于南亚热带西部气候区，全年夏长冬短，降雨丰富。9、10及11月均为当年出现温度大幅变化频次较高的月份，且月降雨量均为150 mm以上，大量的降雨通过路面裂缝渗透到土基，在行车荷载和水温耦合作用下路面很容易产生结构性破坏，裂缝扩展速率及扩展数量快速增大。综合考虑道路养护需求及道路使用折损以及数据无量纲化处理等情况，该文选取合计折算车辆数、年降雨量、月均温度方差以及使用年限作为建立路面裂缝预测模型的相关因素。

3.2 GM模型建立

根据上述因素分析，该文对南友高速公路K198+000～K208+000路段裂缝监测数据进行整理，监测数据见表1。所需的气象参数引用“中国气象科学数据共享服务网(http://cdc.cma.gov.cn)”所提供的广西凭祥站点的数据，其精度可达每小时记录1次。

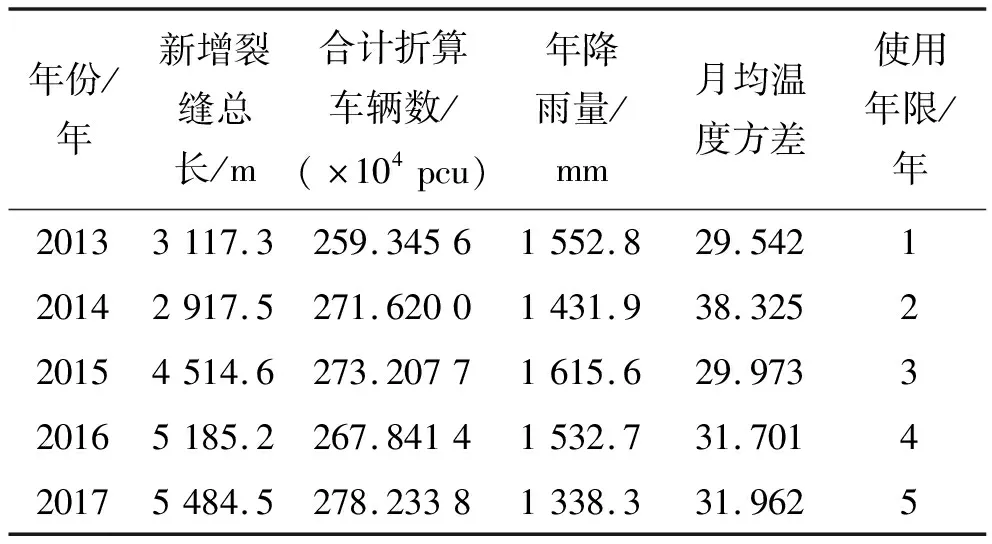
表1 南友高速公路K198+000～K208+000段预测模型参数

B=

7.000 3，100.160 7，2 781.724 6]T

分别以θ(1)=0.3和θ*(1)=0.8为初始值代入式(4)中，进行迭代计算，得到如下计算结果：

[θ(1)，θ(2)，θ(3)，θ(4)，θ(5)，θ(6)，θ(7)]≈

[0.3，0.351，0.404，0.560，0.532，0.501，0.502]

[θ*(1)，θ*(2)，θ*(3)，θ*(4)，θ*(5)，θ*(6)，θ*(7)]≈[0.8，0.425，0.431，0.457，0.489，0.503，0.501]

可以看出，随着迭代步数的增加，参数值θ逐渐收敛于0.5。在迭代过程中对应的各年度预测值如图5所示。

由图5可知：在初始迭代步中，预测值与真实值误差较大，随着迭代次数的增加，模型预测值逐渐逼近真实值。两种迭代过程都经历了前3步迭代结果的剧烈变化，而后每次迭代结果均以相对均匀的误差平稳地逐渐逼近真实值。尽管初始参数θ取值不同，但最终θ都趋近于同一数值，且迭代步数也相同。说明对于不同灰色模型，都有其预测结果最为准确的参数θ取值，通过对θ值进行调整迭代，可以提高灰色模型预测精度。该文选取θ=0.5能够较好地反映前后初始值计算中的权重关系，误差较小。

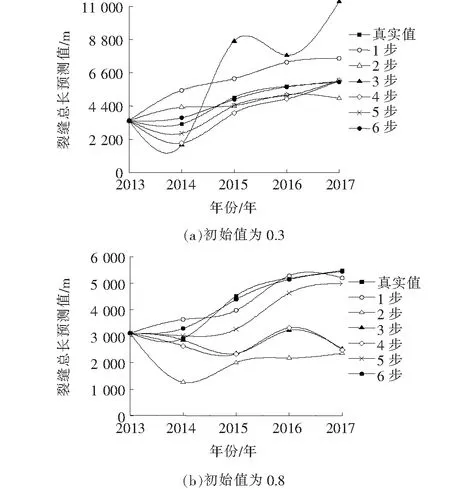
图5 迭代过程中裂缝总长预测值

对应θ=0.5，得到2013—2017年5年新增裂缝总长预测结果分别为:

3.3 模型误差分析

(1)残差检验

(15)

可得：

ε0(2)≈-374.67，ε0(3)≈124.25，ε0(4)≈43.35，ε0(5)≈40.73。

(2)相对误差检验

(16)

求得:

Δ2≈11.94%，Δ3≈4.19%，Δ4≈0.83%，Δ5≈0.74%。

表明该文提出的改进灰色模型对路面裂缝预测问题的求解精度较高。

根据该模型可进一步得到2018—2020年间裂缝发展情况。首先得到3年合计折算车辆数、年降雨量(mm)、月均温度平方差分别为:

[2 763 453，2 778 085，2 792 794]T

将上述结果代入GM(1，N)模型得到2018—2020年3年的路面新增裂缝总长的预测值分别为：

[6 367.92，7 271.78，8 303.94]T

3.4 灰色模型与传统预测模型对比分析

该文分别采用传统回归模型、传统灰色模型与该文提出的改进灰色模型对以上算例进行建模，给出了不同方法的裂缝预测结果，将其与实测值进行对比，结果见表2。

表2 改进的灰色模型与传统预测模型对比分析

由表2可以看出：传统回归模型仅以离散点到回归点的总方差最小为目标，未考虑数据内部及数据与相关数据之间的内在联系，对于离散性较大的数据拟合效果较差。传统的灰色模型引入了数据之间的灰色关联信息，比较真实地反映了数据的发展趋势。该文提出的改进灰色模型，对数据的处理采用了一种固定有效数据容量的方法，随着预测步的迭代，对用于预测的数据进行更新，减小旧数据对预测结果的干扰，降低了数据离散程度，保证了预测结果的收敛性。对于该文提出的路面裂缝预测问题，改进的灰色模型在每步进行预测分析时，仅需前5年的相关数据，即可达到较高的预测精度，同时也提高了计算效率。

4 裂缝率分析

在现行的公路管理规范中，是通过路面综合破损率(DR)和路面破损状况指数(PCI)来评价路面损坏状态的。路面裂缝率(DRc)可以直接通过自动化监测设备获得，相比于路面综合破损率(DR)和路面破损状况指数(PCI)的获取更加简便、高效。此处通过分析DRc与DR和PCI之间的相关性，结合实际道路养护经验，提出考虑DRc的沥青路面养护对策决策树。

4.1 裂缝率计算

由JTG D50-2017《公路沥青路面设计规范》中PCI及DRc的定义可得：

PCI=100-α0DRα1

(17)

式中：对于沥青路面，α0取15，α1取0.412。

DRc=100Nc/N

(18)

式中：Nc和N分别为路面裂缝(坑槽)影响面积和监测的路面面积(m2)。

将现场监测得到的数据代入式(17)、(18)，可得南友高速公路K198+000～K208+000段2013—2017年5年的DRc与DR关系如图6所示。

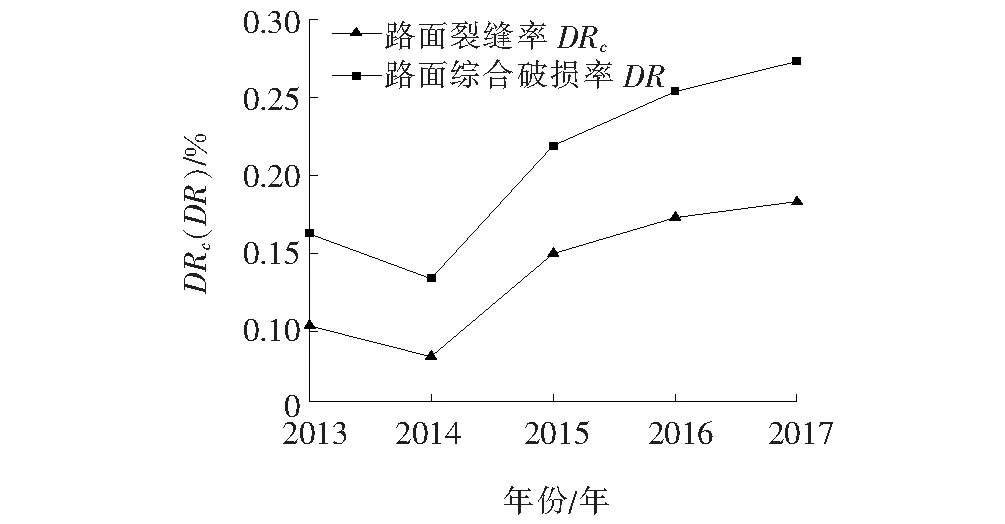
图6 DRc-DR关系图

Pearson线性相关性分析常用来定量描述两个定量变量间直线相关的方向和密切程度，具有较高的精确度。该处采用Pearson分析方法对现场监测得到的数据进行相关性分析，结果表明监测路段DRc与DR、PCI在0.01的水平下，相关性达到了99.8%，线性相关性显著。

4.2 由裂缝率快速编制路面预防性养护方案

根据DRc与PCI之间的关系，结合以往的养护方案与实际道路养护经验，采用DRc代替PCI的方法，综合考虑路面裂缝率、车辙、路面平整度3项指标，建立相应的路面裂缝病害预防养护对策决策树见图7。该决策树可作为辅助养护从业人员快速编制中短期养护计划的有效方法。

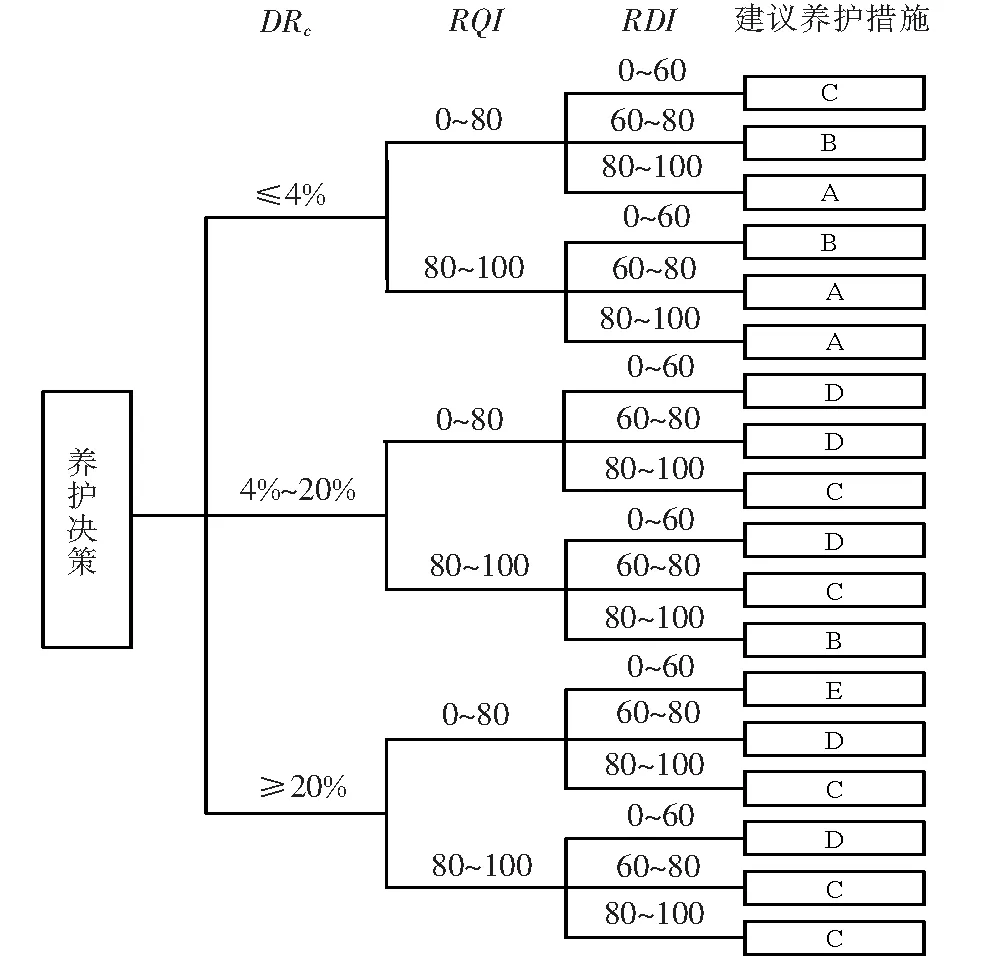
注：养护措施：A-日常养护与小修；B-中修罩面；C-中修加铺抗滑层；D-大修重建；E-大修补强。

5 结论

(1)基于自适应的数据更新方法对灰色模型进行了改进，改进的灰色模型较常规灰色模型具有误差小、精度高、收敛快等优点，有效地减小了老数据对较远时刻预测值的影响。参数值θ的取值对预测结果有较大影响，在应用中与初始数列相邻值之间的关系有关，通过对θ值的试算迭代，模型预测值收敛于真实值。

(2)对于GM(1，N)模型，选取的相关因素越多对预测模型的准确性影响越大。该文首先对灰色模型预测影响因素进行分析，综合考虑选取合计折算车辆数、年降雨量、月均温度方差以及使用年限作为建立路面裂缝预测模型的相关因素。

(3)考虑监测路段在监测周期内车辆数、降雨量、温差以及使用年限等相关因素，建立了年度新增裂缝的GM(1，N)预测模型，并据此预测了未来3年路面新增裂缝总长。与传统预测模型进行对比可知，该文提出的改进灰色系统理论GM(1，N)模型具有预测精度高、更能体现出离散数据之间的隐含关系的优势，为准确预测道路裂缝发生，进而科学评判道路技术状况提供重要依据。建立的预测模型也可应用于其他类型路面病害的预测中。

(4)分析了路面裂缝率(DRc)与路面综合破损率(DR)及路面破损状况指数(PCI)之间的相关性，结合实际道路养护工程经验，提出了根据DRc而采取的相应养护对策决策树，对实际道路施工、养护具有一定的指导作用。其方法对于同处华南湿热环境下的广东、广西、海南等地区沥青路面养护均有良好的借鉴意义。