基于改进自适应遗传算法和二维最大熵的超声红外热像缺陷识别

唐长明,钟剑锋,钟舜聪,2,陈 曼,伏喜斌,黄学斌

(1.福州大学 机械工程及自动化学院光学/太赫兹及无损检测实验室，福建 福州 350108;2.上海大学 机电工程及自动化学院，上海 200444;3.厦门市特种设备检验检测院，福建 厦门 361000)

0 引言

超声红外技术是一项将超声波技术和红外技术相结合的新兴无损检测技术，它对结构件的表面裂纹、近表面裂纹、分层和脱粘等界面类缺陷具有良好的检测效果。相比于其他激励方式的红外热成像技术，超声红外热像法是采用超声波作为激励源，因其激励强度大、作用时间短，从而具有检测速度快，能实现大面积检测的优势，并且无需对检测对象进行表面预处理[1-3]。该检测法是利用超声波在缺陷处的衰减生热来检测裂纹，能够在缺陷处选择性加热，增强了检测图像的信噪比，提高了检测的灵敏度，适用于形状结构复杂无规则、大重量级的检测对象[4-5]。在实验过程中由于背景噪声、材料不均匀等因素使得红外热像仪采集到的热像图存在成分复杂、噪声严重、边缘模糊等缺点[6]，易造成对缺陷的误判，同时为了进一步将超声红外无损检测推向工程应用，需要实现缺陷的自动识别。

鉴于此，本文提出一种对超声激励作用下的红外图像实现自动检测的方法，采用图像差分运算和形态学开运算对图像进行去噪，结合改进的自适应遗传算法和二维最大熵对图像进行阈值分割，提取缺陷区域，并进一步利用连通区域标记实现缺陷位置的提取。

1 二维最大熵图像分割法

由于一维最大熵分割方法只考虑自身像素点而没有考虑邻域像素点的信息，当图像的对比度低、背景噪声严重时，灰度直方图不一定有波峰和波谷，此时利用一维最大熵法方法进行阈值分割效果不好，目标区域和背景区域不能很好地区分开。为此，一些学者提出了二维最大熵阈值分割的方法，该方法是一种结合本身像素点灰度信息和邻域灰度值信息的阈值分割方法[6-7]。

假设一张大小为MXN，具有L级灰度值红外图像的二维直方图的xoy平面图如图1所示。图中横坐标为原图像f(i,j)的灰度级，纵坐标为对原图像经过平滑处理后求得的图像g(i,j)的灰度级，区域1、2 代表的是目标区域和背景区域，区域3、4 代表的是噪声和边界。二维最大熵分割方法是通过选取一定的阈值(s,t)，使得区域1 和区域2 的熵之和为最大值。

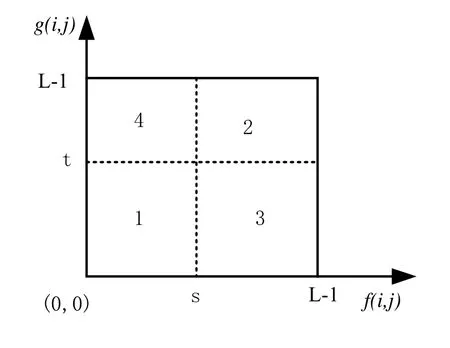
图1 二维直方图投影图Fig.1 Two-dimensional histogram projection

图像的二维直方图可由公式(1)计算得出:

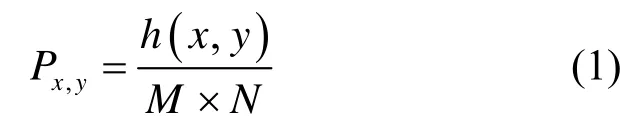
式中:h(x,y)为原图像中灰度值为x、且邻域平均灰度值为y的像素点的个数;M和N分别为图像的横向、纵向分辨率。假设分割的阈值选为(s,t)，则红外图像中目标区域1 和背景区域2 的概率分别为:

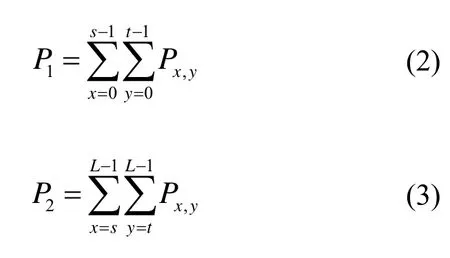
则红外图像中目标区域1 和背景区域2 的熵分别为:

将红外图像的二维熵函数H(s,t)定义为:

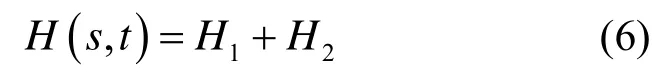
当熵函数H(s,t)取得最大值时，对应的(s*,t*)即为二维最大熵阈值:

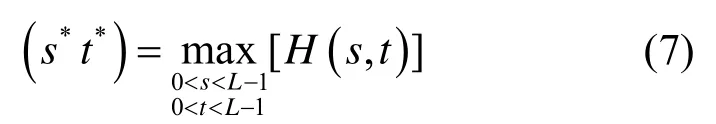
2 改进的自适应遗传算法

遗传算法(Genetic Algorithms,GA)是由Michigan大学的J.Holland 教授提出的一种模拟达尔文生物进化论的寻找全局最优值搜索算法[8-9]。遗传算法是将随机生成几个初始解作为初始群体即第一代，然后初始群体像生物进化一样进行"优胜劣汰"的选择、交叉繁殖、基因变异等，产生生存能力更强、性能更优于子代群体，子代群体又作为新父代产生新的子代群体，如此循环，得到的解越来越靠近最优解[10-11]。

简单遗传算法存在着一些缺点，比如收敛性差、求解速度慢、容易陷入局部最优解。国内外有许多学者针对简单遗传算法的缺点展开了大量的研究，提出了许多不同的改进遗传算法，使遗传算法的性能得到了很大程度的改善，提高了遗传算法的适用性。本文在此基础上，对简单遗传算法中的3 个遗传算子进行改进来提高遗传算法的计算速度和收敛性。

本文算法的基本流程:

1)编码。本文采用的是二进制编码，由于图像的灰度级为256，故每个个体的二进制编码为16 位，前面8 位为原红外图像的阈值s，后面8 位为对原红外图像经过平滑处理后图像的阈值t。

2)生成初始群体。本文采取完全随机的方法在可行解空间生成初始群体。通常种群规模的数量为20～100，本文的种群规模设定为20。

3)适应度函数。本文采取的适应度函数为红外图像的二维熵函数。

4)遗传算子。本文的选择算子同时结合轮盘赌选择法和最优个体保留。本文算法采取10%的最优个体保留的方法，即每次进行轮盘赌选择前，先从20 个群体中选择2 个最优个体无条件复制进入下一步操作。

在简单遗传算法中，交叉率Pc与变异率Pm均是采用固定值，这使得取值较为困难，若取值太大在算法后期会破坏优秀个体，太小则使得算法前期搜索能力较差[12]。针对此问题，SRINVIVAS 等人曾提出了一种交叉率Pc和变异率Pm随着种群进化而自动调整的自适应基本遗传算法。该算法的交叉率Pc和变异率Pm的调整如式(8)和式(9)所示[13]:

式中:k1、k2、k3、k4为常数，值域为(0,1);fmax当代群体中的最大适应度值;favg为当代群体平均适应度值;f′为当代待交叉染色体对中的较大适应值;f为待变异个体的适应度值。

从上述两个公式可以看出，该算法的交叉率Pc和变异率Pm随着种群的进化而变小，可以提高收敛速度。但是，该算法存在着不足，当待交叉个体或者待变异个体的适应度值很接近或者等于群体中最大适应度值时，交叉率Pc和变异率Pm直接等于0，这种情况要是发生在算法早期的局部最优个体上，会使算法收敛于具有最优解，形成伪解。因此，本文在此基础上，采用改进的算子，即使在算法几乎收敛的时候，交叉率Pc和变异率Pm仍然不为0，该算子如式(10)和式(11)所示:

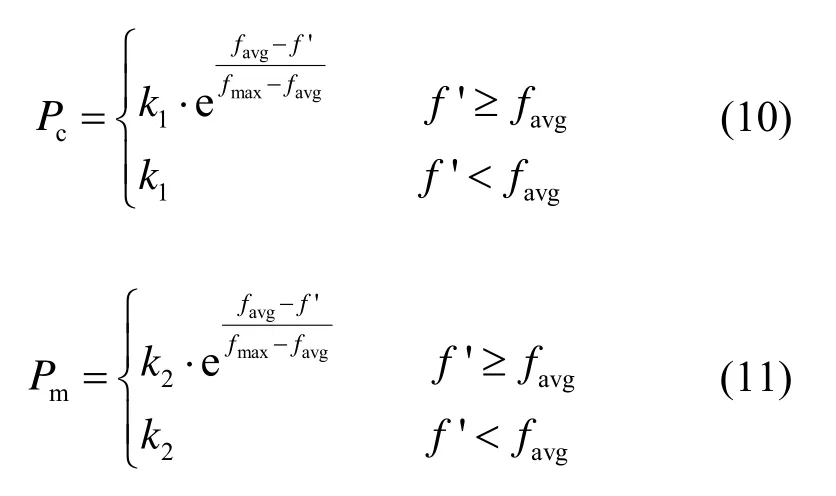
式中:k1为最大变异率，在本算法中将其取为0.9;k2为最大变异率，在本算法中将其取为0.1。从式中可以看出，经过改进的算子在算法的初始阶段交叉率Pc和变异率Pm都取较大值，提高算法的搜索性能，加快搜索速度，同时在算法的后期阶段，适当地降低交叉率Pc和变异率Pm防止过度破坏最优个体，加快收敛，此时的交叉率Pc和变异率Pm并不为0，不会陷入局部最优解。

5)迭代终止条件。本算法的终止条件为:当算法达到最大迭代次数时终止，本算法的最大迭代次数为200;或者当子代的群体平均适应度与上一代群体的平均适应度的差小于0.001 同时子代个体中的最大适应度不等于0 时算法终止。由于实验得到的图像经过预处理后，图像中大部分的区域都是属于低灰度级，为了防止算法在初始几代中出现连续两代群体的适应度值全部为0 而导致终止，故采取当子代个体中最大适应度不等于0 时方可终止迭代。

本文的图像分割算法流程图如图2所示。

3 实验与分析

3.1 试件的渗透检测

本文实验利用超声红外热像技术检测奥氏体不锈钢焊缝裂纹，焊缝裂纹是通过焊接工艺在焊缝上随机产生的表面裂纹。为了验证后续实验的正确性，首先对实验试件进行渗透检测，以确定裂纹的数量及位置，渗透检测结果如图3所示。

3.2 图像预处理

本研究选取在超声波激励幅值A=32 μm、激励频率f=20 kHz、激励时间t=2 s 实验条件下的热波序列图为例进行图像处理。该实验的红外热波序列图如图4所示。由于奥氏体不锈钢试件反射率高、采集设备、操作等原因，导致采集到的实验图像具有一定背景噪声。本文首先利用多图像平均法对序列图处理得到平均图像，再将平均图像减去初始图像去背景噪声。

图2 图像分割流程图Fig.2 Image segmentation flow chart

在差分运算后得到的图像中，一些比较明显的、具有干扰性的背景噪声被较好地抑制，但是仍然存在着一些由试件高频振动引起的细微干扰信号，为此，本文采用形态学开运算去除细微的干扰信号。图像预处理过程如图5所示。

3.3 图像分割

对预处理后的图像进行分割，利用本文的分割方法进行分割的结果如图6所示。

从图中可以看出，尽管由于热的传播使得裂纹区域面积比实际情况稍大，但还是能够准确地分割出裂纹区域。从图3的渗透检测实验结果可以看出，2 号裂纹和3 号裂纹两个裂纹之间的间隔非常短，热流的传导使得两个裂纹摩擦生热产生的温度场相互影响形成一个升温区域，故图6中的2 号裂纹和3 号裂纹融合成同一块目标区域了。

为验证本文算法的准确性，本文利用穷举法和简单遗传算法对同一张图像进行分割，分割的结果如图7、图8所示。对比图6可以看出，相比于简单遗传算法，改进的自适应遗传算法分割的结果更接近于穷举法的分割结果，表明了本文算法具有更高的分割精度。

进一步地，本文对该算法的分割速度进行验证，由于遗传算法的分割具有随机性，每次的分割结果和效率都会有细微的差别。因此，本文利用每种算法对同一张图像进行20 次分割，取其平均值，实验数据如表1所示。

从表1中可以看出，基于改进遗传算法的二维最大熵分割速度远远高于穷举法的分割速度，分割时间从54.227 s 降低到0.4115 s;相比简单遗传算法，改进遗传算法的平均运算时间从0.6045 s 缩短到了0.4115 s，降低了31.93%，分割速度也有了明显的改善。

图3 渗透检测结果图Fig.3 Penetration test results

图4 试件表面红外热波序列图(A=32 μm)Fig.4 Infrared heat wave sequence of specimen surface (A=32 μm)

图5 图像预处理Fig.5 Image preprocessing

图6 改进遗传算法分割结果Fig.6 Segmentation result using improved genetic method

图7 穷举法分割结果Fig.7 Segmentation result using exhaustive method

图8 基本遗传算法分割结果Fig.8 Segmentation result using basic genetic algorithm

为了进一步说明本文算法的有效性，本文对在另外两个激励幅值A=24 μm、A=28 μm 激励下的红外热波序列图进行图像处理，激励频率f=20 kHz、激励时间t=2 s，利用本文的算法的分割过程及结果如图9和图10所示。

表1 不同算法的图像分割速度比较Table 1 Segmentation speed of different methods

图9 图像分割结果(A=24 μm)Fig.9 Segmentation result (A=24 μm)

图10 图像分割结果(A=28 μm)Fig.10 Segmentation result (A=28 μm)

从图中可以看出，在两个激励幅值A=24 μm、A=28 μm 激励下的红外热波序列图都可以利用本文的算法进行图像分割，且都能较好地实现对裂纹缺陷区域的提取，完成缺陷区域和背景区域的区分。

3.4 缺陷定位

在图像分割的基础上，本文进一步采用连通区域标记提取出缺陷的位置。本文采用8 邻接方式进行连通区域标记，提取连通区域的个数。然后再求得各个连通区域的质心，利用质心来确定裂纹区域的大致位置。本文对阈值分割后的二值图像进行连通区域标记，如图11所示。将利用连通区域标记提取的缺陷位置与渗透检测得到的缺陷位置进行对比，如表2所示。表中的数值表示缺陷距试件左边缘的水平距离。

图11 连通区域标记图Fig.11 Connected area with marker

表2 不同方法下的裂纹位置对比Table 2 Position of the crack obtained from different method

从表2中可以看出，利用连通区域标记提取的裂纹缺陷位置信息与本文的渗透检测实验结果的裂纹位置信息基本一致，表明了本章提出的红外图像处理方法能够较好地对超声红外实验结果进行处理，实现缺陷的识别与定位，提高超声红外检测方法的缺陷识别率。

4 结论

本文对奥氏体不锈钢焊缝裂纹在超声激励作用下的红外热波序列图进行图像处理，首先利用多图像平均法对红外热波系列图进行处理，将得到的平均图像与序列图中的第一帧初始图像进行图像差分运算去背景，然后用形态学开运算去除由实验试件高频振动引

起的图像漂移而产生的干扰噪声。在此基础上，提出一种结合改进的自适应遗传算法和二维最大熵的图像方法，对预处理后的图像进行分割，提取图像中的裂纹区域。最后，利用连通区域标记提取裂纹区域的位置信息。实验结果表明:利用图像差分运算和形态学开运算相结合的预处理能对超声红外热波序列图较好地去噪;结合改进的自适应遗传算法和二维最大熵的图像分割方法能对图像实现较好地分割，相比于穷举法，它的分割速度有了很大的提高，分割时间从54.227 s 降低到0.4115 s，相比于简单遗传算法，它的分割精度更高，同时分割速度平均提高了31.93%;利用连通区域标记能对缺陷实现准确的定位。