基于JMS-SMC-PHD滤波的检测前跟踪算法

薛秋条,宁巧娇,吴孙勇,2,蔡如华,伍雯雯

(1.桂林电子科技大学 数学与计算科学学院，广西 桂林 541004;2.广西密码学与信息安全重点实验室，广西 桂林 541004)

0 引言

多机动目标跟踪是目标通过在不同的模型之间的转换，利用模型转移概率矩阵来实现的一种方法，因为基于单一模型的跟踪是不能准确预测目标的运动轨迹的[1]。跳跃马尔可夫系统(jump Markov system，JMS)模型是解决机动目标跟踪的有效方法[2-4]。JMS 通过使用多个描述目标运行轨迹的模型并行实现机动目标跟踪。对于多目标的跟踪，Mahler 利用随机有限集理论(random finite sets, RFS)，提出了有限集统计学理论(finite set statistics, FISST)[5]，随后提出了概率假设密度(probability hypothesis density，PHD)滤波[6]。PHD滤波是用一阶统计矩近似后验概率密度函数，该算法将复杂的多目标状态空间运算转化为单目标状态空间运算，有效避免了复杂数据联合问题。国内外学者将PHD、cardinalized probability hypothesis density(CPHD)和Bernoulli 滤波使用点量测与JMS 模型结合，实现对多机动目标的跟踪[7-10]。

检测前跟踪(track before detect，TBD)是解决低信噪比条件下弱小目标检测与跟踪的有效方法[11]。TBD 不用事先设定检测门限对目标有无进行检测，而是直接利用传感器量测数据进行目标跟踪，可以最大限度地保留目标的信息。近年来，国内外学者将TBD技术与随机有限集滤波进行结合，有效地实现对多个弱小目标的检测与跟踪问题[12-14]。对于机动弱小目标的检测与跟踪问题，国内外学者采用多模的随机有限集滤波与TBD 技术进行结合，也能有效地实现[15-16]。本文针对低信噪比条件下机动弱小目标的检测与跟踪问题，提出基于JMS-SMC-PHD 滤波的检测前跟踪算法。该算法以SMC-PHD 滤波为基础，在目标跟踪的预测阶段利用跳跃马尔可夫系统模型实现对目标状态的转移，在权值更新阶段直接使用红外传感器量测数据实现对所有粒子的权值进行更新。最后通过仿真实验证明，所提算法可以有效地实现多个弱小机动目标的检测与跟踪。

1 系统模型

1.1 目标运动模型和量测模型

针对多目标的跟踪问题，假设在k(k=1,2,…)时刻，在观测区域内存在Nk个目标，并用一个随机有限集表示为:

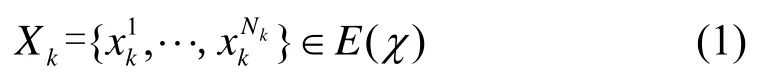
式中:E(χ)为目标状态的所有有限子集。目标的状态集包含目标的存活、新生和衍生部分，k时刻目标s(k=1,2,…,Nk)的运动方程可表示为:

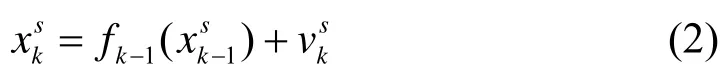
红外传感器以一定的帧频对监视区域进行监测，得到一幅关于监测区域的二维图像，图像包括nXm的感应像元每一个分辨单元对应一个矩形区域ΔxXΔx，且每一分辨单元(i,j)的中心为(iΔx,jΔx)，i=1,…,n，j=1,…,m。则分辨单元(i,j)的观测强度zk(i,j)可以表示为:

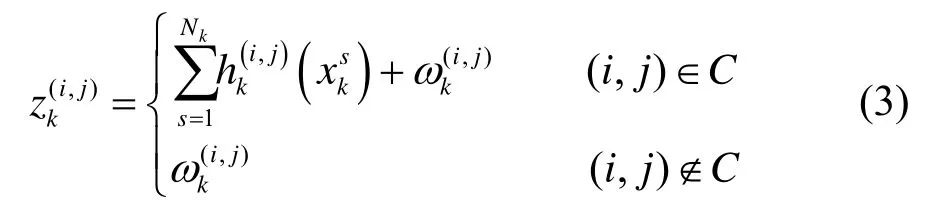
式中:ωk(i,j)为零均值高斯白噪声，即并且各个单元之间是相互独立的。C表示目标扩散影响区域其中为离目标状态xks最近的整数单元。hk(i,j)(xks)为目标xks对分辨单元(i,j)的贡献强度，一般采用点扩散函数的形式:

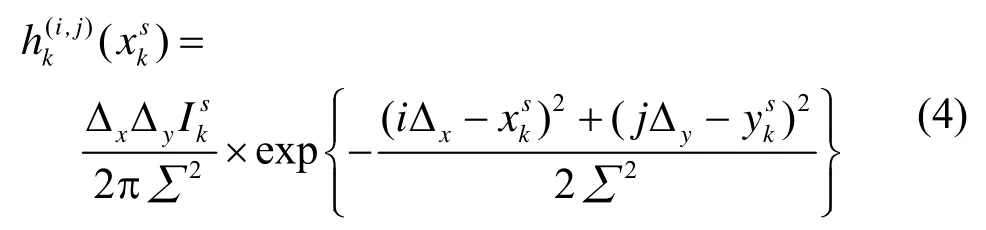
式中:∑为传感器引入的模糊参数，一般是已知的。点扩散函数产生的强度大小以目标xks影响最大单元向周围单元减小，所以目标的影响区域是有限的，在最靠近目标的单元取得最大值。从而k时刻的量测可以表示为:以及从1～k时刻的所有量测数据可以表示为:Z1:k={zl:l=1,…,k}。

1.2 跳跃马尔可夫系统模型

跳跃马尔可夫系统通过一组参数化的状态空间模型去描述，各个状态空间模型之间转移是服从马尔可夫链[5]。JMS 提供了一种不再是通过单一模型的方法去模拟机动目标，是解决机动目标跟踪的有效方法。

k-1 时刻多目标状态随机有限集Xk-1中的目标增广状态(xk-1s,rk-1s)∈E(χ)=RnXN(s=1,…,Nk-1)要么以概率为Ps,k(xk-1s,rk-1s)存活到下一个时刻，要么以概率为1-Ps,k(xk-1s,rk-1s)死亡，其中xk-1s∈Rn和rk-1s∈N分别表示k-1 时刻运动状态和模型标签，N为所有模型标签组成的离散集。模型转移概率是服从离散马尔可夫链，且存活目标状态从k-1 时刻转移到k时刻的转移密度为:所以对于增广状态向量(xks,rks)的转移概率可表示为:

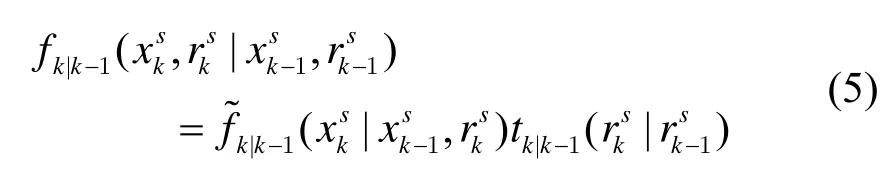
红外传感器量测的似然函数可表示为:

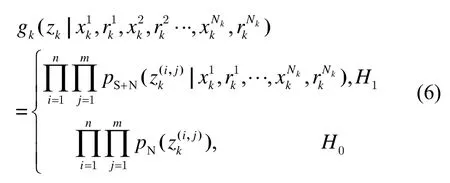
式中:H1表示存在Nk个目标，H0表示不存在目标。pN(zk(i,j))表示分辨单元(i,j)处背景噪声的概率密度函数，则表示目标加噪声的概率密度函数。对于高斯背景噪声条件下，上式可以表示为:

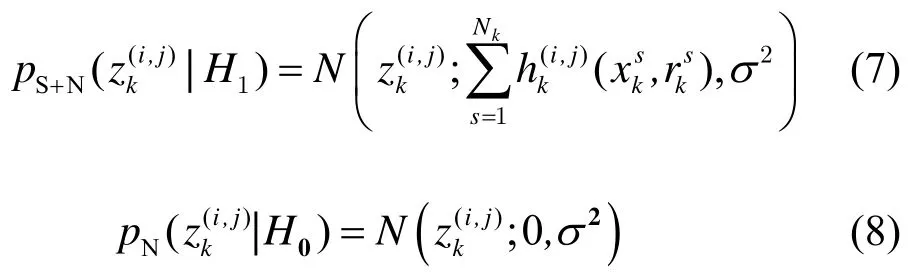
由于目标影响区域是有限仅能对其所在单元和邻近区域有显著影响，因此似然函数可进一步描述为:

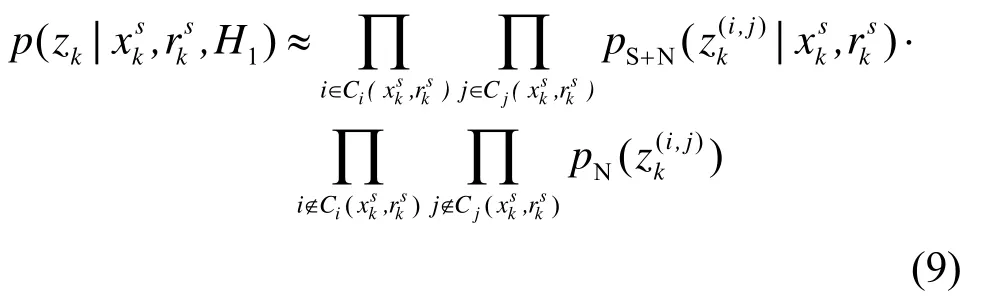
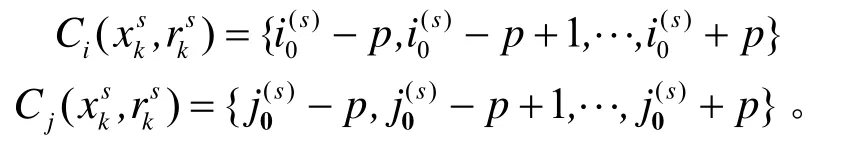
2 基于JMS-SMC-PHD 滤波的TBD 算法

根据贝叶斯理论，滤波的实现可以分为预测阶段和更新阶段，预测是实现目标状态的转移，更新则是在预测的基础上利用当前量测来做出修正。根据目标的状态转移服从一阶马尔科夫过程，所以预测和更新过程可以分别描述为:

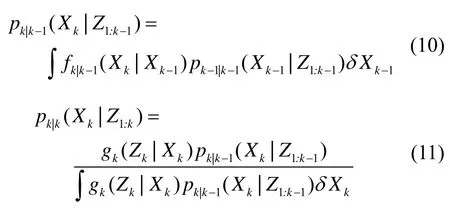
式中:fk|k-1(Xk|Xk-1)是状态转移概率密度;gk(Zk|Xk)为似然函数。最后再利用后验概率密度去估计目标的状态。

2.1 概率假设密度滤波

PHD 滤波是贝叶斯滤波的一种智能近似，通过传递后验概率密度的一阶统计矩来代替后验概率密度函数，可以有效避免数据联合问题。

k时刻的预测密度和后验密度分别用vk|k-1和vk表示，则PHD 滤波的预测可描述为:

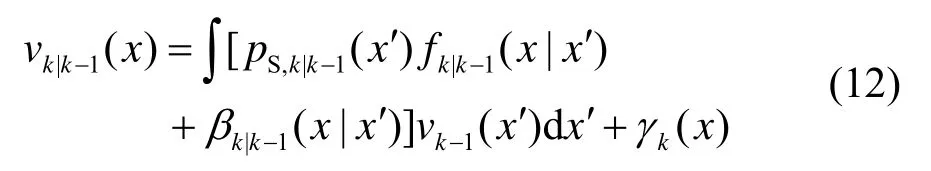
式中:fk|k-1(⋅|x′)为已知目标状态x′转移到k时刻的转移概率密度;pS,k|k-1(x′)为目标x′存活的概率;βk|k-1(⋅|x′)为目标x′在k时刻衍生RFS 的强度;γ(⋅)为新生RFS 的强度。

PHD的更新利用k时刻多目标的量测信息和预测的概率密度，所以后验密度可描述为:

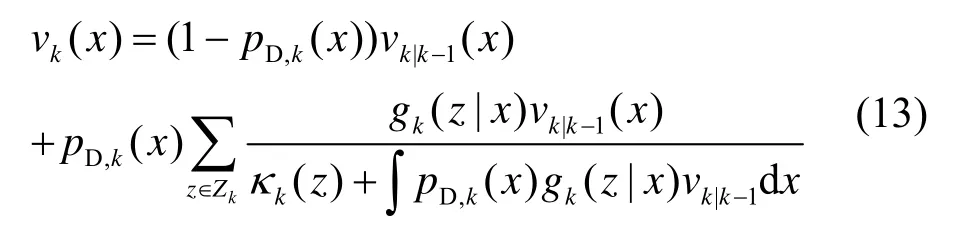
式中:pD,k(x)为k时刻的检测概率;Zk为k时刻多目标的量测;κk(⋅)为杂波RFS 的密度。

2.2 JMS-SMC-PHD 滤波实现TBD

PHD 的序贯蒙特卡罗实现也称PHD 的粒子滤波实现，是用一组带权值的粒子去近似估计目标的后验概率密度。跳跃马尔可夫系统下的 PHDvk-1(xk-1,rk-1|Z1:k-1)用一组带权值ωk-1(s)的粒子表示为:

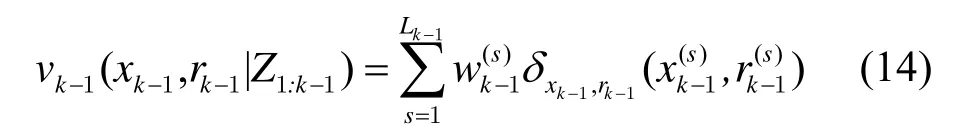
式中:δ(⋅)为狄拉克函数;rk-1为模型标签;Lk-1是存活粒子数。然后通过预测和更新阶段实现滤波:

1)预测:包含了新生粒子的产生和持续存活粒子的传递，新生粒子是由k-1 时刻的量测集zk-1={zk(i,j),i=1,…,n,j=1,…m}通过降序排列后，强度较大的前M个分辨单元所产生的Jk个新生的粒子。由于在强度较大的位置是真实目标所在位置的概率比较大，所以这样产生的粒子更加接近真实目标。假设qk( ⋅|xk-1,Z1:k)和pk(⋅|Z1:k)分别为存活目标和新生目标的重要密度函数。则预测PHD 可近似为:

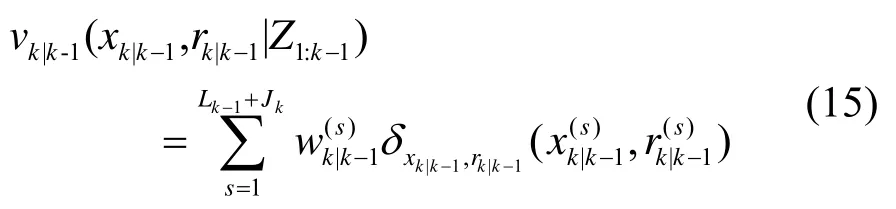
式中:

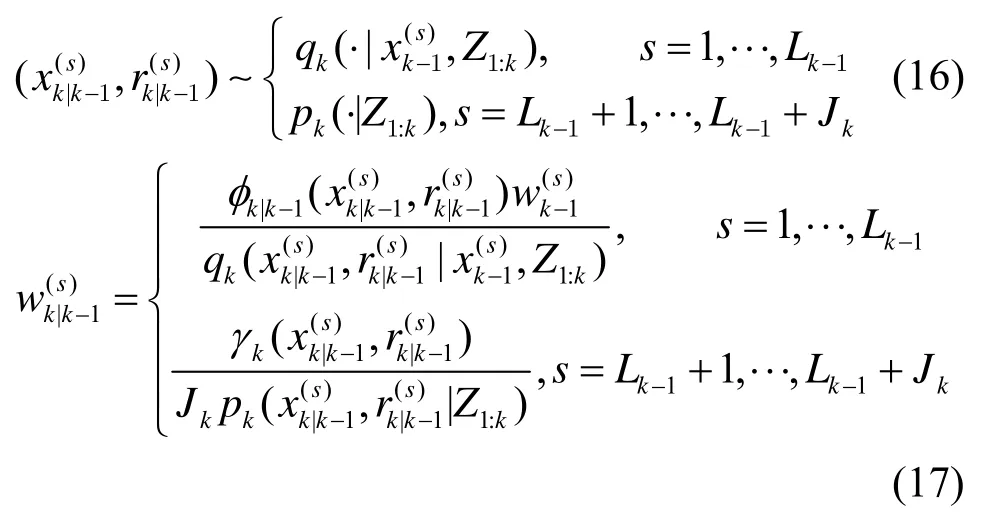
式中:

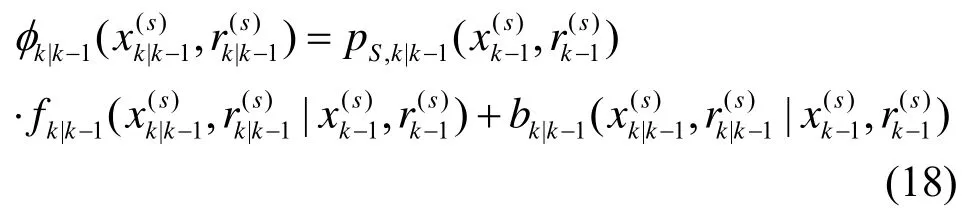
其中，衍生密度函数为:

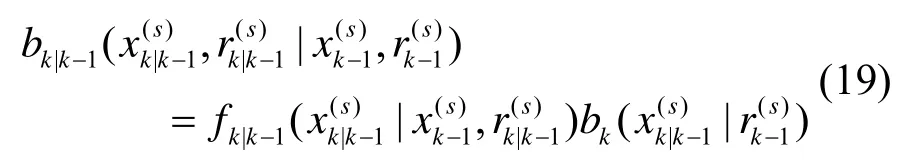
马尔可夫转移概率密度为:

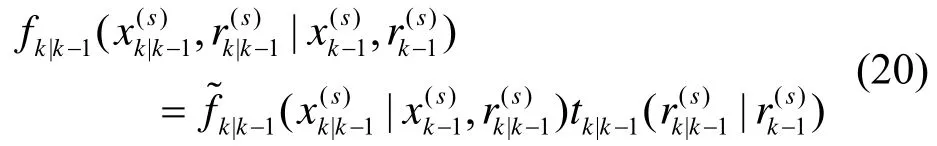
2)对上述得到的粒子根据量测进行粒子权值的更新，对于在量测zk中，仅有那些邻近的分辨单元受到较大影响，因此似然比可计算为:

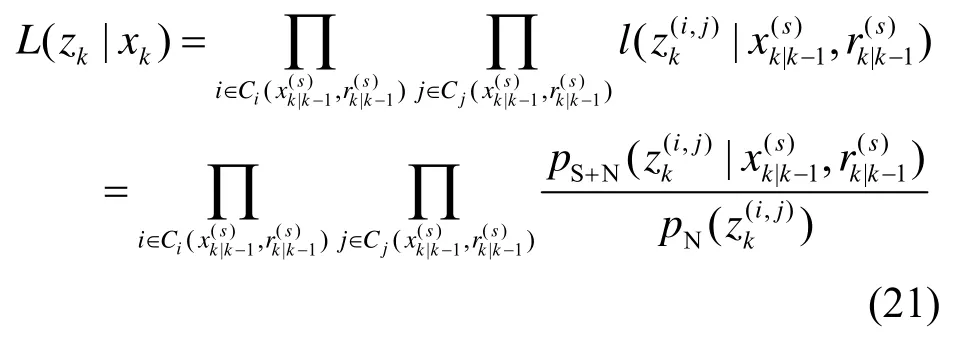
假定由状态xk引起的有效量测为:从而对于状态的权值更新为:

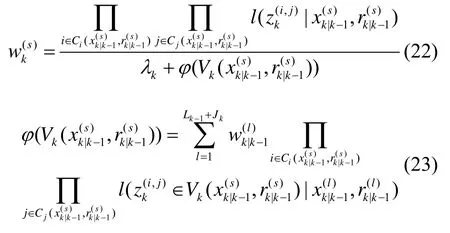
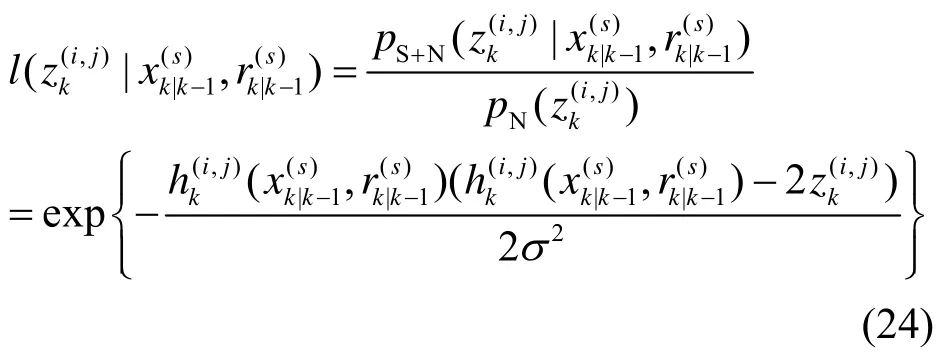
得到了更新权值后，后验密度可表示为:

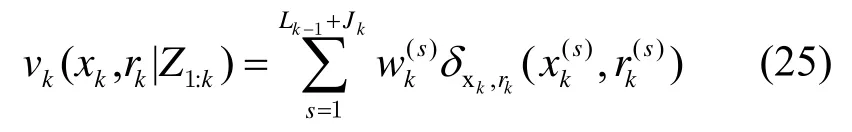
5)提取目标的状态:根据估计目标数zk利用k_means 方法对重采样后的粒子进行聚类划分，从而提取目标的状态。

3 仿真分析

本章给出多机动目标TBD 仿真实验，仿真中目标在3 个模型中相互切换，分别为直线匀速，左转弯运动和右转弯运动。目标的运动模型为:

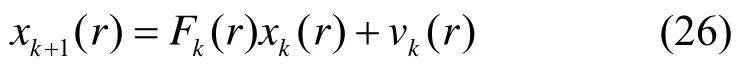
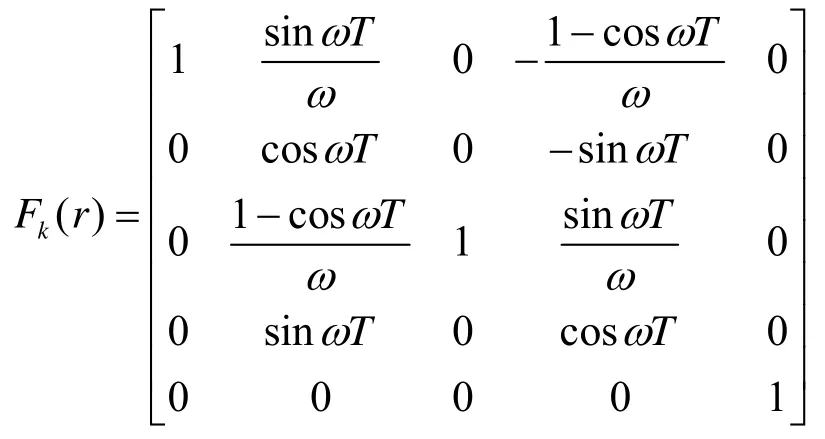
vk为零均值高斯白噪声，其协方差为:

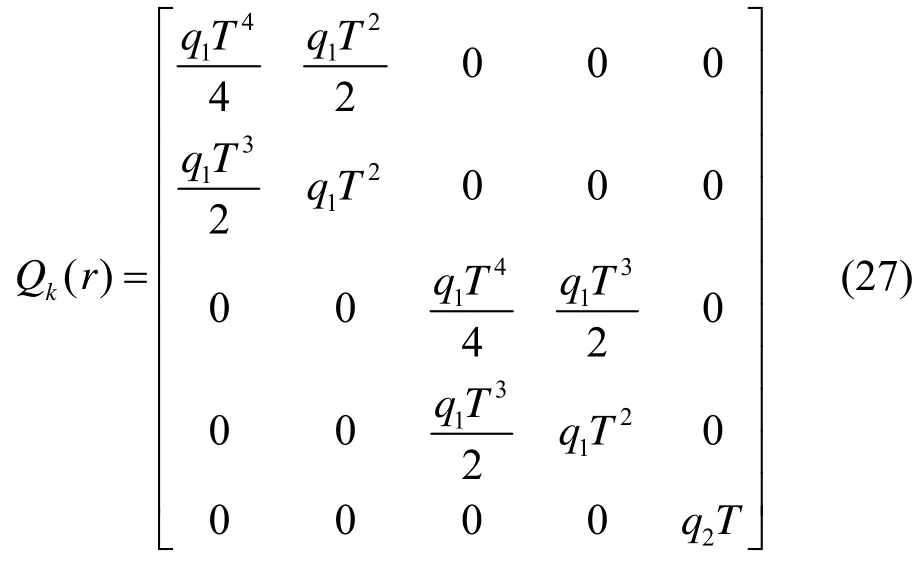
式中:q1=2，q2=1 分别表示目标运动和强度的过程噪声大小。模型r=1 时，为匀速直线运动模型，模型旋转角度ω=0 rad/s;模型r=2 时，模型旋转角度ω=10 rad/s;模型r=3 时，模型旋转角度ω=-10 rad/s。马尔可夫转移概率矩阵和新生RFS 模型概率密度分别为:

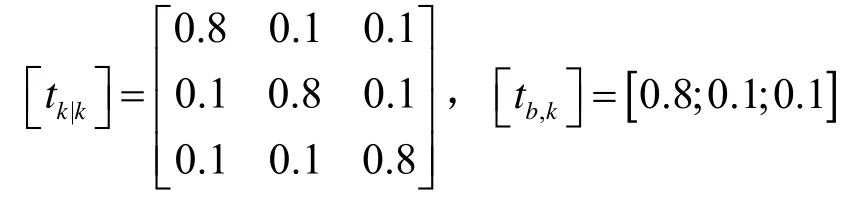
传感器以间隔T=1 s 接收30 帧图像，其他参数值为:Δx=Δy=1，n=m=20，σ=1，∑=0.7。目标的存活概率为Ps=0.98。采用平面中M=20 个最大强度单元作为新生目标的潜在位置，速度均服从U[-0.4,0.4]的均匀分布，强度值服从U[I-1,I+1]的均匀分布，不考虑衍生情况即bk=[0;0;0]。采用最优子模式分配度量(optimal subpattern assignment,OSPA)[17]来检验目标的跟踪精度，OSPA 距是描述集合间的误差的一种有效方法，其最大的优势是同时考虑了两个集合间的势误差(检测精度)和位置误差(跟踪精度)。OSPA 距的参数为:阶数p=1，截断误差c=10。红外传感器强度量测的信噪比为:

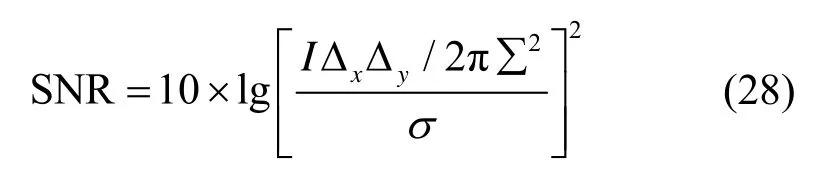
式中:σ为量测图中噪声强度协方差。

将PHD 滤波用于多个弱小目标的检测前跟踪中有一个前提条件，即图像中的每一个单元不能同时被多个目标影响，也就是说多个目标之间不能彼此靠近。假设共有 3 个目标，初始状态为x1=[5,0.3,1,0.4,I]T，从1～25 s 时刻存活。x2=[19,-0.4,9,0.5,I]T，从3～30 s 时刻存活。x3=[5,0.3,18,-0.4,I]T，从6～27 s 时刻存活，其中I=15。图1为真实目标的运行轨迹图。图2为目标位置状态的估计图。由图2可知，估计的目标状态都能近似的分布在真实目标位置附近。

使用Matlab R2013a 运行100 次蒙特卡罗实验。图3为目标状态估计的平均OSPA 误差。本文方法(JMS-PHD-TBD)与目标模型为单一模型的概率假设密度滤波的检测前跟踪方法(SING-PHD-TBD)作比较。由图可知，由于在初始时刻，目标的初始状态选取为空集的情况，所以算法在开始还不能估计出目标的状态，而在目标出现的时候，估计都出现了一定的延时。但JMS-PHD-TBD 的估计误差总体上要优于SING-PHD-TBD。而单模型估计机动目标也能估计出目标的状态是由于新生粒子时采用的是高强度位置产生粒子机制，这样能保证真实目标在所采样的粒子中的概率较高。并且由于弱小目标速度比较小，模型的转换影响会稍微较小，但这也是不容忽视的。

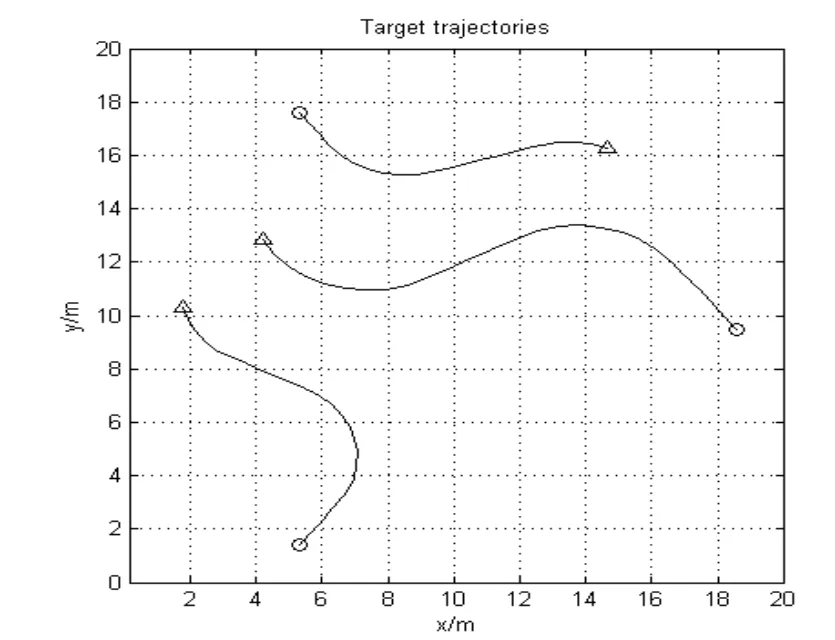
图1 目标真实轨迹Fig.1 Real trajectory of the target

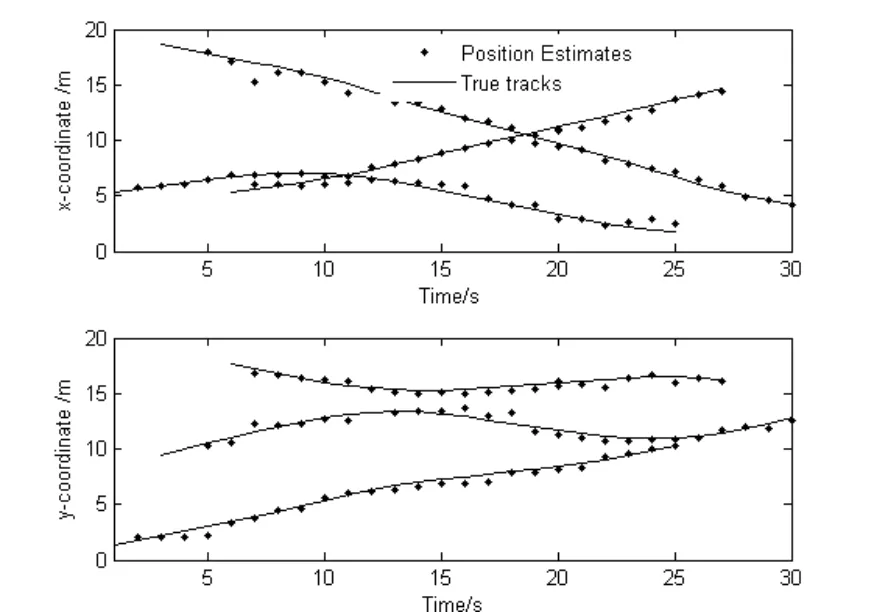
图2 目标位置状态估计Fig.2 Target location status estimation

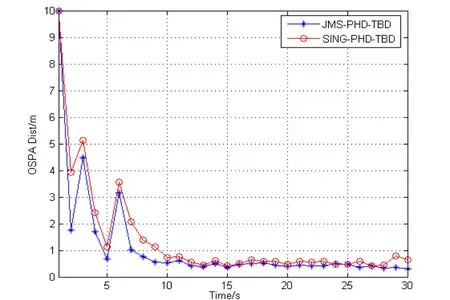
图3 平均OSPA 误差估计Fig.3 Mean OSPA error estimation

图4为100 次蒙特卡罗实验得到的平均目标数目的估计图。由图可知，在新目标出现时，目标数目的估计出现了延时，这也是导致图3中估计的OSPA 误差出现较大峰值的原因。JMS-PHD-TBD 方法对与目标的数目估计更加准确。出现目标跟踪丢失的情况比较少，更加能准确地估计目标的状态。

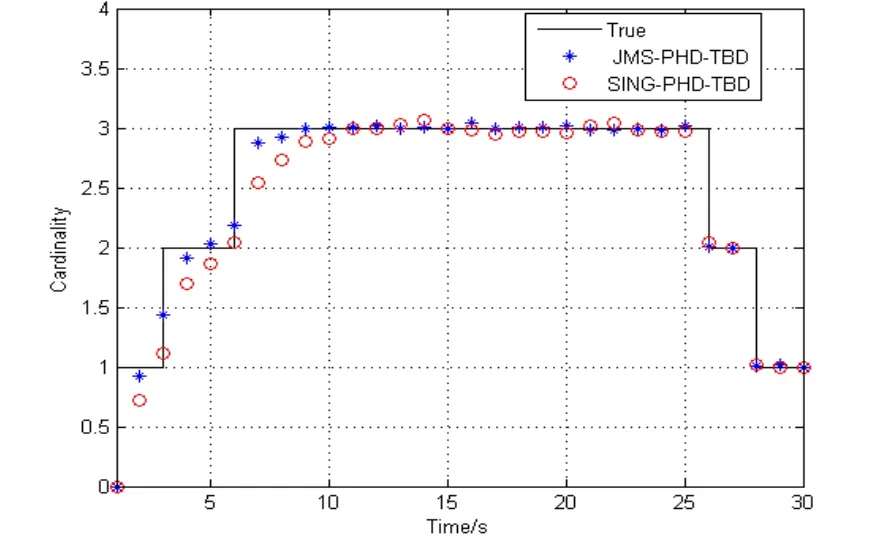
图4 平均目标数目估计Fig.4 Average target cardinality estimation

4 结论

本文对跳跃马尔可夫系统模型下的概率假设密度滤波的检测前跟踪方法进行深入的分析和研究。在序贯蒙特卡罗概率假设密度滤波的基础上，融合跳跃马尔可夫系统，用于解决多机动弱小目标的检测与跟踪。仿真实验表明，通过跳跃马尔可夫系统对模型进行状态转移并直接对单帧量测数据更新权值的处理，可以有效地实现多机动弱小目标的检测与跟踪。