抗饱和内模控制的氩氧精炼铬铁合金碳含量控制系统

2020-09-04姜保良魏丙坤

科学技术与工程 2020年22期

姜保良，魏丙坤，尤文

(长春工业大学电气与电子工程学院,长春 130012)

铬铁合金的冶炼是发生在高温环境下的物理化学反应,通常采用的冶炼方法为向转炉中的初始钢液吹入氧气,促进钢液中的元素与氧气发生反应,达到提纯钢液成分同时控制温度的作用。碳含量的数值是判断合金冶炼是否到达终点的一个极为重要的指标,影响着合金成品的性能。AOD(argon oxygen decarburization furnace)炉冶炼合金转炉冶炼的过程类似,特点在于采用了AOD炉侧顶复吹的方式进行冶炼。对于冶炼终点的控制依然主要采用经验冶炼法,但这一方法往往需要从业人员掌握一定技术来分析炉内钢液的成分与温度掌握[1],要求比较严苛,这使得冶炼终点控制逐渐向自动控制的方向发展。

赵磊等[2]提出了一种通过对炉口火焰进行图象识别,从而对是否到达转炉吹炼终点进行判断和分析的方法。该类方法需要炉口火焰图像质量极高,且图像分析所需时间也会对冶炼终点判断产生影响。现阶段的铁合金企业生产过程中,最常使用的是基于副枪检测,炉气分析或是二者相融合的冶炼终点控制技术[3]。上述方法的缺点在于仍然需要工作人员判断,并决定是否进行干预。因此,越来越多的人将人工智能其运用到冶炼终点控制中,形成新的冶炼终点控制模型。Fei等[4]首次提出将PCA(principal components analysis)和BP(back propagation)神经网络算法融入到转炉炼钢过程中,而Zhou等[5]则融合了深度学习与改进遗传算法,实现了混合模型控制,二者皆基于已有的工程数据进行训练,实现冶炼终点控制,但此方法在实际应用过程中往往需要较大的数据量作为支撑。马海涛[6]在2011 年针对AOD炉建立静态模型,而后在此基础上进行终点控制,提出了一种基于推理控制的AOD炉终点控制方法,其特点在于输出与扰动同时不可测情况下,实现系统稳态无误差。但近些年伴随着LIBS(laser-induced breakdown spectroscopy)技术在世界范围内快速地发展,已然能够实现冶炼过程中碳含量的在线检测[7],满足了输出可测的条件。魏丙坤等[8]基于内模控制(internal model control,IMC)建立了能够保证精度降低冶炼时间的控制系统,但实际冶炼中由于工艺的限制,控制器往往会出现饱和情况。

因此本文设计选择抗饱和内模控制作为整个系统的框架,选择碳含量作为输出,以供氧速率为控制量,建立碳含量与炉内温度二者与供氧速率之间的传递函数,将其前者作为对象模型,后者作为约束条件,且依据实验炉的相关数据,设定了供氧速率饱和约束专家系统,将其作为控制器饱和的约束条件,为使系统在满足不超过温度限制的情况下,实现内模控制器饱和补偿,达到稳态无误差的目标。

1 内模控制及其控制器饱和的影响

内模控制结构框图如图1所示。

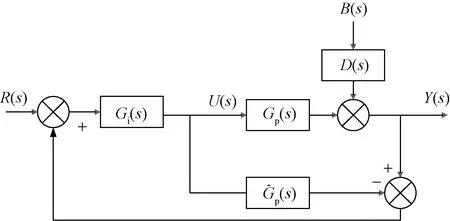
Gi(s)为IMC控制器；Gp(s)为实际机理模型；为控制通道数学模型；B(s)为不可测扰动图1 内模控制结构框图Fig.1 Diagram of internal model control structure

理想条件下,内模控制的控制器应该被设定为

(1)

但上述结构在实际模型中通常是不可实现的,往往需要串联一个滤波器,进而将IMC控制器设计为[9]

(2)

若建立模型与假设对象的传递函数相等,即：

(3)

则可在设计内模控制器时选择串联一阶滤波器,进而将内模控制器设计为

(4)

当给予系统阶跃信号时,可求得控制器的输出量为

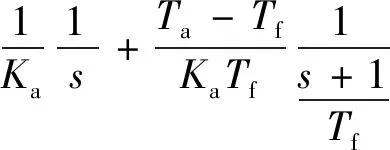
(5)

对式(5)进行反拉普拉斯变换,得到控制器输出量的时域函数为

(6)

若TaTf,则可以求得:

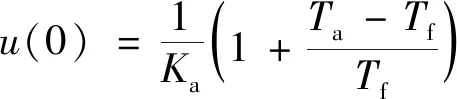
(7)

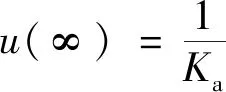
(8)

2 抗饱和设计

为保证控制器稳态无误差,需要对内模控制结构进行必要的改进,从而使得改进后的控制器控制量输出能够跟随内模控制的实际输出,进而达到预期的控制效果,保证系统稳态无误差[10]。改进后的抗饱和IMC结构如图2所示。

图2 抗饱和内模控制结构框图Fig.2 Diagram of anti-windup internal model control

由图2可知,将传统的内模控制器分成了Q1(s)和Q2(s) 两个控制器部分,三者满足条件为

Gi(s)=[Q2(s)+I]-1Q1(s)

(9)

式(9)中：分解出的Q1(s)部分需要通过设计滤波器f(s)获得。Q1(s)的表达式为

(10)

同时,Q2(s)的表达式为

Q2(s)=Q1(s)Gi-1(s)-I

(11)

结合图2,能够求出传统内模控制器输出为

(12)

对式(15)进行变形,可以得到时域表达式为

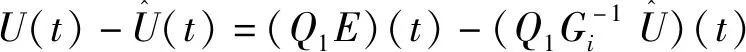
(13)

通过文献[10]可知,若通过设计设计滤波器f(s),使得Q1(s)为一个常数,再对系统进行优化后,可以很大程度地提高系统的性能,使受到控制器饱和约束的内模控制器输出控制性能够得到补偿,接近传统的内模控制器的控制性能。

3 冶炼过程模型

3.1 机理模型的基本假设

针对AOD炉侧顶复吹冶炼铬铁合金的过程作如下假设。

(1)将初始铬铁熔液视为高铬铁基熔体,无论熔液内其他元素的质量分数如何,吹入炉内的氧气均首先与Fe元素生成FeO,而后该物质则作为炉内二次反应的氧化剂。

(2)高温冶炼阶段的钢液与废渣熔液均为理想溶液,其中各组分活度为其摩尔分数。

(3)钢液与熔渣的初始质量,及其初始成分C,Si、Cr以及Fe等元素的数值,废气温度,吹入气体的初始温度,均为已知。

(4)整个冶炼过程中,钢液中各元素的氧化速率均与供氧速率有关,且将铁水中各组分元素氧化反应的吉布斯自由能之比作为该元素氧化反应时所分得的氧气比例[11]。

(5)铬铁合金熔液中只考虑C、Si、Cr、Fe四种元素,其余元素的氧化暂不考虑。

3.2 机理模型的参数确定

对于氩氧精炼过程,供氧速率是反映炉内各元素参与反应过程的最主要反应参数。由文献[8]可知,在供入氩气进行精炼过程中，脱碳速率公式为

(14)

AOD炉温度平衡公式:

WmcmT+QOdtρOcOT0+QsubdtρsubcsubT0+WscsT+

QsubdtρsubcsubTd

(15)

式(15)中：ai为i元素的活度系数；Xi,O为组分元素i的分氧比；Wm为钢液总质量；Ws为熔渣总质量；cs为熔渣比热容；η为氧气利用率；QO为供氧速率；Qsub为惰性气体供给速率；ΔHi为组分元素i的熔化焓；T为钢液温度；T0、Td为气体温度及其初始温度；ρi为i物质的密度；ci为i物质的比热容；Mi为i物质摩尔质量；w( )为物质在熔液中所占百分比；

3.3 冶炼机理模型建立

将各项参数代入到式 (14) 中,进行求解,通过计算,求出碳含量变化速率与氧气供给速率的关系式:

(16)

对式(16)求拉普拉斯变换,得到钢液中碳含量与供氧速率之间的传递函数为

(17)

同样的,将参数代入可得温度变化率与供氧速率的关系式:

2.23×10-5T

(18)

对式(18)化简并求拉普拉斯变换,建立AOD炉内钢液热平衡方程。同时,针对AOD炉的热损失,结合实验炉的相关数据,做了一维稳态传热过程的假设[12-13],将炉体看作单层圆筒壁,将炉体分为上下两个部分进行模型建立。上半部分为炉内气体通过四面炉壁向外散热的过程；下半部分则是炉内铁水通过炉壁与炉底向外传热的过程。并将二者相加,视作整个炉体的热损失。

进而求解得到炉内温度与供氧速率之间的传递函数:

(19)

4 仿真分析及实验对比

4.1 仿真结果

本次建立的系统以碳含量为输出,供氧速率为控制量,在实际进行氩氧精炼低碳铬铁合金的过程中,初始铬铁熔液中碳含量为8%,最终要求的碳含量为0.25%。实验用炉为单一顶枪,双侧枪的设置,顶枪与一侧枪吹入氧气,另一侧枪则向炉内吹入氩气,顶枪的最大供氧速率为1 000 Nm3/h,侧枪的最大供氧速率100 Nm3/h。当碳含量高于1%时,冶炼过程采用侧顶复吹的方式,最大供氧速率为1 300 Nm3/h,即361 000 cm3/s,当碳含量介于1%～0.25%时,采用纯侧吹的方式,最大供氧速率为300 Nm3/h,即83 000 cm3/s。因此针对上述两段最大供氧速率的限制,建立供氧速率饱和约束专家系统,分别进行两个阶段控制器的限制。具体参数如表1所示。

表1 供氧速率饱和约束专家系统

针对滤波器时间常数为300的内模控制器进行抗饱和设计,所求的控制器与饱和补偿器的传递函数分别为

(20)

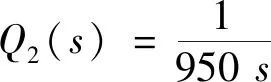
(21)

在实际冶炼过程中,为确保成品铬含量达标,会在出炉前投入含碳铬铁,在仿真过程中设为4 500 s时,存在0.5倍阶跃的外界扰动信号。

图3为滤波器时间常数为300的理想内模控制控制量曲线与有饱和约束但未进行饱和补偿的内模控制控制量曲线,除饱和部分外,其余部分二者曲线重合。图4为滤波器时间常数为300的理想内模控制输出曲线与有饱和约束但未进行饱和补偿的内模控制输出量曲线,在有效时间内,前者有着更好地动态响应性能,更快地到达稳态终点。

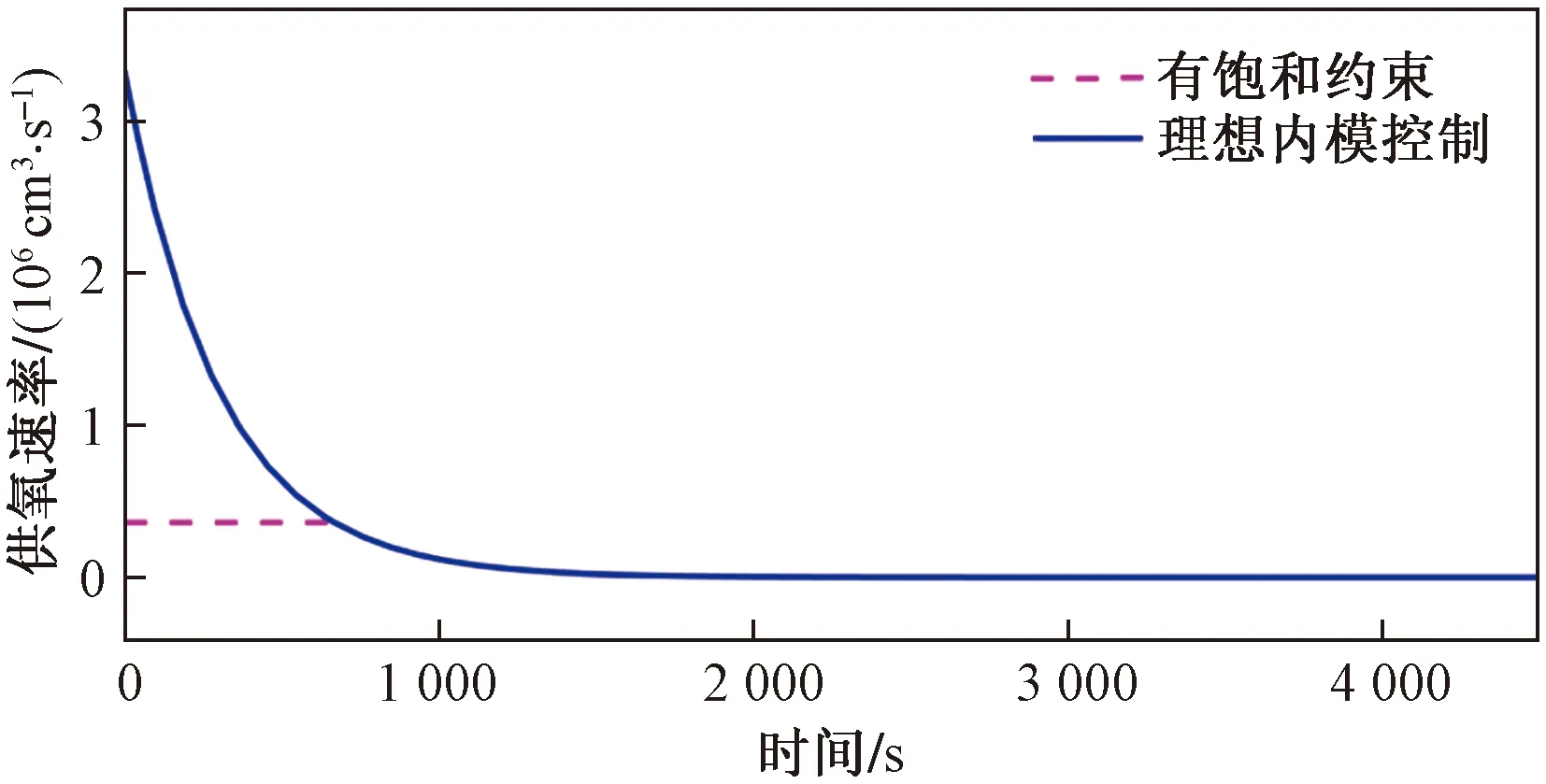
图3 理想内模控制控制量与有饱和约束控制量Fig.3 Ideal internal model control and control with saturated constraints

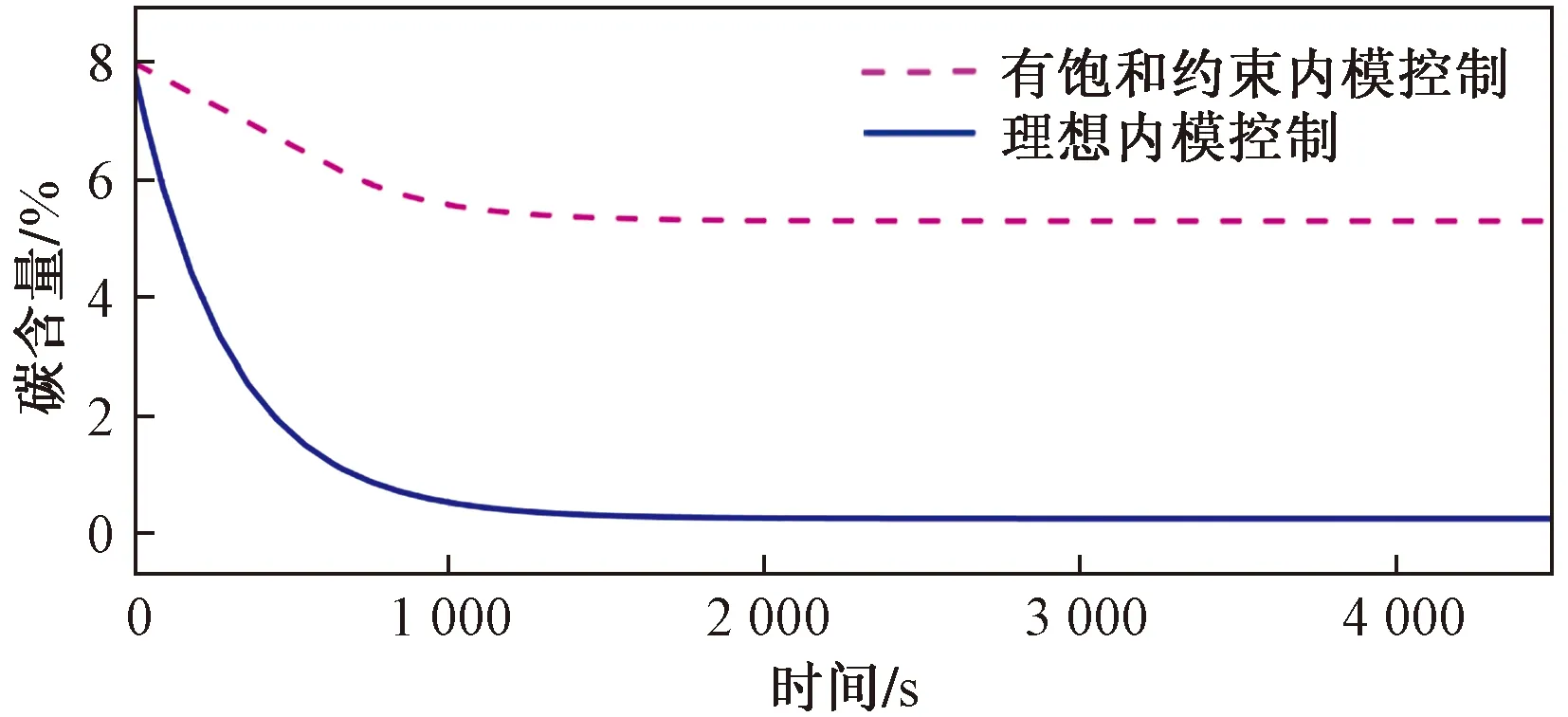
图4 理想内模控制输出与有饱和约束内模控制输出Fig.4 Ideal internal model control output and internal model control output with windup constraints

图5为滤波器时间常数为300的理想内模控制控制量曲线与在其基础上,进行饱和补偿的抗饱和内模控制控制量曲线,从图5中可以看出,后者对饱和部分所缺失的控制量进行了必要的补偿。图6为滤波器时间常数为300的理想内模控制输出曲线与在其基础上,进行了饱和补偿的抗饱和内模控制的输出曲线,二者均能达到最初设定的稳态,精度得到有效保障,但是加入抗饱和的内模控制比理想内模控制需要更长的时间达到预设目标。

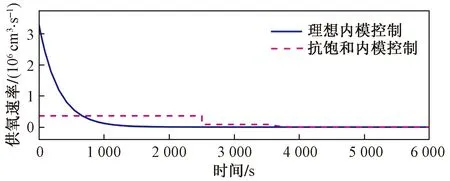
图5 理想内模控制控制量与抗饱和内模控制控制量Fig.5 Ideal internal model control and anti-windup internal model control

图7为以滤波器时间常数为300的理想内模控制为基础,进行饱和补偿的抗饱和内模控制控制量曲线与符合两个阶段供氧速率要求的理想内模控制控制量曲线。图8以滤波器时间常数为300的理想内模控制为基础,进行饱和补偿的抗饱和内模控制输出曲线与符合两个阶段供氧速率要求的理想内模控制输出曲线,结合两图可见,前者比后者更快地实现初始设定的冶炼目标,大幅度地缩短了冶炼时长。

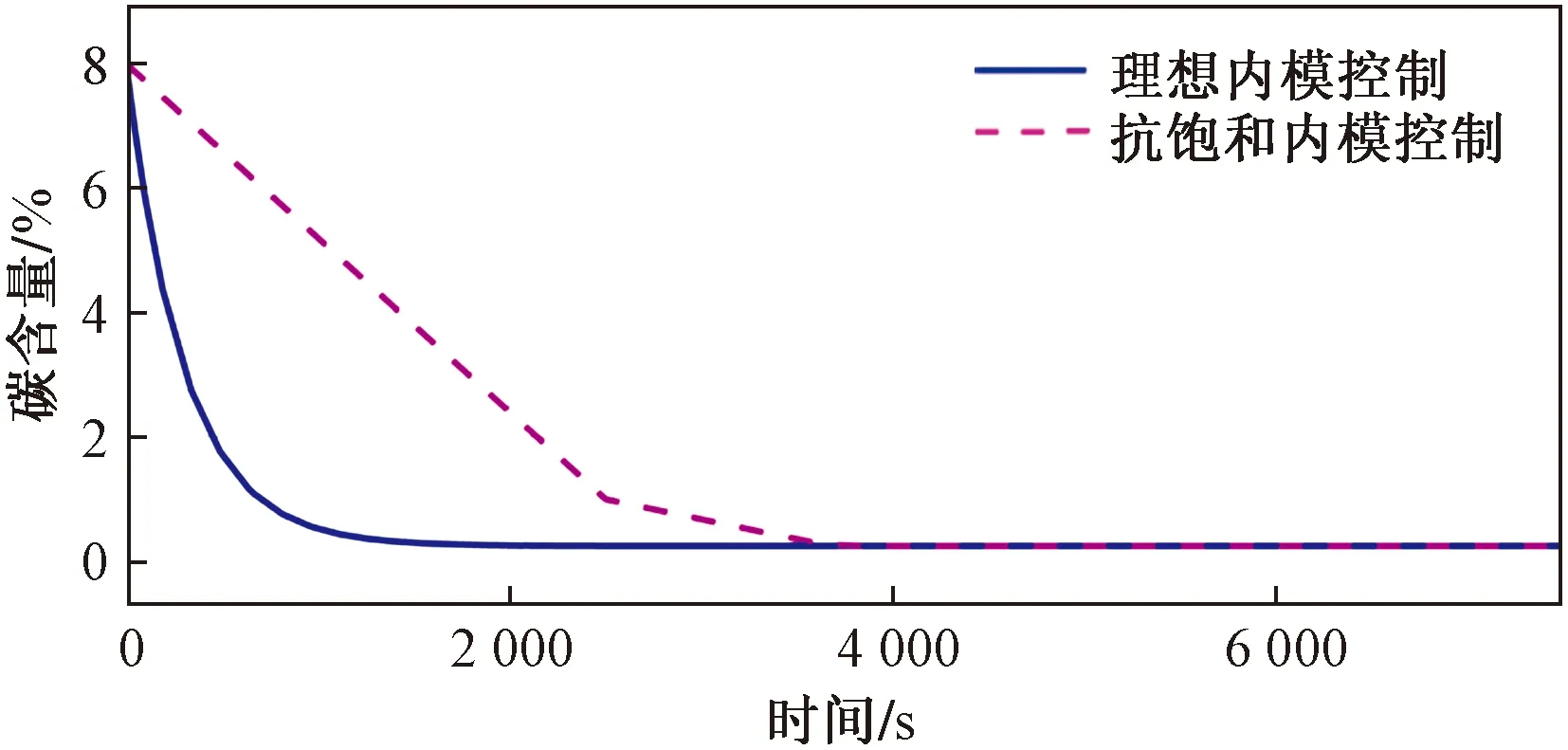
图6 理想内模控制输出量与抗饱和内模控制输出量Fig.6 Ideal internal model control output and anti-windup internal model control output

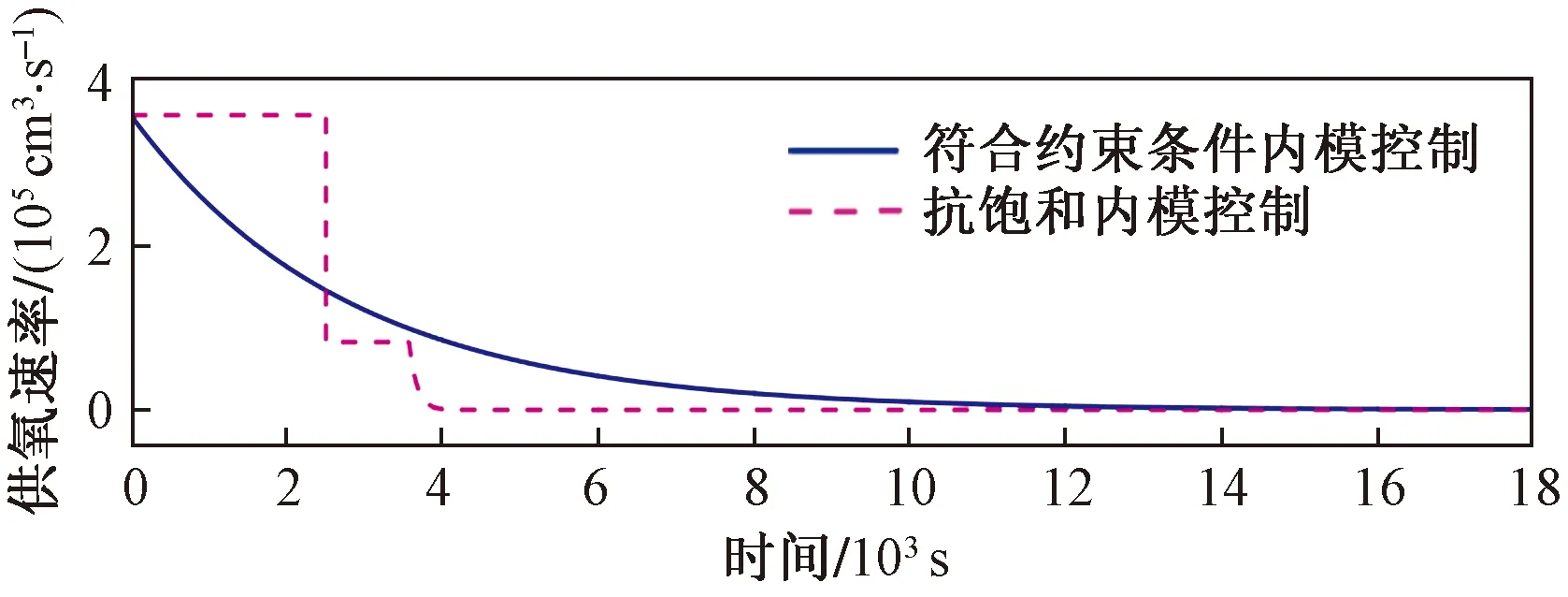
图7 符合约束条件内模控制控制量与抗饱和内模控制控制Fig.7 Control parameters of internal model control and anti-windup internal model control

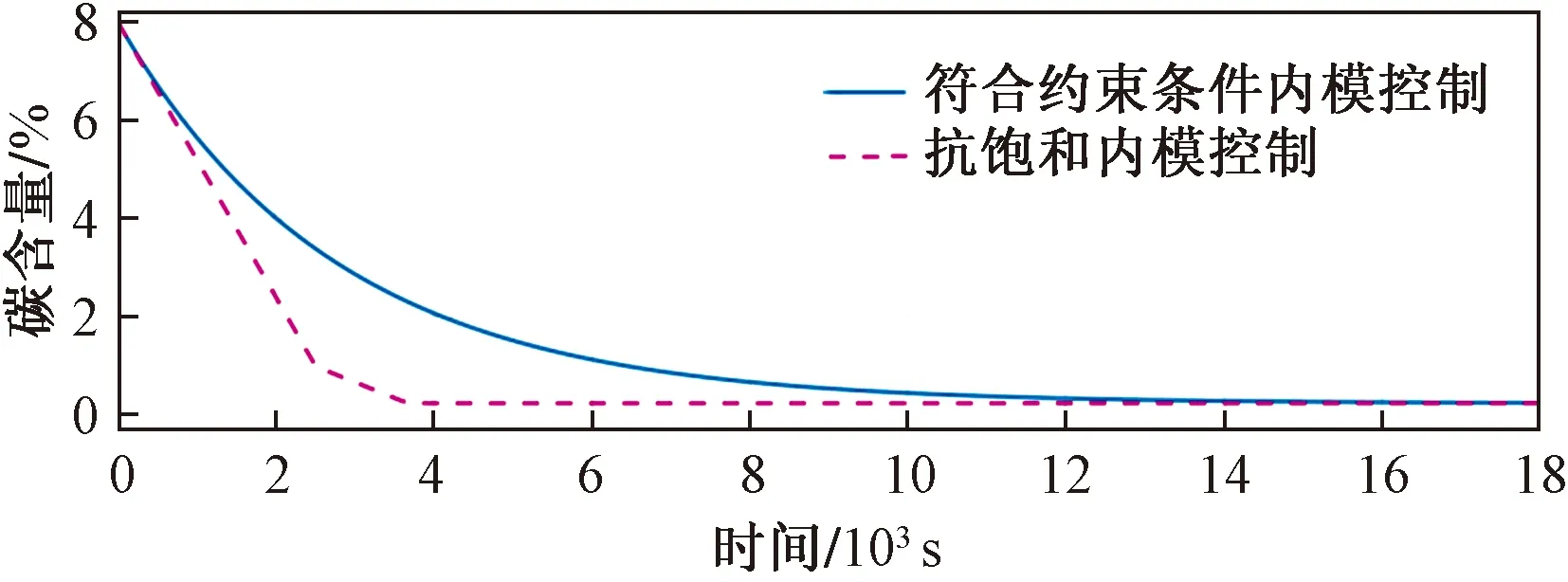
图8 符合约束条件内模控制输出量与抗饱和内模控制输出Fig.8 Meet the constraints of the internal model control output and anti-windup internal model control output

图9比较了所设计抗饱和内模控制系统中所建立模型与实际被控对象存在正或负误差时的实际输出曲线。分别假设实际对象模型传递函数为-5.5×10-9/s与-8.5×10-9/s, 从图9中能够看出,无论是与模型存在正误差,或是存在负误差,本次设计的系统均能够实现预期的冶炼目标,稳态误差为零,差距在于冶炼的总时长。

图9 模型与对象存在正负误差输出Fig.9 Model and object had a error of plus or minus output

图10比较了所设计抗饱和内模控制系统中所建立模型与实际被控对象存在阶次误差时的实际输出曲线,建立的传递函数为一阶传递函数,现假设对象传递函数为二阶传递函数,取为-7.74×10-9(s+1)/(s2+s)。从图10中能够看出,即使所建模型与实际被控对象的传递函数存在阶次误差,本系统也能够达到预期的冶炼目标,实现稳态无误差。