地铁轨道不平顺状态的监测与预警

常 惠，饶志强，赵玉林

(1.北京联合大学北京市信息服务工程重点实验室,北京 100101；2.北京联合大学城市轨道交通与物流学院,北京 100101)

在中国轨道交通快速发展的同时,列车数量和行车密度也在不断增加,轨道交通设备质量和性能的重要性也越来越突出,轨道不平顺严重威胁列车安全和设施设备的使用寿命等[1]。在地铁的长期运行中,轨道线路的一些安全问题或隐患很难立即被发现。所以对地铁轨道设备进行实时地监控就显得尤为重要,特别是对影响铁路运输能力和行车安全的轨道质量的监测具有重要的意义[2]。基于光学原理的光纤光栅传感技术近年来发展迅速,在铁路轨道状态监测方面也得到了应用,张政[3]利用光纤光栅传感技术对高速铁路的轨道使用状态进行监测；周雪芳[4]利用光纤光栅感测系统记录轨道模型,作为轨道变形和安全监测的有效方式；陈志颖[5]使用光纤光栅压力传感器来检测列车是否占据轨道部分的设施设备,并评估轨道电路分支状态列车的安全性。在轨道质量预测方面,由于中国主要采用轨道质量指数(track quality index,TQI)来评判轨道状态,针对TQI预测,常用的方法有综合因子法[6]、神经网络预测方法[7]以及灰色组合预测方法等[8-11]。在轨道不平顺各单项标准差的研究上,左玉云等[12]分析了郑武线上轨道高低、轨向以及水平不平顺之间的线性关系；练松良等[13]分析了车体加速与轨道高低、轨向、水平平顺之间的关系；房建等[14]分析了车体震动加速的相关问题；李仕毅等[15]利用灰色成分数据模型对轨道不平顺指标进行建模分析。当前在TQI综合指标方面的研究较多,但对单项指标的研究仍不够全面,没有对各个方面整体变化规律的建模分析,导致TQI的波动较小，无法反映轨道的实际运行状态。

基于上述问题,本文以轨道不平顺的各单项标准差作为研究对象,利用光纤光栅传感器对其进行监测,根据实际监测数据进行TQI权重统计和超限率分析,结合轨道状态数据的特征,构建GM-PSO-Elman组合预测模型,模型具有收敛速度快,保证获得全局最优解的优点。根据实际数据进行建模分析,对模型的有效性、可行性及优越性进行实例验证,实现轨道不平顺各单项指标几何状态的超限预警,能够有针对性地高效率、高质量、低成本地消除线路病害,提升轨道线路的质量,为城市轨道交通的安全运营提供保证。

1 轨道状态数据分析

1.1 轨道状态数据采集

利用传感器对轨道状态进行实时地跟踪监测,即在线路上放置大量固定监测点进行长期监测和检测,并将采集的数据进行分析,而光纤光栅传感器的灵敏度和精度都很高,具有较强的抗电磁干扰能力,并且体积狭小便于灵活安装在地铁轨道结构狭小的工作环境下,能够满足轨道结构中很多毫米级参量值的监测精度和要求,光纤传输效率高且传输距离长,是监测带状轨道结构的理想选择。

选用光纤光栅传感器对轨道不平顺的七项参数进行监测,在轨道上安装传感器和保护工具,将光缆的走线进行连接并在表面进行钻孔固定。利用无线网络远程传输监测数据,位于现场的光纤光栅解调器和无线模块频繁进行数据采集,并将数据进行存储和网络传输,以提供跟踪状态监测和预警。通过对比在北京地铁9号线现场实验监测采集到的轨道不平顺各单项标准差与轨检车检测的数据,包括左右轨向、左右高低、水平、轨距、三角坑七项参数,结果显示二者具有很好的一致性,表明通过光纤光栅传感器实时监测钢轨质量是可行的,可作为轨道变形和安全监测的有效方法。数据的监测时间为2017年1月—2019年2月,期间每月中旬检测一次,共25组数据。监测数据如表1所示,单位为mm。

由表1可以看出,轨道各单项数据离散性较大,轨道不平顺状态的变化不具明显的规律,这也是北京地铁客流量多和人群密度大的原因造成的,该监测区段又属于道岔、曲线地段,是地铁安全运营养护作业的重点和难点,因此作为实验验证的典型区段进行分析。

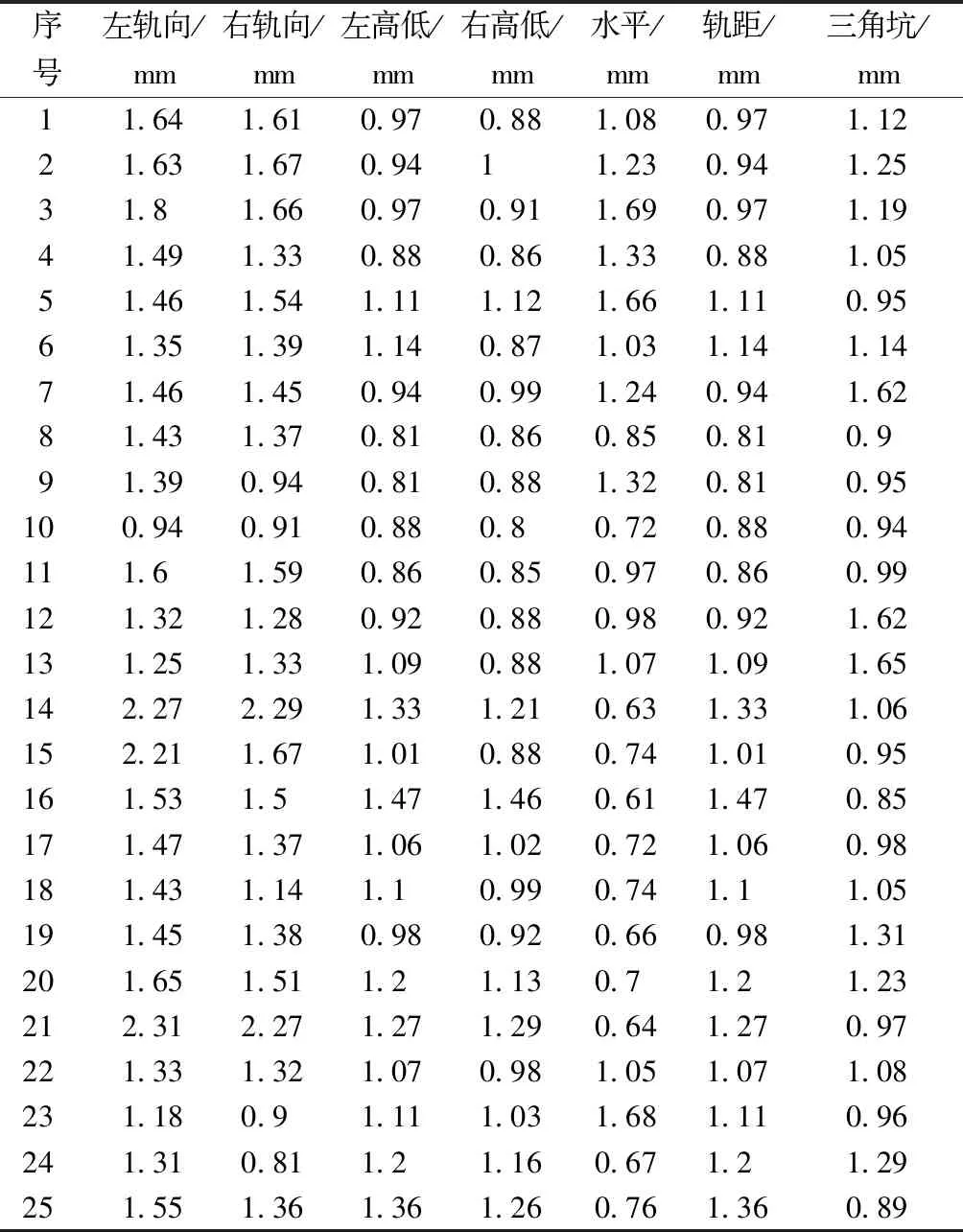
表1 原始轨道不平顺状态监测数据

1.2 TQI权重统计

轨道质量指数(TQI)是左右轨向、左右高低、水平、轨距和三角坑等七项不平顺指标在200 m区段上的标准差之和,它用来反映轨道的平顺度。利用光纤光栅传感器实际监测七项数据求和即可得到TQI数值,通过对轨道单元区段单项指标进行权重统计可以确定需要重点维修的地方,更符合轨道线路实际运行的质量情况。对9号线实际监测的七项指标在TQI中所占的权重进行统计,如图1所示。

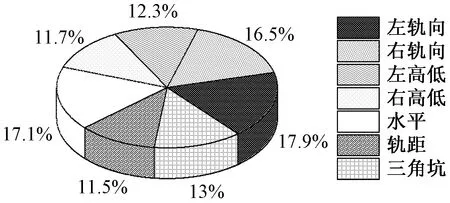
图1 七项指标权重统计图Fig.1 Weighted chart of seven indicators

由图1可见,9号线左轨向占的权重为17.9%,水平占的权重为17.1%,右轨向占的权重为16.5%,相对其他单项来说在TQI中所占的比例较大,在日常维护和大修中要特别注意这三个方面。当发现轨道质量出现问题的时候,要着重查看这几项指标的情况,更有针对性地对轨道线路进行养护维修作业,切实提高天窗修的质量和维护工作的效率。

1.3 超限统计

根据轨道不平顺管理值判断其是否超限及超限详情,将超限部分的数据与单元轨道区段的各项标准差进行比较,对单元区段的超限情况进行统计并计算加权平均值,查看超限较为严重的指标来指导轨道寿命分析及养护工作。根据北京市地方标准《城市轨道交通设施养护维修技术规范》中轨道动态不平顺均值管理的规定,轨道质量指数管理值如表2所示,对北京地铁9号线两年的TQI超限情况进行统计,根据管理标准值绘制出超限分数分项比例图,结果如图2所示。

表2 轨道质量指数管理

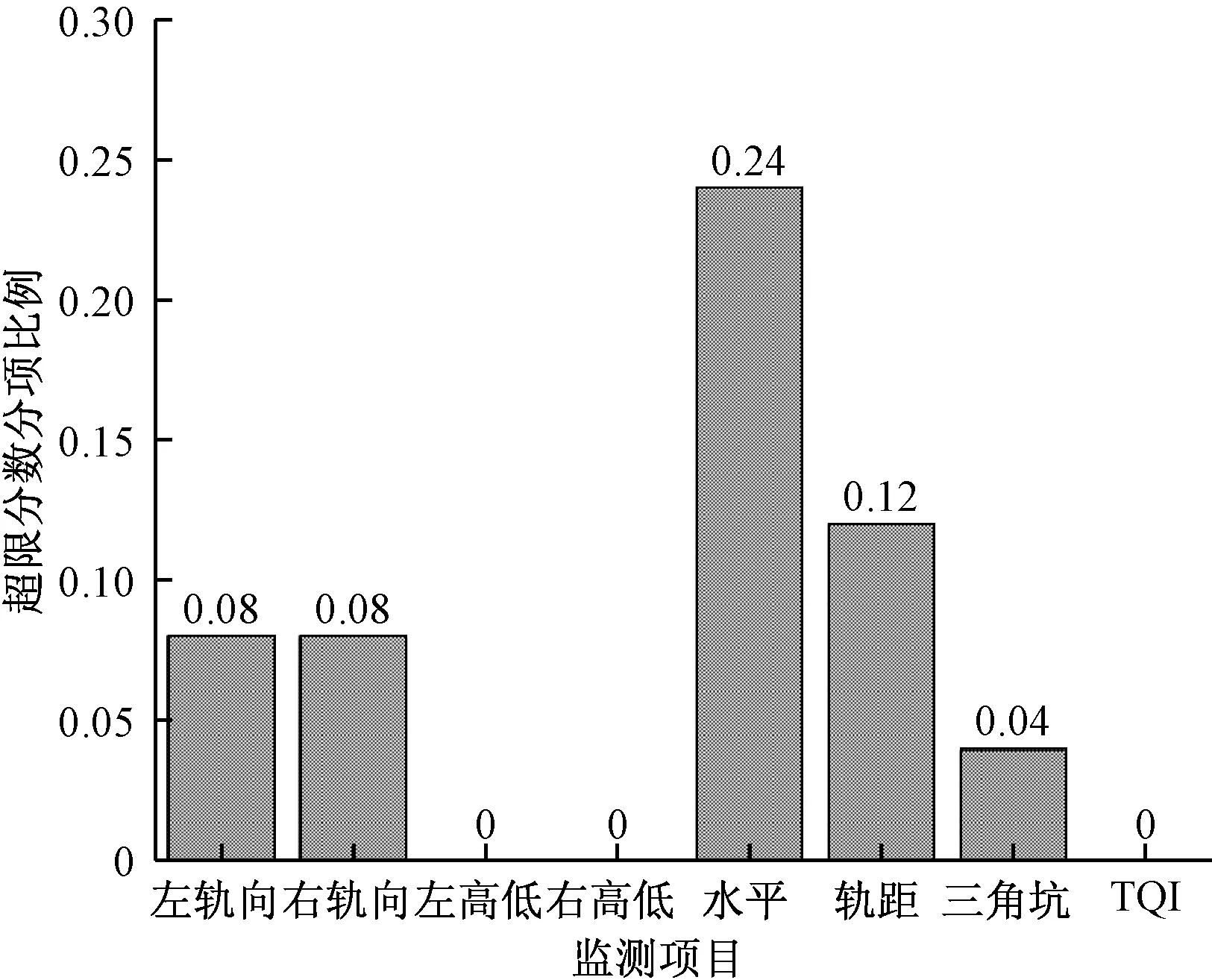
图2 超限分数分项比例Fig.2 Sub-item ratio of over-limit score

由于TQI为轨道综合的评价指标,仅限于设置单位区段的长度,当有单项指标发生严重不平顺,而其他指标正常时,TQI的变化并不明显,无法将轨道的真实病害情况反映出来。从图2中可以发现,在这两年的时间内水平的超限情况较严重,超限率达到了24%,但TQI无超限情况,说明线路状态优秀。当TQI超限时,说明线路质量很差,需要进行紧急维修。根据实际分析结果加大对超限率较高的指标进行维护检查,编排相应的轨道养护维修计划,真正实现以数据为依据的“状态修”科学维修制式。

2 轨道不平顺状态的预测预警

2.1 轨道不平顺特征及预测思路

根据上述数据的分析,可以看出轨道不平顺的动态监测数据几乎没有明显的规律,具有周期性、多阶段性和指数性等特征,而这些特点与灰色系统的特点非常吻合,故可以应用灰色预测的理论和方法来研究轨道不平顺的各单项指标数据；神经网络的预测方法要考虑到各种影响因素,有些信息量化困难,难以确定模型参数。为克服单一模型的缺陷,排除不确定因素的影响,将灰色模型与神经网络结合进行动态预测,分别对轨道不平顺的左右轨向、左右高低、水平、轨距、三角坑七项参数进行验证分析,以探求轨道不平顺内部隐藏的规律并预测未来的数值,从而对线路不平顺状态进行超限预警。

2.2 灰色组合预测模型的构建

灰色GM(1,1)模型适合对小样本的数据进行建模分析建立灰色微分方程,对原始的数据序列进行累加,得到具有指数规律变化的累加序列,将原始数据序列中的随机成分进行弱化,发现隐藏在系统中的有序分布规律,预测结果为有趋势性的平滑曲线。对于轨道几何参数中随机波动性较大的数据序列拟合效果较差、预测精度较低,具有一定的局限性[16]。Elman神经网络[17-18]是一种动态前馈式局部递归神经网络,对灰色模型进行残差校正,可以提高预测精度,其结构如图3所示。

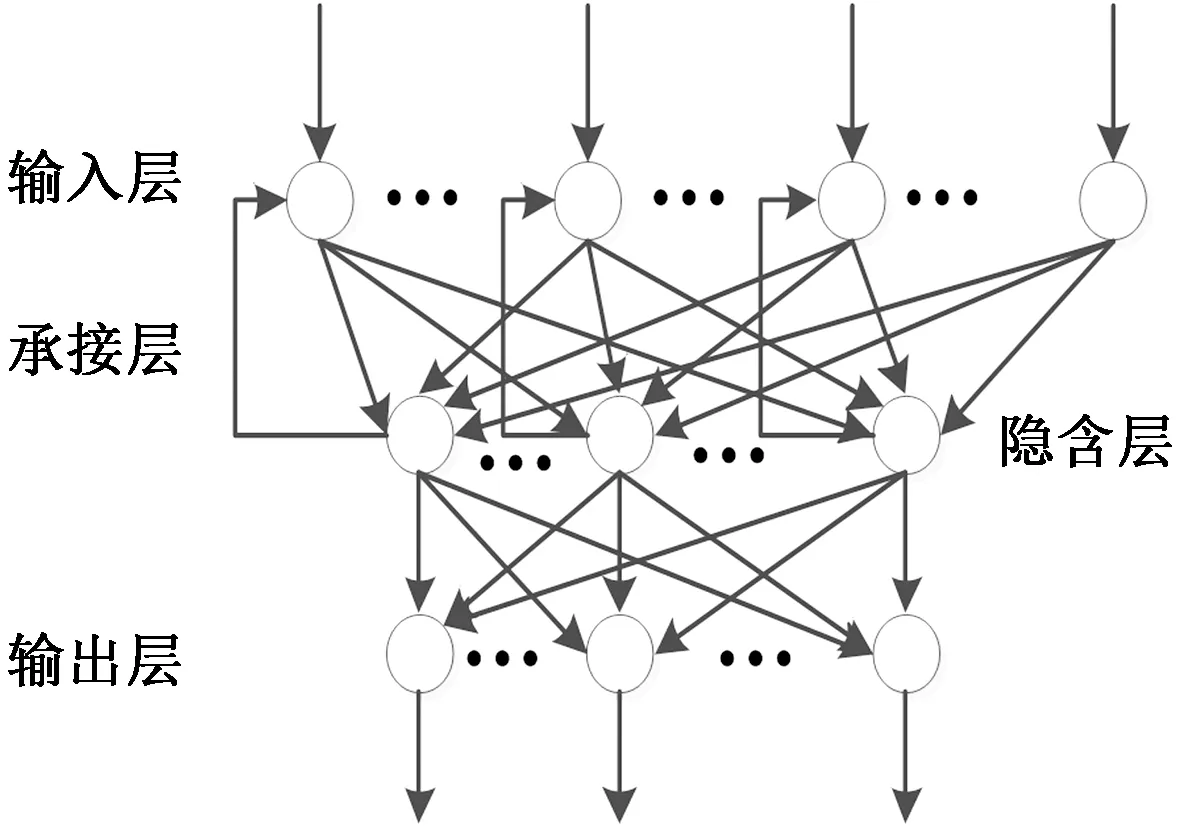
图3 Elman神经网络结构Fig.3 Elman neural network structure

为进一步提高残差校正模型的预测精度,利用粒子群优化算法(particle swarm optimization,PSO)通过其快速的搜索速度和低复杂度的结构以避免陷入局部最优来优化Elman网络的权值和阈值,构建一种以灰色为基础的PSO优化的Elman神经网络组合预测模型,其预测原理:利用灰色模型GM(1,1)预测原始数据序列,初步预测序列与真实的原始序列比较得到残差序列,将残差序列输入到PSO-Elman残差校正模型中,得到校正值,最后输出单项指标的预测值和相应误差值。记原始轨道几何参数X(0)为非负序列：

X(0)={x(0)(1),x(0)(2),…,x(0)(n)}

(1)

(1)原始数据序列进行级数比检验,级数比：

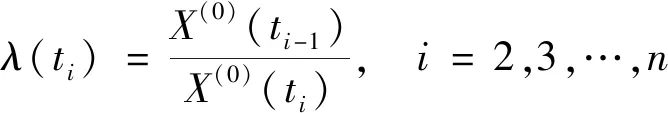
(2)

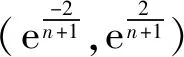
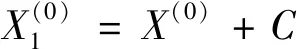
(3)

(2)将级数比检验过之后的数据进行一阶累加生成处理,得到一阶累加序列X(1)：

X(1)={x(1)(1),x(1)(2),…,x(1)(n)}

(4)

(3)将X(1)输入至GM(1,1)模型,利用最小二乘预估得到辨识参数。

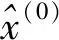
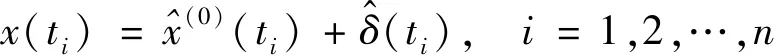
(5)

组合预测模型流程图如图4所示。

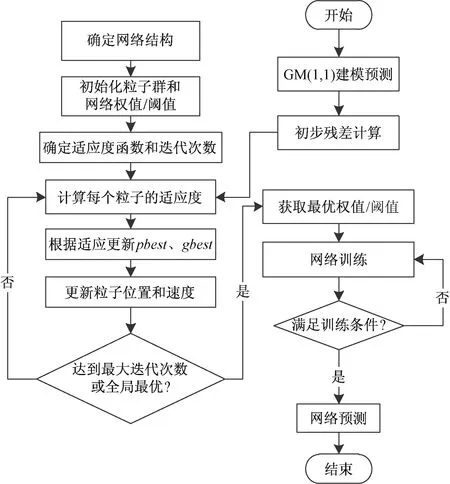
图4 GM-PSO-Elman预测模型流程图Fig.4 Flow chart of GM-PSO-Elman prediction model

2.3 不平顺状态预测实例验证

为证明本文模型的可行性和有效性,实验中同时采用GM(1,1)模型和GM-PSO-Elman模型进行分析比较。每个模型使用相同的训练样本和测试数据集作为控制变量,并且尽可能地设置相同的参数。利用上述北京地铁典型区段监测的数据进行建模,包括左右轨向、左右高低、水平、轨距、三角坑的单项标准差,选取20组数据进行模型训练,剩下5组数据用于预测。

2.3.1 各单项标准差预测结果分析

依据实测数据及函数类型,确定各单项预测模型的基本参数,得到灰色模型初步预测结果,确定残差校正模型参数,其中采用的Elman神经网络结构为5-5-1,即输入层5个节点,隐含层5个节点,输出层1个节点,学习率为0.1,终止条件1.0×10-5。采用自适应变异算子优化网络,种群规模为30,进化迭代次数为100,学习因子c1=c2=1.494 45,最大速度Vmax=1,最小速度Vmin=-1。各单项标准差的预测结果对比如图5所示。

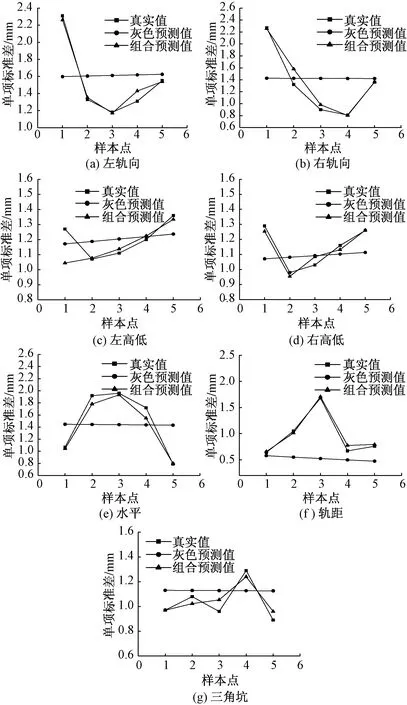
图5 各单项标准差的预测结果对比Fig.5 Comparison of prediction results of individual standard deviations

从图5实验结果看出,灰色组合模型比单一灰色模型对轨道几何状态各单项标准差的预测效果好,灰色模型GM(1,1)可以得到原始几何参数的总体发展趋势,利用粒子群优化的Elman神经网络可以训练找出轨道不平顺状态发展中各因素之间复杂的函数关系,对初步预测序列进行残差校正,将轨道不平顺状态发展趋势中的随机波动成分进行处理分析,充分挖掘原始序列的发展规律,能解决轨道几何状态监测数据序列中的不稳定性和残差较大的非线性问题,进一步提高了预测精度。

2.3.2 不同模型计算结果精度对比

为进一步了解各模型性能和预测精度,更好地确定函数的性能是对各项标准差预警效果的直观表示,也是评价网络设计好坏的标准,一般选择计算误差来充当性能函数的功能。采用如下模型评价指标:平均相对误差(mean relative error,MRE)、均方根误差(root mean square error,RMSE)、决定系数以及相关系数对各单项轨道几何参数的灰色模型和灰色组合预测模型进行对比分析，结果如表3所示。

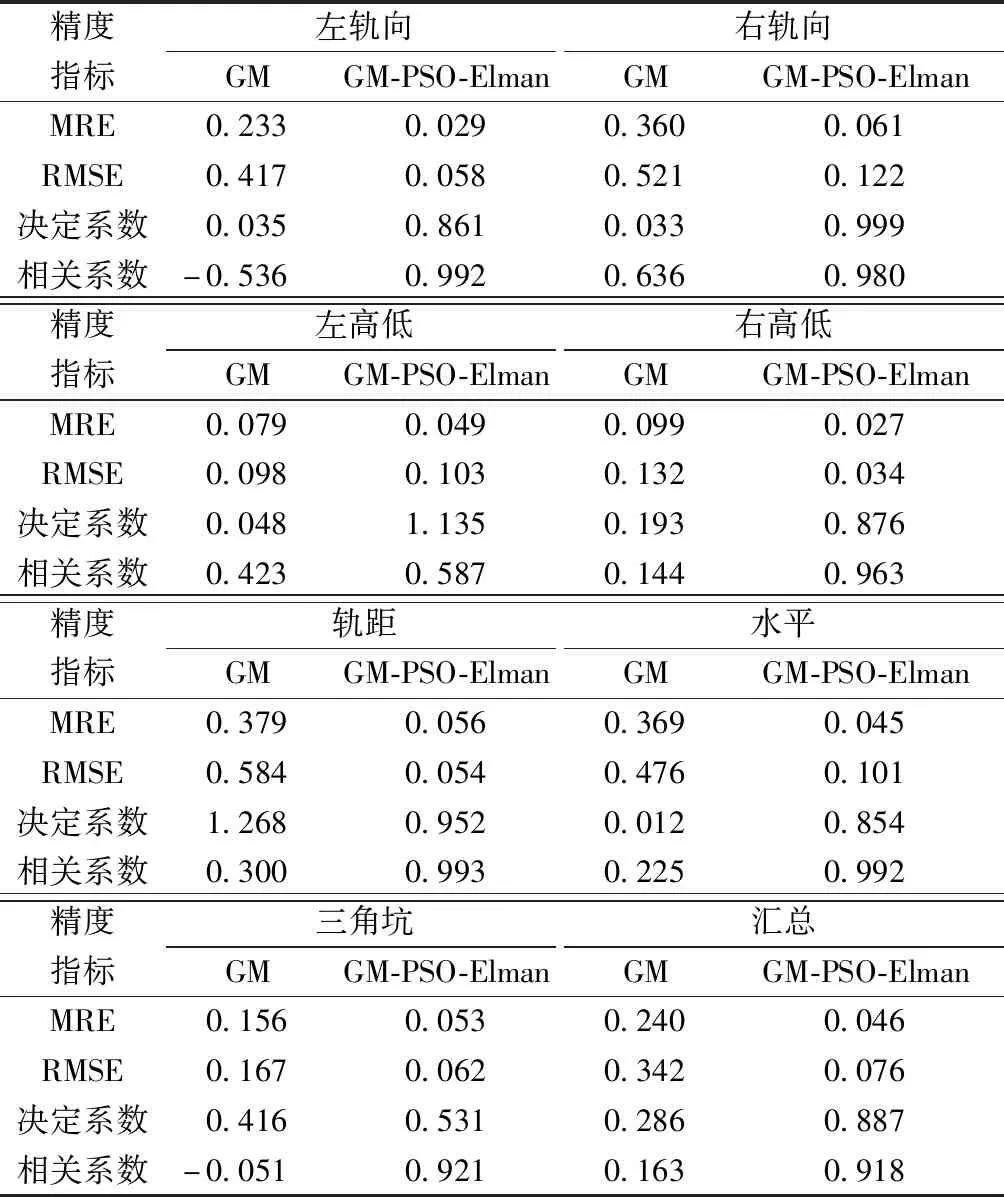
表3 各单项标准差的2种预测方法评价指标

从预测结果的评价指标可以得出如下结论。

(1)从不同模型来看,单一GM(1,1)模型预测精度较低,最后结果中各项的平均相对误差为0.240,均方根误差为0.342,决定系数为0.286,相关系数为0.163,采用粒子群算法对Elman神经网络的参数进行寻优,通过PSO-Elman对灰色模型进行残差校正,预测的各项平均相对误差为0.046,均方根误差为0.076,决定系数为0.887,相关系数为0.918。改进的组合预测方法的稳定性和预测精度有明显提高,这从一定程度上说明残差校正模型可以更好地提高灰色模型的预测精度,整体来讲组合模型的预测精度和鲁棒性要更好。

(2)从单项指标的预测结果来看,组合预测模型的平均相对误差都不高于6.5%,这也很好地说明了该模型的泛化能力,可以根据不同序列的数据信息调整自身的属性,可以适应不同的环境。对于实际的轨道养护维修来说,90%以上的准确率能够满足日常预警维护的需要,也就是说该模型可以对线路不平顺状态进行预警。当某单项指标的预测结果出现超限情况时,会提醒维修人员及时检查线路,保证线路正常运行,真正实现状态修。

3 结论

(1)利用光纤光栅传感器对轨道不平顺数据进行监测,将实际监测数据运用数理统计的方法进行权重分析,确定轨道的左右轨向以及水平这三项指标应作为日常维护的重点检查项目,对各单项指标和TQI指标的超限分析来判断线路的状态,以有针对性地指导列车调度作业和轨道检修作业。

(2)根据轨道状态数据的变化特征建立GMPSO-Elman组合预测模型,对区段内各单项指标的标准差进行预测,新方法不仅具有传统单一预测方法简单适应的特点,还能充分解决数据序列的趋势性和随机性,结果表明该模型具有较高的预测精度,能够实现对下一时间段轨道状态的预警。

(3)为轨道状态的监测预警提供了新的思路,对轨道不平顺动态养护具有一定的参考价值,同时也是开发和研究轨道质量检测系统的关键性技术,可帮助管理者选择针对性的维修方式。由于实验监测数据样本较少,对轨道质量的预测预警是针对短期的、局部的不平顺状态,以后的工作中应收集多时间段的数据,可以实现长期的、整体的轨道不平顺状态预测预警,提高地铁运营的整体安全性能。