四线隧道密贴下穿既有车站施工参数优化分析

2020-09-04高太平闫建龙申健昊李昊炎沈宇鹏

铁道标准设计 2020年9期

高太平,闫建龙,申健昊,李刚,李昊炎,沈宇鹏

(1.中铁四局集团有限公司第三建设有限公司,天津 300011； 2.北京交通大学土木建筑工程学院,北京 100044)

引言

近年来，各大城市都在如火如荼地建设城市轨道交通系统，地铁由于其运量大、对环境污染小、速度快等优点而成为城市轨道交通的先驱[1]。随着地铁线网越来越密集，新建线路和既有线路的交叉穿越已成为必然。地铁穿越工程由于其施工复杂且引起的既有线沉降变形较大，而在《北京市轨道交通工程建设安全风险技术管理体系》中被列为唯一的“特级环境风险工程”[2]。在区间隧道下穿既有车站工程中，为达到“零距离”密贴下穿的目的，区间隧道多采用平顶直墙形式[3]。然而，由于其不利于形成土拱，初支拆除、二衬施作过程中结构受力转换相对复杂，施工具有较大难度和风险，易引起既有结构产生较大沉降变形。选择合理的隧道施工参数控制既有结构的沉降变形是十分必要的[4～7]。

近年来，大量学者对隧道施工参数优化进行了深入研究。许金华等[8]依托工程实例，采用现场试验和数值模拟的方法，以开挖后隧道变形及支护结构受力为评价指标，对不同开挖进尺工况进行对比分析，确定了合理的开挖进尺。许有俊等[9]以北京某地铁上穿工程为背景，以现场监测、数值模拟、理论分析相结合的方法，研究了不同导洞开挖顺序对既有结构的影响，确定了最合理的导洞开挖方案。李涛等[10]以北京某洞桩法车站施工为工程背景，分析不同掌子面错距对地表沉降的影响，最终确定了最优掌子面错距为4 m。王渭明等[11]以青岛某车站施工为背景，将现场监测和数值模拟相结合，以支护结构的应力、应变为评价指标，对不同支撑拆除长度进行对比分析，得到了安全最大拆除距离为6 m。孟令志[12]对某大断面平顶直墙密贴下穿既有线工程进行深入研究，形成了一整套大断面平顶直墙下穿既有线风险控制技术，为类似工程提供一定参考。

目前，对于隧道施工参数优化的研究已经取得极大进展。然而，研究对象大多仅仅是地铁车站以及区间隧道工程，对地铁下穿工程中隧道施工参数优化研究较少，而且依托工程实例大多是洞桩法车站以及双侧壁导坑法隧道，对于大断面平顶直墙隧道研究尚不充分。

本文依托北京地铁19号线四线隧道密贴下穿既有4号线新宫站工程，采用Midas/GTS有限元软件对下穿全过程进行数值模拟，并将模拟结果与现场监测数据对比，验证数值模拟的可靠性，提出不同隧道开挖方案下既有结构的沉降变形特征。同时，对比分析了不同隧道施工参数的沉降差异，在控制既有结构沉降变形的前提下，结合施工速度等要求，确定最优的隧道施工参数。

1 工程概况

北京地铁19号线新发地站至新宫站四线隧道密贴下穿既有4号线新宫站项目，区间正线在中间，共有3种断面形式，A断面位于东侧，采用拱顶直墙大断面施工；下穿段(即B断面)为大断面平顶直墙法施工，下穿长达47 m，断面高约8.36 m，宽约13.5 m；C断面位于西侧，为两个拱顶直墙断面。出入段左右线位于区间正线两侧，断面为马蹄形，高约7.07 m，宽约7.08 m，下穿既有线段采用上下导洞法施工。其中，区间正线及既有站底板之间净距仅为0.22 m，可视为“零距离”密贴下穿。下穿段区间正线及出入线断面如图1及图2所示。

图1 下穿段区间正线断面(单位：mm)

图2 下穿段出入线断面(单位：mm)

既有地铁新宫站为地下双层明挖六跨五柱框架结构，建设年代为2010年。车站总长度360.15 m，宽度为40.9 m，底板埋深约16.58 m，顶板平均覆土厚度约3.2 m，顶板厚0.7 m，底板厚0.8 m，边墙厚0.7 m。新宫站东、西两侧布设φ1 m间距1.6 m的围护桩，围护桩长23 m，混凝土强度等级为C35，新建隧道开挖之前对部分围护桩进行破除，破除长度为6 m。

穿越工程平面及横断面如图3、图4所示。

图3 穿越工程平面

图4 穿越工程横断面

本工程所处区域为北京地区典型的上软下硬地层，从上至下依次分布着杂填土、砂质黏土、黏质粉土、粉细砂、卵石圆砾等地层。新建隧道围岩主要是卵石圆砾，在下穿段隧道开挖之前对隧道轮廓线之外一定范围内进行全断面深孔注浆加固地层。根据相关的勘察资料，本工程不考虑地下水位的影响。

2 评价指标

新建隧道拱顶与既有站底板之间净距较小，故隧道施工过程中极易对既有站周围土体造成扰动，进而引起既有轨道结构不平顺、既有车站产生较大沉降变形。轻则降低乘客舒适性，严重时会影响既有线的正常运营[13]。为控制施工过程中既有结构的沉降变形，相关地铁运营机构出台了一系列规范。根据《北京轨道交通工程建设安全风险技术管理体系》中的相关规定，将各项变形限值整理如表1所示。

表1 地铁结构及轨道变形控制指标 mm

根据表1的规定，在不超出限值的前提下，选取既有站底板的沉降变形作为各项施工参数如导洞开挖顺序、开挖进尺、掌子面错距的评价标准。

3 隧道施工参数分析

3.1 模型建立

根据圣维南原理，地下工程数值计算模型范围一般取隧道开挖跨径的3～5倍[14]，考虑到本工程隧道开挖对既有站周围土体的扰动，确定整体模型X方向(即隧道开挖方向)长度为47 m，Y方向(垂直于隧道开挖方向)长度为120 m，高度为40 m。整体模型如图5所示，既有站与新建隧道相对位置关系如图6所示。

图5 整体模型(单位：m)

图6 既有站与新建隧道相对关系

根据现场地勘资料，土层可分为8层，均采用摩尔-库伦本构模型。既有站顶板、侧墙、中楼板、底板以及隧道初支、二衬、仰拱等均采用二维板单元模拟，既有站柱、围护桩采用一维线单元模拟，对围护桩底部施加约束限制其RZ方向的旋转，所有支护结构均采用线弹性本构。模型涉及的土层及结构物理力学参数如表2所示。模型顶部为自由边界，对于侧面及底面均施加法向约束限制其移动。

表2 地层及模型材料力学参数

3.2 施工步序

本工程隧道截面可进行如图7所示的划分。

图7 隧道截面划分示意

按照相关设计资料，本模型共设置60个施工步骤，大体上可进行如下划分。

阶段一(步骤1)：设置初始应力场并位移清零。

阶段二(步骤2～步骤12)：破除下穿段区间正线东、西侧围护桩，开挖下穿段1、2导洞土体并及时施作初支。

阶段三(步骤13～步骤21)：下穿段区间左线二衬施作。

阶段四(步骤22～步骤31)：开挖下穿段3、4导洞土体并及时施作初支。

阶段五(步骤32～步骤40)：下穿段区间右线二衬施作。

阶段六(步骤41～步骤51)：破除下穿段出入段左右线东、西侧围护桩，开挖下穿段5，6，7，8，9，10导洞土体并及时施作初支。

阶段七(步骤52～步骤60)：下穿段区间中线及出入段左、右线二衬施作。下穿施工完成如图8所示。

图8 下穿施工完成

3.3 模型验证

为验证数值模拟的可靠性，选取下穿施工完成后区间正线隧道拱顶沉降以及围护桩水平位移为两个指标进行对比分析(图9、图10)。

图9 隧道拱顶沉降模拟值与实测值对比

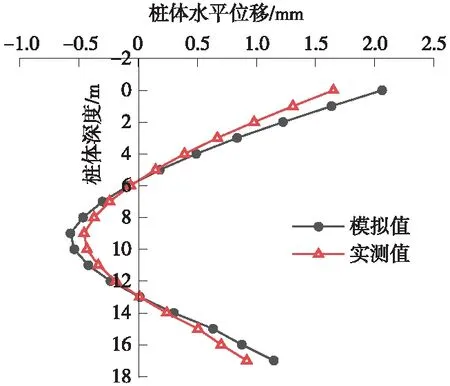
图10 围护桩水平位移模拟值与实测值对比

由图9、图10可得，隧道拱顶沉降与围护桩水平位移模型模拟值稍大于现场实测值，两者数值虽不完全吻合，但误差在可接受范围内且具有相同的变化趋势，由此验证了数值模拟的可靠性，为进行隧道施工参数优化提供了可靠依据。

3.4 结果分析

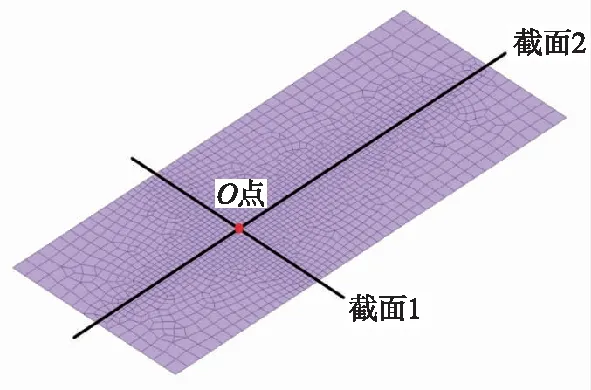
图11 典型截面位置

为了便于分析既有站结构的沉降变化特征，在既有站底板上分别沿隧道开挖方向及垂直于隧道开挖方向选取典型截面。其具体位置如图11所示。其中，截面1为区间隧道中线在既有站底板上对应位置，截面2为既有站底板长度方向中位线，O点为两截面在既有站底板上的交点。

3.4.1 导洞开挖顺序

本工程下穿段为四线隧道，导洞数量较多，在开挖时容易产生“群洞效应”[15]而使得既有站产生较大沉降。为研究不同导洞开挖顺序下既有结构的沉降变化特征以及确定最优的导洞开挖顺序，设置如表3所示的工况进行数值模拟，并对结果进行分析对比。

表3 导洞开挖顺序工况

图12是隧道下穿过程中，上述6种工况下既有站底板O点沉降变化曲线。分析曲线可得，先上后下开挖导洞引起O点发生隆起变形，且3种工况沉降变化曲线具有相同的变化趋势；先下后上开挖导洞引起O点发生沉降变形，且3种工况沉降变化曲线具有相同的变化趋势。然而，先下后上开挖导洞施工过程中既有站沉降超过3 mm的限值。

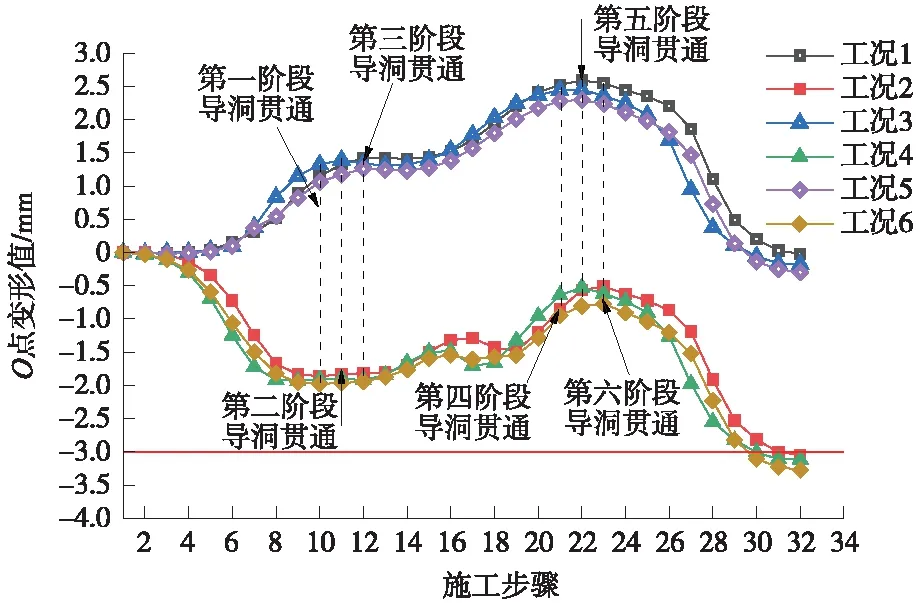
图12 不同导洞开挖顺序既有站底板变形曲线

图13 不同导洞开挖顺序截面1沉降槽

图13及14分别是不同工况下穿施工完成既有站底板截面1及截面2沉降槽。分析两曲线可得，先上后下开挖的3种工况和先下后上开挖的3种工况分别有相同的变化趋势。先下后上开挖导洞引起的既有站沉降超过了3 mm的限值，且工况1(先上后下，先边后中)开挖导洞引起的既有结构的沉降最小。由此可确定工况1(先上后下，先边后中)可以有效抑制群洞效应，先上后下，先边后中是最合理的导洞开挖顺序。

图14 不同导洞开挖顺序截面2沉降槽

3.4.2 开挖进尺

参考Terzaghi松散介质平衡理论[16-17]对开挖进尺的合理范围进行计算,以确定开挖进尺的模拟工况。其计算公式为

式中，b为隧道开挖进尺；c为土体黏聚力；φ为土体内摩擦角；γ为土体重度；q0为地面超载；l1为隧道截面宽度；h为隧道埋深。

经计算，得到合理开挖进尺b=1.86 m。考虑到本工程区间隧道采用CRD法开挖且进行深孔注浆预加固，上式计算结果偏于安全，故设置如表4所示的不同工况进行数值模拟，并将模拟结果进行分析对比。

表4 隧道开挖进尺工况

图15及图16分别是不同工况下穿施工完成后既有站底板截面1及截面2沉降槽。分析曲线可得，不同开挖进尺下既有结构沉降变化曲线具有大致相同的变化趋势。随着开挖进尺的增大，既有结构的沉降变形逐渐增大。分析原因是开挖长度越长，初支封闭时间越长，造成围岩暴露使得隧道变形增大，故隧道开挖应遵循“短进尺”的原则。工况7(开挖进尺为1.5 m)引起的既有结构的沉降变形最小，然而，其结果与2 m的开挖进尺引起的既有结构沉降差别不大，考虑尽可能加快施工速度，施工进尺选取2 m为宜。

图15 不同开挖进尺截面1沉降槽

图16 不同开挖进尺截面2沉降槽

3.4.3 掌子面错距

在已确定开挖进尺为2 m的基础上，为研究不同掌子面错距下既有结构的沉降变化特征，选取掌子面错距为2 m的整数倍，考虑施工进度的安排其值不宜过大。设置如表5所示的不同工况进行数值模拟，并将模拟结果进行分析对比。

表5 掌子面错距工况

图17是隧道下穿过程中，上述4种工况下既有站底板O点沉降变化曲线。分析曲线可得，4种工况沉降变化曲线具有相同的变化趋势，既有结构沉降集中发生在区间中线二衬施作过程中。

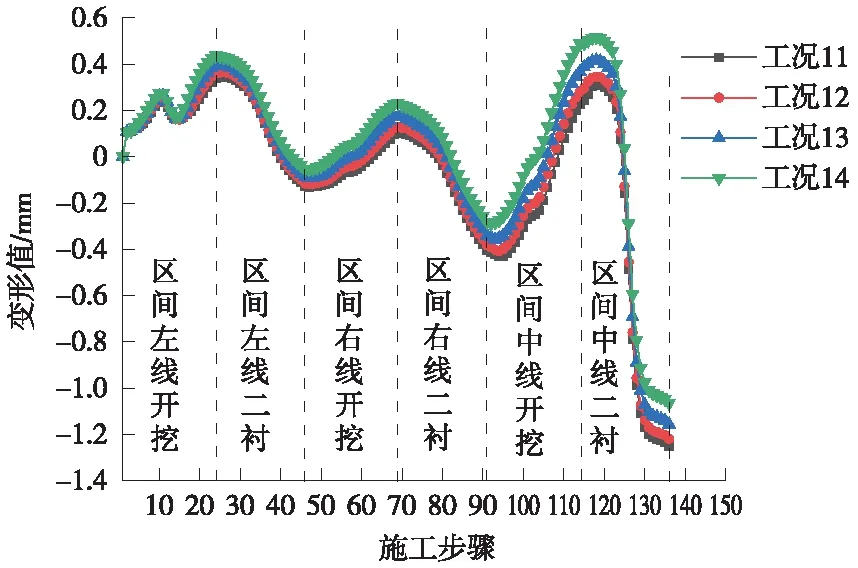
图17 不同掌子面错距既有站底板变形曲线

图18 不同掌子面错距截面1沉降槽

图18及19分别是不同掌子面错距下穿施工完成后既有站底板截面1及截面2沉降槽。分析曲线可得，不同工况的沉降槽变化趋势一致。随着掌子面错距的增大，既有结构沉降逐渐减小。分析原因是掌子面错距越小，上下导洞开挖产生的叠加效应越大，增大掌子面错距，待先开挖导洞稳定后再进行下导洞开挖，可以有效削弱开挖产生的叠加效应。然而，掌子面错距越大，施工周期越大。综合考虑施工安全与施工速度，掌子面错距取6 m为宜。

图19 不同掌子面错距截面2沉降槽

3.4.4 临时支护拆除长度

为研究不同临时支护拆除长度下既有结构的沉降变化特征以及确定最合理的临时支护拆除长度，在对相关工程实例[18-20]深入研究的基础上，结合本工程设计资料，设置如表6所示的不同工况进行数值模拟，并将模拟结果进行对比分析。

表6 临时支护单次拆除长度工况

图20是隧道下穿过程中，上述4种工况下既有站底板O点沉降变化曲线。分析曲线可得，随着临时支护单次拆除长度的增加，施工步骤逐渐减少。4种工况沉降变化曲线具有相同的变化趋势，既有结构沉降变形集中发生在最后几步，即区间中线二衬施作过程中。

图20 不同临时支护拆除长度既有站底板变形曲线

图21 不同临时支护拆除长度截面1沉降槽

图21及图22分别是不同工况下穿施工完成后既有站底板截面1及截面2沉降槽。分析曲线可得，不同临时支护单次拆除长度下既有结构沉降变化曲线具有大致相同的变化趋势。随着临时支护单次拆除长度的增大，既有结构沉降变形逐渐增大，分析原因是临时支护单次拆除长度越大，对新建隧道周围土体产生的扰动越大，从而使得新建隧道拱顶及洞身产生了较大的收敛。欲控制既有结构的沉降变形，应尽可能减小临时支护单次拆除长度。然而，单次拆除3 m及6 m引起的既有结构沉降相差不大，且考虑到单次拆除3 m会增大施工周期，故确定临时支护单次拆除长度取6 m为宜。

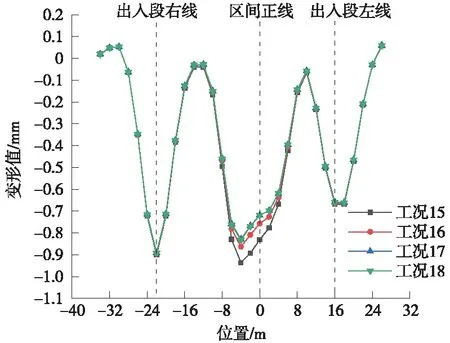
图22 不同临时支护拆除长度截面2沉降槽

3.4.5 有无围护桩

为研究既有站东西两侧围护桩对控制施工过程中既有站沉降变形起到的作用，控制施工参数(开挖进尺、掌子面错距、临时支护单次拆除长度、导洞开挖顺序)不变，分别对有无围护桩两种工况进行数值模拟，并将模拟结果进行分析对比。

图23是隧道下穿过程中，有无围护桩两种工况既有站底板O点沉降变化曲线。分析曲线可得，两种工况沉降变化曲线具一致的变化趋势。且可很明显看出，有围护桩工况下既有结构沉降变形更小。

图23 有无围护桩既有站底板变形曲线

图24及图25分别是上述两种工况下穿施工完成后既有站底板截面1及截面2沉降槽。分析曲线可得，有无围护桩两种工况既有结构沉降变化曲线具有大致相同的变化趋势。若不设置围护桩，则既有结构沉降超过3 mm的限值，而若设置围护桩，既有结构沉降减少了16%，可见既有站东西两侧围护桩对于控制下穿过程中既有站沉降发挥了很大作用。