基于MATLAB的二自由度和四自由度汽车振动模型分析

金琦珺，罗 骞

（武汉理工大学 汽车工程学院，湖北 武汉430070）

1 引言

机械振动对于人类的生产生活来说是一把双刃剑，既可以服务于人类，又对人类的生产活动有重大危害。机械振动既有有利的一面也有有害的一面。需对振动进行动态分析，通过研究物体偏离平衡位置的位移、速度、加速度等的动态变化来达到目的。在物体的平衡点附近出现的物体的来回运动，有线性和非线性两种振动模式。由于外界对系统的激励或作用，使得机械设备产生噪声及有损于机械结构的动载荷，从而影响设备的工作性能和寿命。尤其是发生共振情况时，可能使机器设备受到损坏，所以急需对机械振动的相关原理进行研究。为了合理减小振动对设备的危害，充分利用振动进行机器运作，对机械振动产生的规律进行了探讨和研究。随着计算机智能系统的快速发展，相关的仿真技术都出现了极大的提升空间，在日常的生产活动中，人们经常用到的相关软件有adams、abaqus等。目前MATLAB计算机软件在计算机的仿真方面使用更加广泛一些，MATLAB是一款拥有强大绘图能力的工程计算高级计算机语言。

2 建立数学模型

数学模型是将数学的推理逻辑和相关语言相融合在一起的高级数学工程模型，它建立在事物的系统特征和数量关系模型之上，运用被人所可以认知的数字语言，概括总结出某种相关系统的关系模型。从被人所熟悉的角度理解为，数学模型就是数学学习中常见的各种公式定理。又因为数学来源于日常生活中的各种原型事物，所以又可以理解为数学就是一门关于数学模型的数字科学理论。从不被人理解的角度看，数学模型反映的只是一些特定问题和数字结构，数学模型就是一个系统结构间的数字表达。数学模型包括线性和非线性两种，线性模型即各数学量之间拥有的关系是线性的，可以将各方数字量进行叠加处理，可以理解为输入量的同时作用力与输出量的单独作用力相等。线性模型结构简单，在生活中的应用更加广泛。非线性模型所表达是各系统量之间的关系是散乱的，没有固定的规律可循，也不能直接叠加。然而在某些条件满足的情况下，非线性与线性之间的分界线就会破裂，可以实现非线性到线性的转化。具体表现为将非线性模型在允许的领域内展开成泰勒系数，再留下一阶项，同时将高阶项省略，从而得到线性模型。而本文所要研究的车辆悬挂就属于非线性的模型数据。要想进行系统的仿真处理，就必须学会如何建立数学模型，因为一切计算机软件都建立在数学模型的架构基础上。

二自由度和四自由度的数学模型分别如图1、图2所示。图1中k1为悬架刚度，c为悬架阻尼，k2为轮胎刚度，m2为车身质量，m1为轮胎质量。

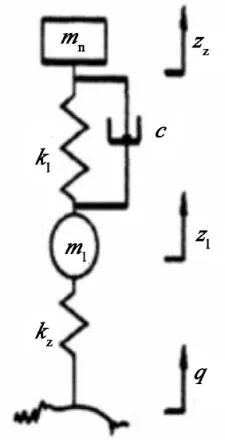
图1二自由度数学模型

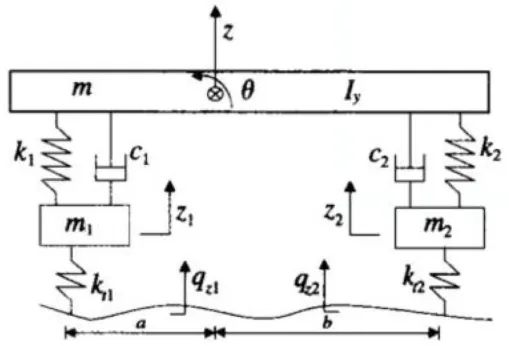
图2四自由度的数学模型

3 二自由度系统振动的模拟

3.1 微分方程的建立

根据牛顿第二定律建立其微分方程如下：

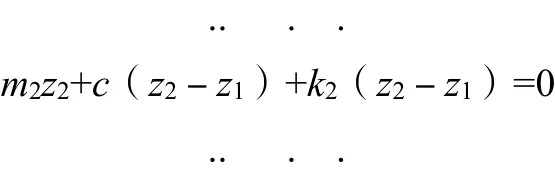
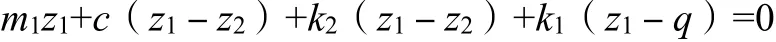
取状态向量：

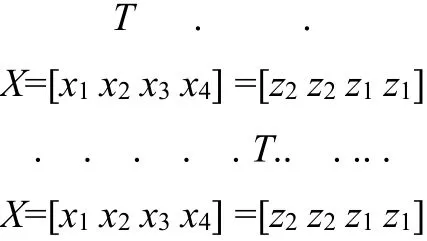
取输入向量u=[q]，输出向量：

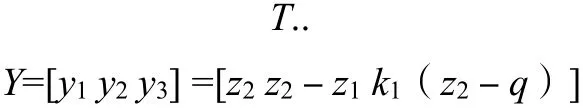
代入系统运动微分方程得其状态方程：

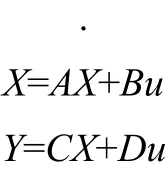
可以得出A、B、C、D。

3.2 系统仿真模型的建立

利用MATLAB软件强大的计算分析，可以较好地分析振动情况，解决实际问题，根据所推导出的二自由度系统振动运动学方程，并运用MATLAB编程绘制出二自由度系统受迫振动的运动轨迹曲线，程序如下：

其Simulink图如图3所示。计算结果如图4所示。

通过分析可以看出，运用MATLAB编程求出的二自由度无阻尼振动系统的运动轨迹曲线是符合要求的，从而验证了该模型仿真结果的正确性以及二自由度无阻尼振动系统的振动规律的客观性。

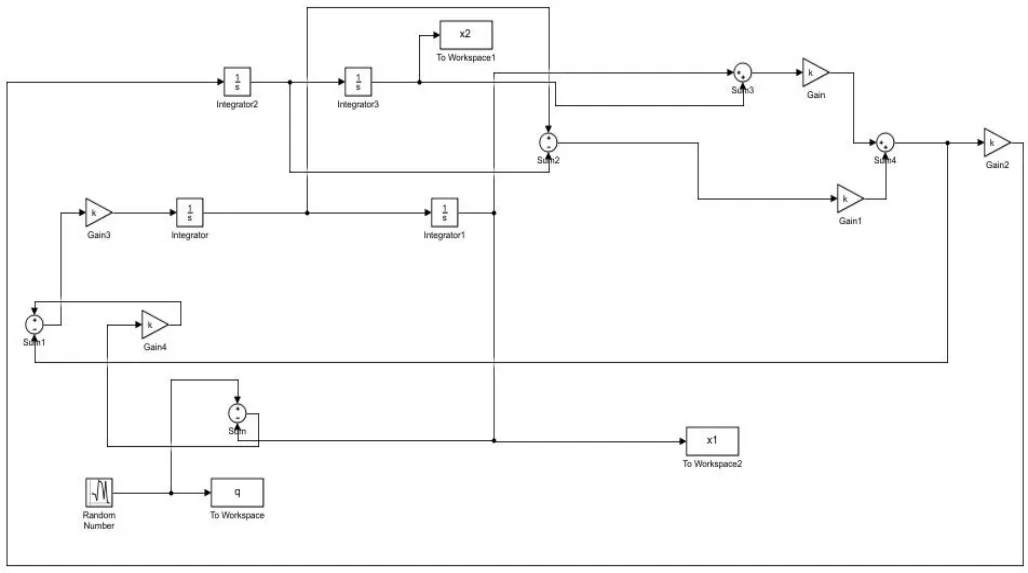
图3 Simulink图

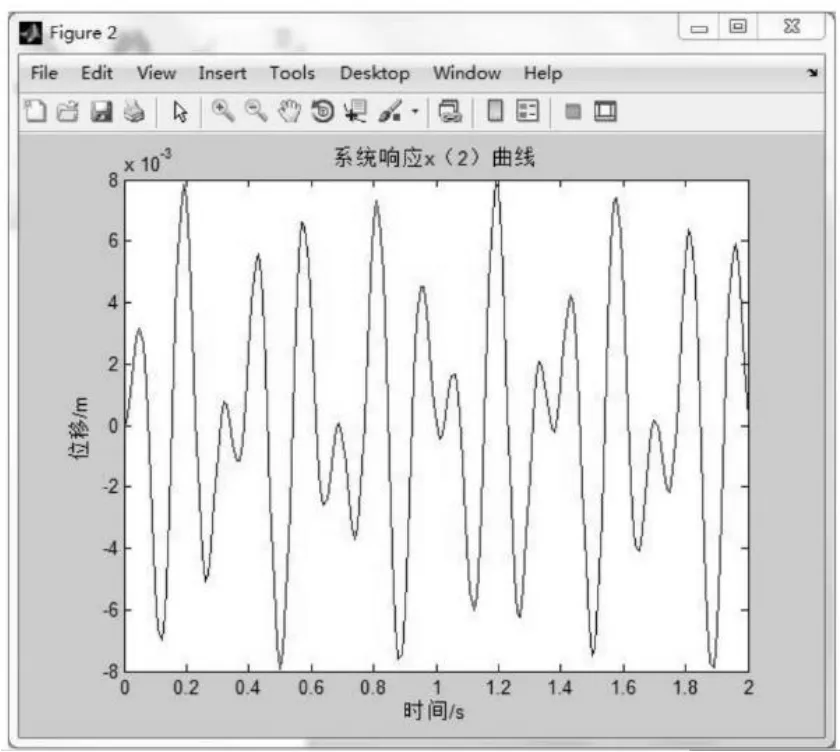
图4计算结果

4 四自由度系统的仿真

图2中，m1、m2分别为前、后车轮的簧下质量，kg；m3为车体（悬挂）质量；k11、k12为前/后轮胎等效刚度，N/m；k21、k22为前/后悬架弹簧刚度，N/m；c1、c2为前/后减震器的阻尼系数，Ns/m；J为簧载质量绕其质心的转动惯量；q为车体绕其质心的旋转角度；z1、z2为前/后车轮轴的位移；z3为车体质心处的位移；z'1、z'2为车体在前/后悬架处的位移；u1、u2为主动控制力；r为路面激励。其中，z1=z3-qa；z2=z3+qb所以z1=z3-qa；z2=z3-qb。

动学方程：m1z1=k21（z'1-z1）+c1（z'1-z1）-k11（z1-r1）-u1=[k21（z3-z1-qa）+c1（z3-z1-qa）-k11（z1-r1）-u1]，m2z2=k21（z'2-z2）+c2（z'2-z2）-k12（z2-r2）-u2=[k22（z3-z2+qb）+c2（z3-z2-qb）-k12（z2-r2）-u2]，m3z3=k21（z'1-z1）-c1（z'1-z1）-k22(z'2-z2)-c2（z'2-z2）+u1+u2=k21（z3-z1-qa）-c1（z3-z1-qa）-k22（z3-z2+qb）-c2（z3-z2+qb）+u1+u2。

其仿真如图5所示。路面模型的建立如图6所示。仿真结果的分析如图7所示。

4.1 悬架阻尼系数C的影响

在保持一定量数据不变的情况下，变化前悬架的相关阻尼数据，C2f系统仿真效果如图7所示。因为车身存在固定的频率1～2 Hz，所以可以得到如图7所示的低频段考虑，在1～2 Hz的周围随着阻尼系数的不断增长，车身的整体质心位移角度不会出现太大的变化。然而从整体的车身结构来看，在适当的位置增加悬挂系统可以有效增强车身的整体稳定系数。同样，在其他条件不出现改变的情况下，改变后悬架系统的阻尼数据C2R，结果如图7所示。由图7可以得知，通过增加后悬架系统的阻尼数据，在1～2 Hz的周围，车身的整体质心没有较大变化，而仰角出现了较大的改变，在阻尼数据继续增加的情况下，车身质心振幅的增大带来的是仰角趋于平稳，因此可以发现，阻尼数据的缩小对车身振幅的改变有较大作用。因此，通过适当缩小后悬架系统的阻尼数据可以增加汽车整体的平稳性。

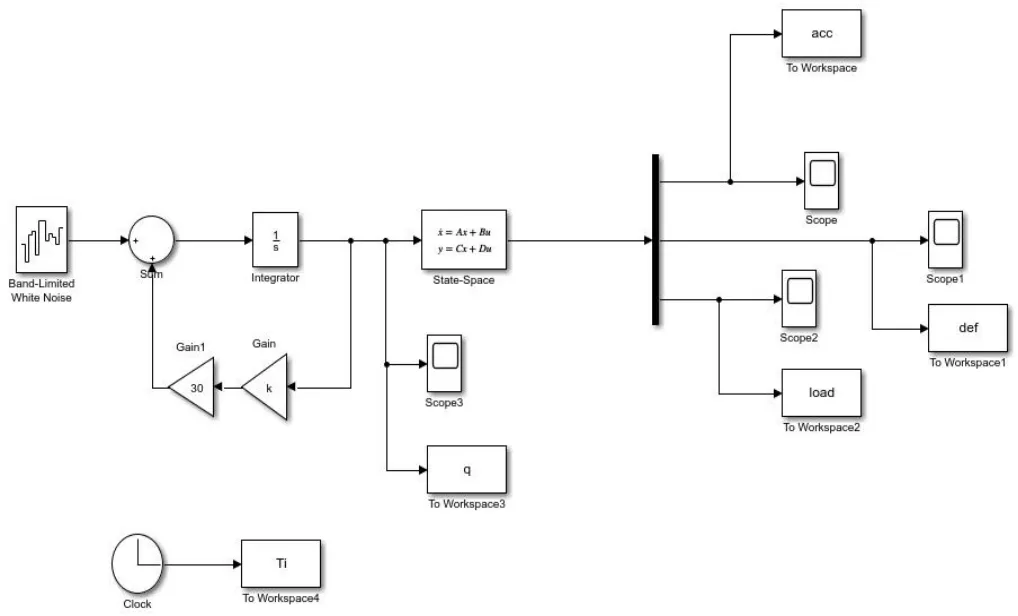
图5仿真情况

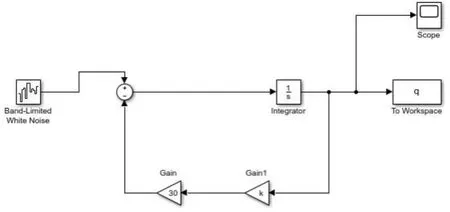
图6路面模型的建立

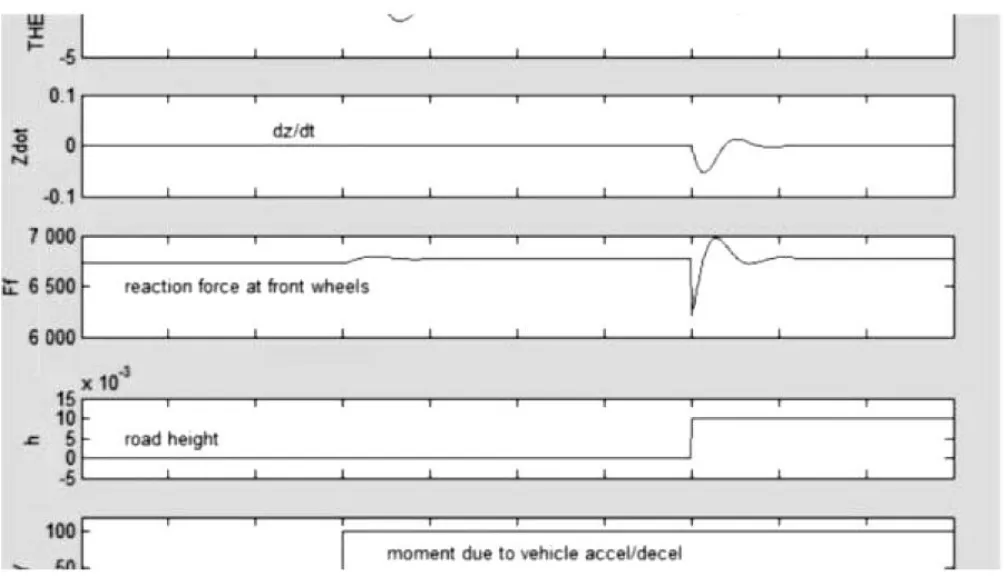
图7仿真结果的分析

4.2 悬架刚度系数K的影响

由数据模拟结果可以看出，在加大前悬架的刚度数据的情况下，在辨别的1～2 Hz周围，车身的整体质心位移不会出现太大的变化，而仰角的幅度会有所增加，同时在2～3 Hz的周围，车身的质心和仰角会随着数据的变化而增大，因此，在设计车身时要注意适当调整前悬挂架，进行适当缩小。

同时考虑后悬挂架的相关数据模型，在1～2 Hz周围可以观察到车身的质心有较大的偏移，而仰角却缩小。因此，从驾驶安全的角度考虑，需要适当扩大后悬挂的刚度数据。

4.3 轮胎刚度系数K1的影响

同时要关注轮胎的刚度数据，相关的模拟结果如图4所示。由相关的数据结果表明，轮胎给车身质心变化带来的影响非常小，轮胎的刚度数据的缩小会使悬挂架的变化增大，同时仰角缩小，但此时带来的是轮胎载重数据的缩小，所以在对前轮胎进行修正时，不要充气太足。

在相关数据没有改变的情况下，通过调整后轮胎的刚度数据来进行实验，如图7所展现，在1～2 Hz周围，当Kr1增加时，车身的质心垂直的加速度数值变化非常小，同时仰角度数会有一定减小，然而这对于车身振动性质的改变很有帮助。

通过分析不难发现，四自由度的MATLAB仿真模型符合要求，从而验证了该模型仿真结果的正确性以及四自由度无阻尼振动系统的振动规律的客观性。可以得出：增大前悬架的阻尼数据，同时缩小后悬架的阻尼数据可以让汽车的整体平稳性得到提高；在前悬架系统的设计制造中，可以对其刚度数据进行适量缩小，同时可以通过提高后悬架系统的刚度来增加汽车的安全性；前轮胎的刚度数据变化对于车身的影响非常小，所以在车身整体的调节过程中，可以通过对后胎的调整来增加驾驶员的舒适性。

5 结论

通过对MATLAB编程工具的有效运用，可以充分模拟机械振动所产生的各项数据模型，让整体的数据模型架构过程都得到有效提升，大大节省了时间，提高了效率。

同时运用MATLAB软件验证了该模型的正确性和客观性，通过MATLAB仿真软件的联合仿真进行分析，得到仿真结果：二自由度无阻尼振动系统在激振力作用下受迫振动随着固有频率的改变，在一定条件下产生共振。因此，为了合理改善和利用机械振动，对实际工程中的机器设备的研究具有参考价值。