浅谈初中数学几何概念的引入

马慧民

恩格斯说：“在一定意义上，科学的内容就是概念的体系”。可见数学概念的学习是学好数学的一个首要环节。这些年来的教学实践也表明，数学学习的过程，就是不断地建立各种数学概念的过程。几何概念反映的是图形的空间形式和数量关系及其属性，正确理解和掌握几何概念是进行推理、判断和证明的关键，只有理解和掌握了数学概念，才能进一步进行问题的探讨论证。而引入概念是学好概念的关键，下面仅以这几年的教学实践谈谈几何概念的几种引入方法。

一、由已有或已知的概念引出新的概念

例1：由“三角形中位线”引出“梯形中位线”

在“梯形中位线”教学中，先引导学生复习回顾“三角形中位线”的概念，指出“三角形中位线”是两条边中点的连续，三角形中位线上的点到第三边的距离等于第三边所对应的顶点到中位线的距离。然后提出问题“梯形对边中点的连线上的点是否和三角形中位线上的点具有相似的性质呢？梯形对边中点的连线能否也叫梯形的中位线呢？”。由此由“三角形中位线”引出“梯形中位线”的概念。

例2：由“全等三角形”引出“相似三角形”

教学时，通过复习回顾“全等三角形”的概念，强调三角形全等时对应边的比是1，接着提问“当两个三角形的对应边的比不是“1”时，而是“2”或是“3”时，这两个三角形具有怎样的形态特征呢？”，由此引入三角形相似的概念。

同理，我们也可以由“线段的垂直平分线”引出“角平分线”的概念，由“平行四边形”的概念引出“矩形”的概念等。

二、通过观察、体验和抽象现实生活中的实例，引出概念

例3：由杂技“独轮自行车车走钢丝”引入切线的概念

在教学中可以先播放独轮自行车车走钢丝的杂技视频，然后引导学生分析实例，抽象绘制几何图形。独轮车的车圈可看做一个“圆”，钢丝可看做“一条直线”，它们只有一个接触点，可以看做是圆和直线的“交点”。这样我们就可以在这个实例的演示、观察、分析的过程中引入“切线”的概念。

例4：由“天安门城楼”引入“轴对称”，由“铁轨、双杠”引入平行线的概念等。

三、从解决数学实际问题的内部需求出发，引出新概念

例5：由“修建某个扬水电站”引入“三角函数”的概念

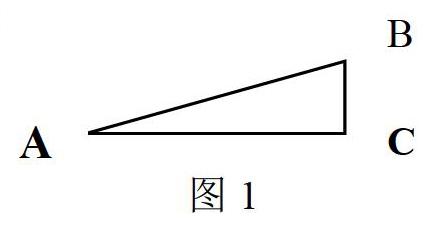
如图1：要修建某个扬水电站，要沿着斜坡铺设流水管道，水管的长度AB可以通过测量得到，水平面与斜坡的夹角也可以测得。但是点C无法到达，线段BC的长度无法直接测得，所以利用已经学得知识不能得到BC的长度，那么怎样计算BC的长度呢？从而引入“三角函数”这个概念。

例6：“三线八角”中“同位角、内错角、同旁内角”的概念的引入也是为了研究不同位置的角的关系而引入的。

四、通过动手等实践活动引出新概念

例7：“三角形重心”的引出

我们可以准备一个形如“三角形”塑料板和一个铁钉，用铁钉把三角形塑料板固定在黑板上（注意不要损坏黑板），找能使三角形塑料块静止不动的铁钉钉的位置点，找出这个点后，观察点的位置，引导学生分别做这个三角形的三个内角的角平分线和三边的中线，看看它们的交点和这个点的位置关系，最后引入“重心”这个概念。

例8：用简易教具演示，引入“直线与圆”的位置关系

教学中，可在黑板上画一个圆，在一根直木棍上拉一根皮筋，皮筋的另外一端固定在圆心处，使木棍和皮筋保持垂直，木棍和皮筋可看做是直线和圆心到直线的距离，然后移动木棍（直线），观察木棍（直线）和圆的位置关系，就可直观得到直线和圆相交、相切和相离等概念。

五、在运用数学知識进行运算、推理和证明的过程中引出新概念

例10：在一条定线段AB上求一点C，使AC是全线段AB与另一部分BC的比例中项。

通过列式计算我们发现C点恰好在AB线段的（√5-1）/2处，即AC等于AB的（√5-1）/2倍。随后引入点C是线段AB的“黄金分割点”的概念。为什么叫“黄金分割”呢？原来这个比例具有美学价值，如果采用这个比例做长方形门窗，看上去使人匀称悦目。舞台上站在这个点唱歌发出的声音会更加悦耳动听。因而“黄金分割”在建筑、绘画、雕塑等方面广泛应用。

例11：通过推理和计算得“邻补角”、“中垂线”、“内切圆”等概念。

总之，几何概念引入的方式方法很多，只要我们灵活合理的引入概念，正确理解和掌握几何概念及其本质属性，注重几何概念在现实生活中的应用，那么就可以为进一步学习数学知识打下坚实的基础，就可以有效提高数学教学质量。