大型空间碎片机械冲击消旋位姿计算方法研究*

张德轩 秦晓刚 杨生胜 侯玮杰 马 睿 张慧博 戴士杰

1.河北工业大学机械工程学院，天津 3001302.兰州空间技术物理研究所真空低温技术与物理重点实验室，兰州 7300003.天津市微低重力环境模拟技术重点实验室，天津航天机电设备研究所，天津 300458

0 引言

空间碎片是指人类在空间活动中遗留在空间中的废弃物，其中包括火箭发射过程中脱落的火箭末级、失效卫星、空间碰撞物等，由于其失去了姿态调整能力而成为空间非合作目标。近年来由于空间活动次数的增加导致空间碎片数量增加，如果不进行回收处理将导致大量空间非合作目标滞留在太空中，进一步增加了航天器在空间轨道中的碰撞风险。美国国家航空航天局的研究人员指出：为保持空间环境可持续发展，未来发射航天器除了要进行任务后处理外，每年还要主动清理5个以上的大型航天器才能抑制空间碎片总数量的增长[1-4]。但由于空间非合作目标运动规律复杂，直接进行捕获难度较大，危险性较高，若能在实施捕获前进行消旋处理，将有利于之后的捕获作业[5]。

目前对于大型空间碎片主要有两种消旋方式，接触式消旋和非接触式消旋。文献[6-7]将弹性小球作为机械臂末端执行器，利用机械臂末端与目标表面之间弹性碰撞所产生的推力与摩擦力衰减目标转动，由于没有一种冲击方法的指导，冲击效果有可能会与预期相反。文献[8]研究了利用机器人对非合作目标进行消旋的控制方法，但前提是机器人能够安全地抓取空间碎片，不适用于空间碎片转动速度较快的情况。文献[9]利用减速刷与目标间的弹性接触力在抓捕前对目标进行消旋，但实施前需要服务航天器进行复杂的变轨绕飞，而且也只能针对简单运动的空间碎片进行消旋。文献[10]提出了利用粘弹性绳系附着到旋转非合作目标表面上，通过系绳拉力及变形时的阻尼力控制目标转速直至其姿态稳定的方法，但是绳系机器人消旋在如何避免抓捕失败的同时防止绳系缠绕还需要进一步的研究。文献[11]提出了基于带电体之间库仑力作用衰减目标转速的方法，但对于角动量较大的大型空间碎片来说消旋效率较低。文献[12-15]提出可利用导电目标转动时与外部磁场源之间的相对运动产生的涡流力来衰减目标运动,但相对于冲击力消旋效率较低。

对比接触式消旋与非接触式消旋可以发现，接触式消旋效率较高[16]，所用时间较短，但目前没有理论方法指导消旋过程，导致消旋效果不稳定，可能产生严重后果；非接触式消旋安全稳定，但消旋效率较低，在轨时间较长，容易与其他碎片产生碰撞风险，不利于快速高效的连续作业[17]。本文针对机械脉冲消旋无冲击方法指导这一问题，提出了一种机械冲击位姿计算方法，利用此计算方法选择冲击位姿可以有效解决冲击结果不理想的问题，为机械冲击消旋提供理论指导。

1 运动学建模

本文中消旋的大型空间碎片主要包括：废弃的卫星和运载火箭末级、执行任务中的抛弃物品、脱落的活动部件等[18]。本文中空间碎片的运动学建模考虑了在空间中运动物体的转动、章动和进动。空间碎片在此运动下存在三轴的角动量，但在任一瞬时可以将空间碎片的三轴角动量进行合成。

图1 空间碎片运动学模型

图1符号定义如下：OXYZ为基坐标系；OXLYLZL为角动量坐标系；A、B分别为模型上端面和下端面圆心；P1、P2为冲击位置；l为模型长度；r为模型半径。

图1中角动量坐标系的YL轴为合角动量的方向，本文的消旋机理即利用冲击力形成的力偶矩作用于合角动量方向，使空间碎片的合角动量衰减。为避免在消旋过程中空间碎片产生平动，此运动学模型中冲击位置P1和P2是关于O点中心对称的，机械冲击产生的力最后都以力偶矩的形式作用于空间碎片，不会使空间碎片产生平动。

本文以下述形式的非对称惯量阵为输入，利用式(1)进行运动轨迹计算及仿真，图2为空间碎片端面中点在基坐标系下的运动轨迹，图3为空间碎片绕基坐标系三轴旋转的角速度,图4为空间碎片合角动量方向与空间碎片轴线之间的夹角变化曲线[19]。

(1)

图2 端点轨迹图

图3 三轴角速度变化曲线

图4 夹角变化曲线

2 空间碎片消旋

2.1 建立角动量坐标系，获取封闭轮廓线信息

假设已知空间碎片上各点在基坐标系下的坐标，经过时间t后空间碎片三轴转动的角度分别为[α,β,γ]则根据坐标变换原则可以获得在t时刻空间碎片上各点坐标。使用RPY角描述运动姿态旋转公式如下:

(2)

(3)

上式中：

假设t时刻空间碎片X，Y，Z三轴角动量大小分别为[L1,L2,L3],则可以通过矢量相加的方式得到此时空间碎片合角动量的方向向量，计算公式如下：

L=[1,0,0,]L1+[0,1,0]L2+[0,0,1]L3

(4)

以合角动量的方向作为Y轴方向，建立基于合角动量为坐标轴的坐标系，称之为角动量坐标系。将角动量坐标系XLZL平面与空间碎片模型相交形成一个封闭的轮廓线，获取轮廓线上各点在基坐标系中的三维坐标和各点所在空间碎片位置上的形貌信息。使用P表示空间碎片表面各点在基坐标系下的三维坐标，通过遍历以下公式即可得到空间碎片轮廓线上各点坐标。

P·L=0

(5)

2.2 存在直线的轮廓线上各点冲击受力分析

图5为轮廓线上存在直线的空间碎片运动学模型，轮廓线上的直线在一般在空间碎片的两个端面上，当合角动量的方向垂直于空间碎片轴线时轮廓线形状为长方形，此时轮廓线完全由直线组成。在上述情况下的消旋主要为冲击力消旋，橡胶球的冲击方向平行于角动量坐标系的XZ平面。图6为空间碎片模型的侧视图。

图5 空间碎片模型

图6 空间碎片受力分析

选取轮廓线在端面的部分进行分析，机械冲击方向在角动量坐标系的XZ平面上且指向坐标系中心。冲击力的一个分力与端面垂直，另一个分力与端面平行，由上可知冲击产生的分力计算如下：

F11=F21=Fcosθ

(6)

(7)

上式中：θ为轮廓线上各点与模型轴线夹角；K为常数；σ0为拉伸强度；W为载荷；H为硬度；tanδ为损耗因子；Pc为轮廓接触压力，为复合弹性模量[20]。

分力对空间碎片产生的力偶矩分别为：

T1=LFcosθ·tanθ

(8)

(9)

为防止冲击对空间碎片产生倾覆力矩，需要使T1与T2相等，则需满足如下条件：

(10)

上述条件称为冲击力消旋判定条件，满足上述条件即可采用冲击力进行消旋，冲击力作用方式如图7所示。

图7 轮廓线上受力分析

由图7可知，当机械冲击以此种方式作用在空间碎片上时，冲击力产生的分力都会削减总角动量，在此情况下冲击力起主要消旋作用。

综上所述，可以计算出满足上述条件时冲击对空间碎片产生的扭矩：

(11)

当不满足上述判定条件时需要在轮廓线的曲线部分选点进行冲击，这时可以与2.3节内容共同讨论。

2.3 不存在直线的轮廓线上各点冲击受力分析

图8为轮廓线上不存在直线的空间碎片运动学模型，一般情况下轮廓线形状为椭圆形，当合角动量方向与轴线平行时轮廓线形状为圆形。在上述情况下的消旋主要为摩擦力消旋，橡胶球的冲击方向平行于角动量坐标系的XZ平面。图9为空间碎片受力分析示意图。

图8 空间碎片模型

图9 空间碎片受力分析

选取椭圆轮廓线上长轴对称点进行分析，机械冲击方向在角动量坐标系的XZ平面上且指向坐标系中心。冲击力的一个分力与冲击点表面法向相同，另一分力与冲击点表面平行且为滑动摩擦，由上可知冲击所产生的分力计算公式如下：

F11=F21=Fsinθ

(12)

(13)

分力对空间碎片产生的力偶矩分别为：

T1=2rFcosθ

(14)

(15)

为防止冲击对空间碎片产生倾覆力矩，需要使T1与T2相等：

(16)

图10 轮廓线上受力分析

综上所述，可以计算出满足上述条件情况在冲击时对空间碎片产生的扭矩大小：

(17)

3 仿真实验

NASA空间碎片计划负责人Johnson分析具有潜在威胁的大型空间碎片主要为火箭末级、失效卫星及其解体后的衍生目标，其质量分布在1000～3000kg之间[21]。本次仿真以常见的火箭末级作为消旋目标，可以将其近似成一个规则圆柱体，拥有三轴角动量并失去了姿态调整能力[22]。此次仿真实验中模型半径为1000mm，长度为3000mm，质量为1000kg。

根据空间碎片尺寸数据，分析空间碎片轴线与合角动量之间的夹角与轮廓线形状的关系，见图11。

图11 空间碎片侧视图

3.1 轮廓线上存在直线时的仿真实验

由图4可知在854.6s时空间碎片合角动量方向与空间碎片中心轴线之间的夹角为73.6°，由上可知，轮廓线上存在直线，因此本次仿真采用冲击力与摩擦力联合消旋。

本次仿真中冲击时刻为854.6s，冲击时间为0.4s，假设碰撞力大小为60N，摩擦力为48N。在仿真过程中，姿态控制被禁用，并且忽略了自然干扰力和力矩。仿真步数为10000步，时间为2000s，步长为0.2s。表1为冲击前后空间碎片角动量变化情况，由表中数据可知：空间碎片三轴角动量减小百分比几乎相同，因此可判断合角动量方向不会发生变化，之后的冲击不必再进行辨识作业。

表1 空间碎片冲击前后角动量变化

为了更直观的表达空间碎片运动状态的变化，可以观察其它参数的变化情况。如图12所示为空间碎片三轴角速度的变化曲线,图13为进动角速度变化曲线。可以看到，在冲击前后空间碎片三轴角速度的均值和幅值都有所降低，进动角速度均值同样减小了。空间碎片X轴角速度的均值由2.82(°)/s减小到了1.05(°)/s，减小了62.8%；Y轴角速度的均值由-4.80(°)/s减小到了-1.77(°)/s，减小了63.13%；Z轴角速度的均值由6.24(°)/s减小到了2.29(°)/s，减小了63.30%，进动角速度由8.55(°)/s减小到了3.15(°)/s，减小了63.16%。

图12 三轴角速度变化曲线

图13 进动角速度变化曲线

3.2 轮廓线上不存在直线时的仿真实验

由图4可知在909s时空间碎片总角动量与空间碎片中心轴线之间的夹角为30.73°，经计算，轮廓线上不存在直线，因此本次仿真采用摩擦力消旋。

本次仿真中冲击时刻为909s，冲击时间为0.4s，假设碰撞力大小为60N，摩擦力为48N。仿真步数为10000步，时间为2000s，步长为0.2s。表2为冲击前后空间碎片角动量变化情况。

表2 空间碎片冲击前后角动量变化

图14所示为空间碎片进动角速度的变化曲线，图15为进动角速度变化曲线。可以看到，在冲击前后空间碎片三轴角速度的均值和幅值都有所降低，进动角速度均值同样减小了。空间碎片X轴角速度的均值由2.84(°)/s减小到了2.06，减小了27.46%；Y轴角速度的均值由-4.80(°)/s减小到了-3.47(°)/s，减小了27.71%；Z轴角速度的均值由6.23 (°)/s减小到了4.53(°)/s，减小了27.29%，进动角速度由8.55(°)/s减小到了6.20(°)/s，减小了27.49%。

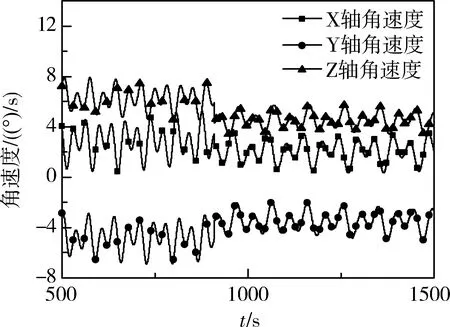
图14 三轴角速度变化曲线

图15 进动角速度变化曲线

4 结论

针对大型空间碎片的消旋问题，提出了一种利用机械冲击进行消旋的消旋策略，建立了空间碎片消旋的运动学模型，分析了机械冲击消旋的作用机理。选定一种常见空间碎片进行了仿真实验，由仿真实验结果可以得到以下结论：1)本文所采用的消旋策略可以同时减小空间碎片的三轴角动量，且冲击过程中合角动量方向不发生变化；2)机械冲击消旋的效率很高,可以在短时间内得到安全的捕获状态；3)冲击力消旋效率远高于摩擦力消旋效率，尽量选择轮廓线上存在直线时进行冲击消旋；4)消旋效率的提升和消旋过程的安全性受制于当前空间碎片位姿辨识精度和消旋卫星末端执行器的控制精度。