主动段姿态控制参数与稳定裕度映射关系研究
2020-09-03吴建武张惠平
吴建武 吴 浩 张惠平
北京航天自动控制研究所,北京 100854
0 引言
稳定裕度[1],包括幅值裕度和相位裕度,是度量控制系统稳定性的重要指标,在工程应用上具有重要的指导意义。关于各类控制系统稳定裕度的研究,特别是稳定裕度的计算[2-4]与在线辨识[5-7]方法,一直是控制理论研究中的一个重要内容。
稳定裕度同样也是各类导弹(火箭)姿态控制系统设计过程中的重要指标。当导弹(火箭)飞行状态和预设值发生偏离时,姿态控制系统稳定裕度将不可避免地与设计结果存在偏差,甚至超出稳定要求,严重时将导致飞行失利。针对这一情况,众多学者提出了提高姿态控制系统对偏差适应能力的方案,这包括从模型着手,如通过辨识风场建立更为精确的被控对象模型的方案[8],以及从控制器着手,如通过鲁棒动态逆[9]、神经网络容错控制[10]、自适应控制[11]、智能控制[12]等的方案。
研究在线辨识姿态控制系统稳定裕度的方法,并基于稳定裕度辨识结果在线调整控制参数,使稳定裕度重新“回到”稳定要求范围之内则是一种最为直接的方案。建立控制参数与稳定裕度之间的映射关系,是实现在线调整姿态控制系统稳定裕度的基础。
鉴于控制参数与稳定裕度之间的映射关系的重要性,本文将针对固体导弹(火箭)主动段姿态控制系统,研究基于解析方式建立控制参数与幅值(相位)裕度映射公式的方法,并利用数学仿真对映射公式的有效性进行验证。
1 被控对象描述
对于固体导弹(火箭)的主动段,影响姿态控制系统稳定裕度的主要因素有导弹(火箭)本体特性、单机特性和控制器特性。由于惯组(平台)的带宽通常远高于伺服机构的带宽,为了简化问题,单机特性方面本文仅考虑伺服机构的特性。考虑到导弹(火箭)的偏航通道与俯仰通道类似,本文只对俯仰通道进行讨论。另外,考虑到固体导弹(火箭)的弹性运动频率一般远高于弹(箭)体的截止频率,本文在对控制参数与刚体稳定裕度映射关系的研究过程中,忽略弹性运动的影响。
1.1 刚体运动模型
固体导弹(火箭)姿态运动刚体部分的传递函数在弹(箭)体静稳定时为[13]:
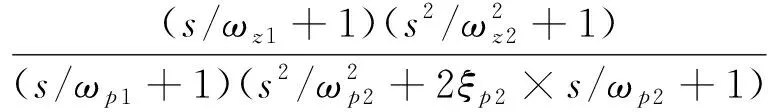
(1)
在弹(箭)体静不稳定时为[13]:
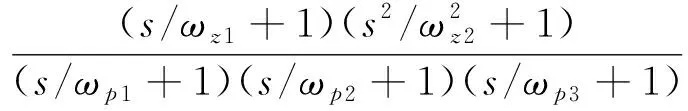
(2)
式中:
k0=(b3fc1f-b3fc2f-b2fc3f)/(b2fc2f),
ωz1=(b3fc1f-b3fc2f-b2fc3f)/b3f,
ωp2=
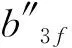
1.2 伺服机构模型
本文按下述传递函数考虑伺服机构特性,
(3)
1.3 控制器构型
本文采用的控制器的传递函数形式为:
(4)
在控制器GC(s)中有ωcp>ωcz。在本文的讨论过程中,忽略离散化过程对控制器幅相特性的影响。
1.4 姿控回路开环幅相特性
考虑导弹(火箭)本体特性、伺服机构特性和控制器特性等因素后,俯仰通道姿态控制回路开环传递函数为
G(s)=-GV(s)GS(s)GC(s)
(5)
在静稳定情形,当满足|ωp2|<ω≪|ωz2|时,或静不稳定情形,当满足max(|ωp2|,|ωp3|)<ω≪|ωz2|时,忽略公式里的小量部分,G(s)的对数幅频特性函数可以近似如下:
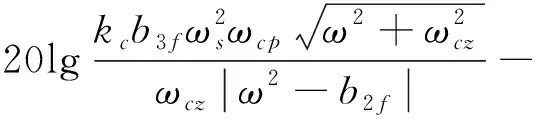
(6)
同理,G(s)的对数相频特性函数可以近似如下:
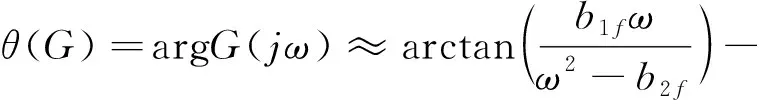
(7)
2 控制参数与幅值裕度的映射关系
2.1 幅值裕度计算
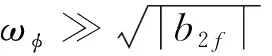
(8)
注意到,ωφ满足ωφ≪ωs,如果在选取控制参数时,使ωcz和ωcp分别满足ωcz≪ωφ和ωcp≪ωφ,那么忽略式(6)中的小量,可以将俯仰通道幅值裕度计算公式进一步化简为:
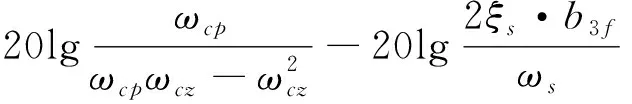
(9)
根据上式,就可以利用导弹(火箭)模型参数(b3f)、伺服机构模型参数(ωs和ξs)、控制器参数(kc,ωcp和ωcz)近似计算俯仰通道幅值裕度。利用Nyquist稳定性判据可知,当-L(G(jωφ))>0时,姿态控制系统稳定,否则系统不稳定。为了使系统稳定并拥有足够的幅值裕度,在设计姿态控制器参数kc,ωcp和ωcz时,需要将式(9)“≈”号的右边设计为恰当的正值。
2.2 控制参数与幅值裕度映射公式
根据式(9),可以分别得到控制参数与幅值裕度的对应关系为:
L1(kc)=-20lgkc
(10)
控制参数ωcp和ωcz与幅值裕度的对应关系为:
(11)
导弹(火箭)模型参数b3f、伺服模型参数ωs和ξs与幅值裕度的对应关系为:
(12)
根据式(10)和式(11),可以直接得到控制参数kc,ωcp和ωcz变化时,对应的-L(G(jωφ))的变化量,即分别建立了控制参数kc,ωcp和ωcz与幅值裕度之间的一种映射关系。从式(10)可以看出,幅值裕度关于kc单调递减。从式(11)可以看出,当差值ωcp-ωcz固定时,幅值裕度关于比值ωcp/ωcz单调递减;当比值ωcp/ωcz固定时,幅值裕度关于差值ωcp-ωcz单调递增;分别以ωcp/ωcz和ωcp-ωcz为x和y轴坐标,可以得到L2(ωcp,ωcz)随控制参数ωcp和ωcz变化的曲面如图1所示。以上单调性表明,当给定幅值裕度的变化量时,可以根据式(10),或者式(11)确定kc,ωcp和ωcz的调节量。
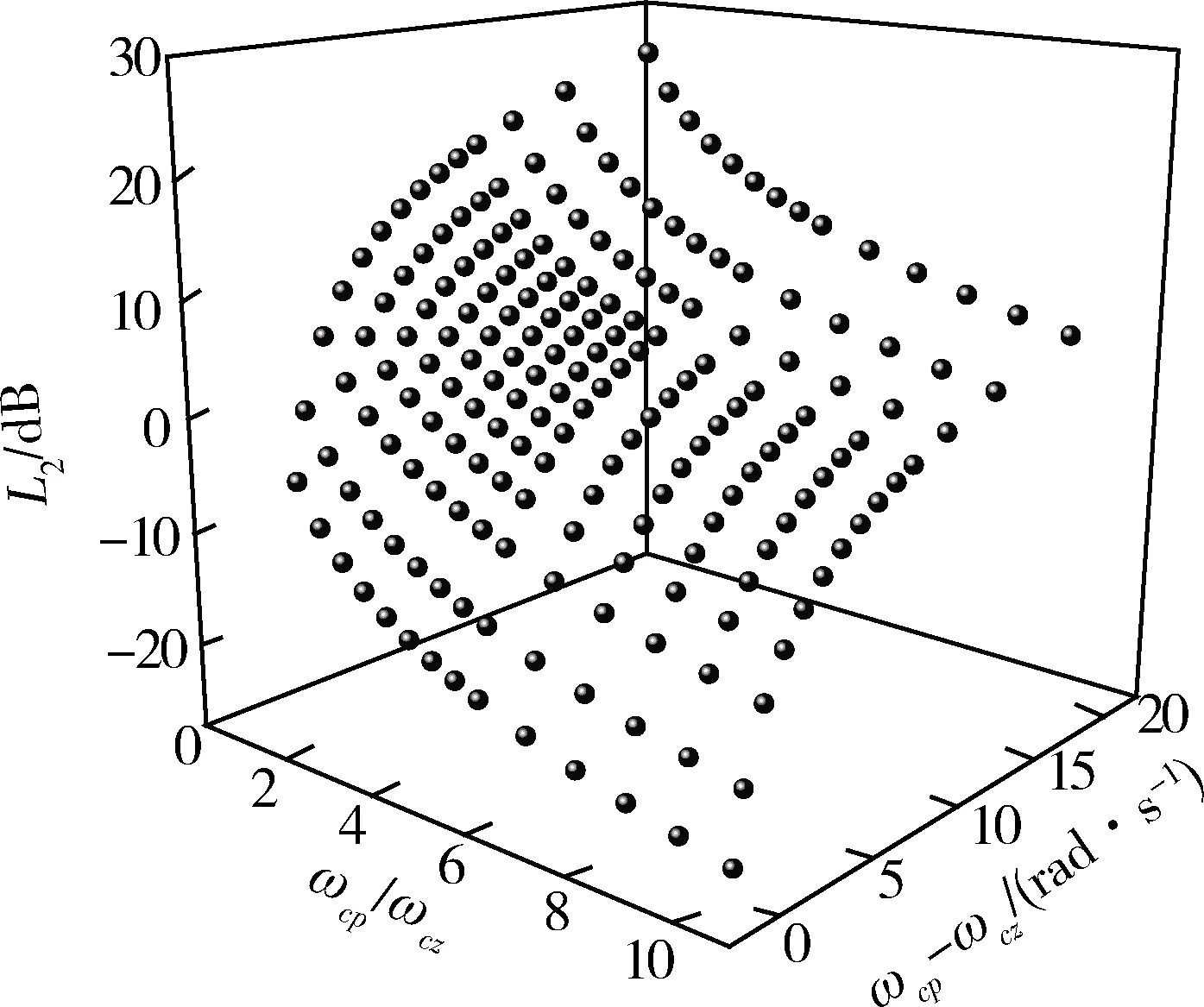
图1 控制参数ωcp和ωcz与幅值裕度映射关系
3 控制参数与幅值裕度的映射关系
3.1 基于代数方程求解的相位裕度计算
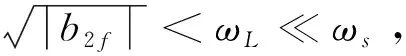
(13)

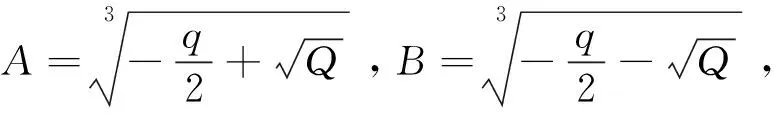
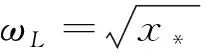
3.2 基于区间近似的相位裕度计算
根据前面的讨论,虽然俯仰通道姿态控制系统的相位裕度可以通过求解三次代数方程得到,但是计算结果与模型参数b2f和b3f存在复杂的非线性关系,无法类似于幅值裕度情形,进一步直接建立控制参数与相位裕度的映射关系。
下面根据俯仰通道姿态控制回路开环传递函数G(s)的对数相频特性函数的特点,通过迭代逐步缩小包含频率点ωL的区间。在完成若干次迭代之后,将θ(G)-(-π)在区间端点处的值作为相位裕度值,进而得到简化的相位裕度计算公式,并建立不含模型参数的控制参数与相位裕度的映射关系。
为了保证姿态控制系统稳定,选取的控制参数kc需要满足kc>-b2f/b3f[13],即有b3f·kc+b2f>0。因此可以定义数列{ω1,n}:
(14)
和数列{ω2,n}:
(15)
在式(14)和式(15)中,函数f(x)定义为:
(16)
显然,该函数在区间[0,+∞)内严格单调递增。
注意到,b3f和kc均为正数,因此有
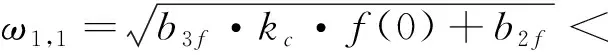
(17)
式(17)表明,数列{ω1,n}单调递增。
同理,由

(18)
可知,数列{ω2,n}单调递减。
因此,由式(13),或者等价的下式
(19)
可知,数列{ω1,n}和数列{ω2,n}均收敛,并且均收敛于ωL。令
(20)
显然有,
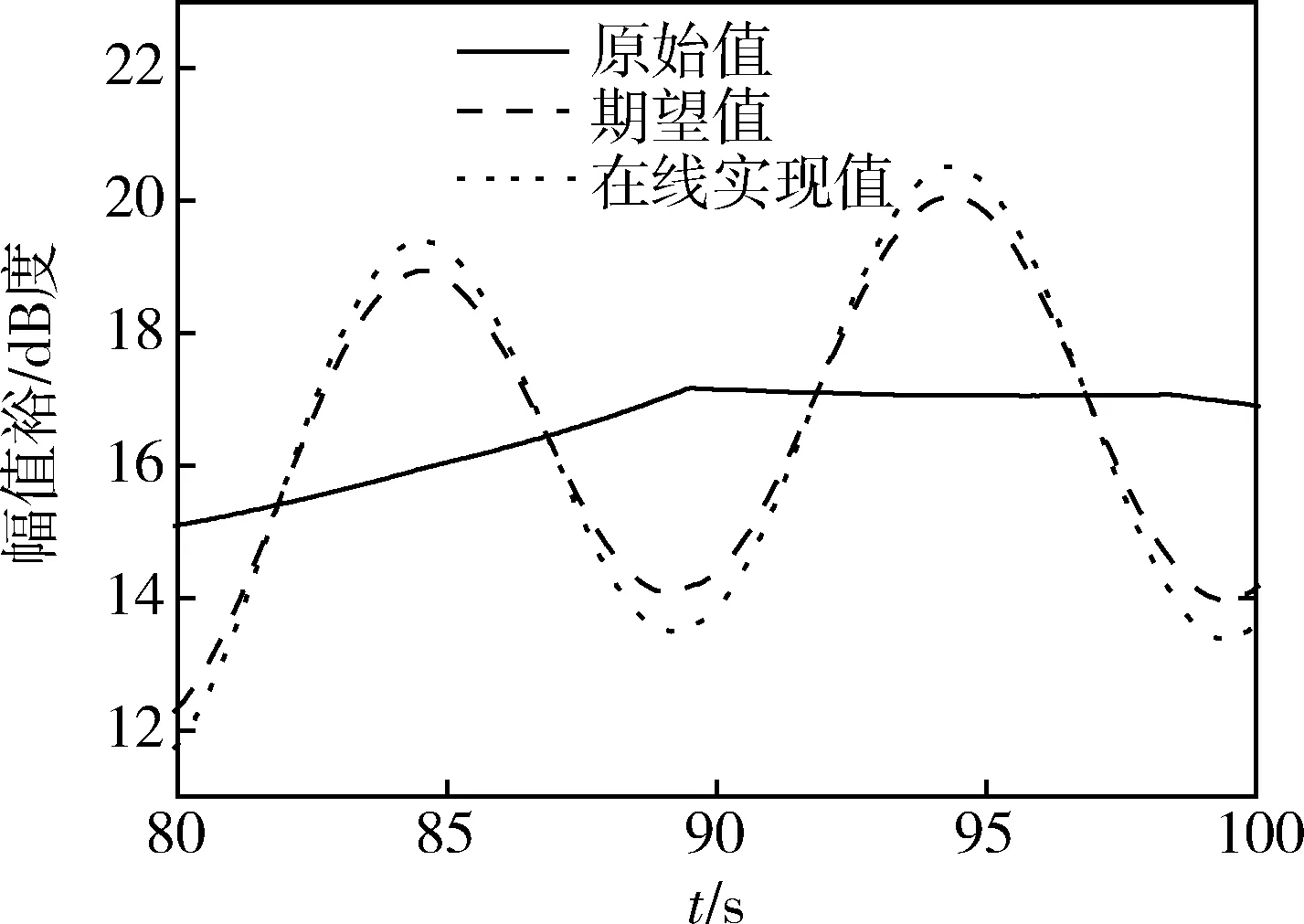
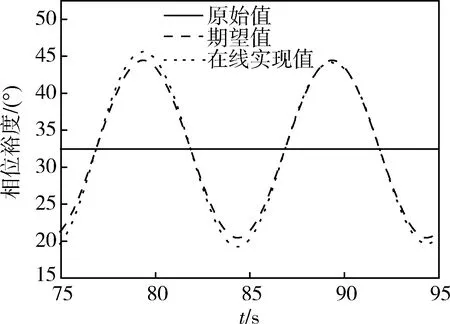
-∞ (21) 对于n=1,2,…,N,如果在设计控制参数时让kc满足 (22) 那么,根据式(17)~(22)式可得 [ωcpx1ωcz1-x1,ωcp1-x1ωczx1]⊂ (23) 并且, ωL∈[ωcpxNωcz1-xN,ωcp1-xNωczxN] (24) 另外一方面,注意到∀x∈(-∞,1/2],控制器相频特性曲线满足 (25) (26) 因此,在代入θ(G(jωL))-(-π)近似计算俯仰通道相位裕度时,可以用ωcpxNωcz1-xN或者ωcp1-xNωczxN替代ωL,即当条件(22)满足时,俯仰通道姿态控制系统相位裕度可近似为 (27) 将式(27)“≈”号右边的两项分别记为 (28) 和 (29) 显然有θ1(ωcp,ωcz)≫θ2(ωcp,ωcz,ξs),即θ2(ωcp,ωcz,ξs)相对于θ1(ωcp,ωcz)为小量。而θ1(ωcp,ωcz)仅与控制参数ωcz和ωcp相关,因此根据θ1(ωcp,ωcz)就可以得到控制参数ωcp和ωcz变化时,对应的θ(G(jωL))-(-π)的变化量,即分别建立了控制参数ωcp和ωcz与相位裕度之间的一种映射关系。从式(28)可以看出,相位裕度关于ωcz单调递减,关于ωcp则单调递增。 作为例子,当取xN=0.18时,分别以控制参数ωcp和ωcz为x轴和y轴,可以得到θ1(ωcp,ωcz)随控制参数ωcp和ωcz变化的曲面如图2所示。 图2 控制参数ωcp和ωcz与相位裕度映射关系 在基于控制参数与幅值裕度映射关系式(10)确定与期望的幅值裕度变化量对应的控制参数kc的变化量时,可以通过下面三阶泰勒展式计算得到控制参数kc的相对变化量, (30) 式中:ΔL为期望的幅值裕度变化量。 在基于控制参数与幅值裕度映射关系式(11),或者基于控制参数与相位裕度映射关系式(28),确定与期望的幅值裕度或者相位裕度变化量对应的控制参数ωcz和ωcp的变化量时,则可以采用两分法、割线法、牛顿法等迭代方法。 以某火箭为背景进行仿真验证时,在某偏差状态下飞行的80s~100s,期望的幅值裕度按幅值为3dB、频率为0.1Hz的正弦规律进行变化。通过对控制参数kc的在线调节,幅值裕度调节实现的效果如图3所示,从图可以看出,较好地实现了期望的幅值裕度变化规律。 图3 某偏差状态下幅值裕度在线调节效果 某偏差状态下,在火箭飞行的75s~95s,期望的相位裕度按幅值为12°、频率为0.1Hz的正弦规律进行变化。通过对控制参数ωcp的在线调节,相位裕度调节实现的效果如图4所示,从图可以看出,较好地实现了期望的相位裕度变化规律。 图4 某偏差状态下相位裕度在线调节效果 采用解析方式,建立了固体导弹(火箭)姿态控制参数与稳定裕度之间的映射关系,该映射关系可应用于姿态控制系统在线调节裕度,并通过数学仿真验证了映射关系的有效性。 考虑到在建立解析映射关系的过程中采取了一些近似处理,后续可以通过深入研究,提高映射关系的精度,同时将映射关系的适用范围推广到考虑弹(箭)体弹性影响的更广泛情形。此外,还可通过进一步的研究,与各类稳定裕度在线辨识方法相结合,实现稳定裕度调节回路的闭环。
[ωcpx2ωcz1-x2,ωcp1-x2ωczx2]⊂
⋮
[ωcpxNωcz1-xN,ωcp1-xNωczxN]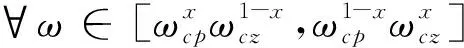
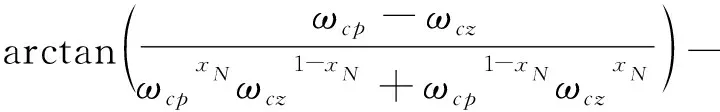
3.3 控制参数与相位裕度映射公式
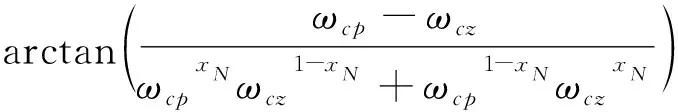

4 应用算例与数学仿真

5 结论
