高中数学课堂培养学生的思辨意识提升学习能力
2020-09-03王荣
王 荣
(四川省德昌中学 四川 凉山 615500)
1.勤于观察,三思而行,找到解答问题的突破口
在人类认识事物的过程中,感觉和知觉是最简单的认识方式,而观察作为知觉的最高状态,对于认识事物有着至关重要的作用。观察活动是一种主观能动性的发挥,具有一定的计划性、目的性和思维性。观察的过程也是认识问题,分析问题和酝酿方法解决问题的过程。在高中数学试题中,都有一定的已知条件和未知条件,要想解决问题,把握试题中的层层关系,就必须要仔细的观察,然后依据数学常识,开展探究和思考,通过现象发现本质,确定问题的解决思路和方法。

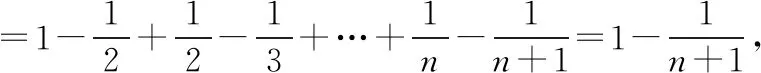
观察虽然只是解决问题的一种思维方式,只能发现问题的表象,但这为分析问题和解决问题提供了线索,为发现规律提供了信息。观察过程中,可以依据题目的具体情况采取常见的解题方法或者特殊的解决策略。
经典案例:3x2+2y2=6x,求x2+y2的最大值。

【解题过程】
由3x2+2y2=6x得

∴当x=2时,
x2+y2有最大值,

2.巧用联想,善于思考,拓宽解题思路
数学问题具有一定的逻辑性和关联性,在解决这些问题的时候必须具备一定的知识体系和联想能力。联想是组建知识体系,转化数学问题的过程,它可以有效的打开问题的突破口,嫁接有关知识,实现灵活解答。

通过给出的方程组可以看出,反应的是两个数的和与差的问题,结合所学的数学知识可以联想到韦达定理,x、y是一元二次方程t2-2t-3=0 的两个根,这样问题就迎刃而解了,答案是-1和3或者3和-1.
例4:a、b、c均为正实数,并且a2+b2=c2,n为不小于3的自然数,求证:an+bn 【解题分析】 从给出的已知条件a2+b2=c2可以运用联想,把问题想象为直角三角形的问题,求证的问题就可以转化为三角函数的问题。 【解题过程】 从已给条件可以转化问题,得知C是直角,A为锐角 当n≥3时,有sinnA 于是有sinnA+cosnA 从而就有an+bn 数学问题的出现往往是伴随着所中问法和多种解决方法的,其实数学解题是命题的连续变换。对于一些数学难题,可以活学活用,拓展解题的思维,转化问题。在转化的过程中,要由繁到简,由抽象到具体、有未知到已知,往往问题的转化是经过上述的观察和联想之后出现的。 求证a、b、c三数中必有两个互为相反数。通过以往学习的数学知识,并仔细观察可以把问题转化为(a+b)(b+c)(c+a)=0,这样问题就不攻自破了。 【解题分析】对于给出的求证问题来说,没有固定的形式或者说是数学式子,这一定成都上加大了解题的难度,直接求证的话根本找不到突破口。那我们就从问题出发,把问题转化为a-1、b-1、c-1中至少有一个为零,这样问题就显得完整易解答了。 【解题过程】 于是 (a-1)(b-1)(c-1)=abc-(ab+ac+bc-1)+(a+b+c) =0. ∴a-1、b-1、c-1中至少有一个为零,即a、b、c中至少有一个为1。 要想又好又准又快的解决数学问题,再依赖传统的分析综合等方法已经不再可能实现。从近些年数学问题的考察内容和形式来分析,要想解决数学难题,必须要学会思维的变通,所谓“变则通,通则达”。思变就是依据提升给出的条件,并结合学习的相关知识,提出灵活简便的解题方案,主要的方法有观察法、联想法和转化法等。目前,高中数学试题考察的内容和形式都发生了一定的变化,具有极强的灵活性、探究性和逆向思维性。为了更好的解决数学难题,学生必须在掌握基础数学知识的同时,熟悉一般的数学解题方法,并且要做到思变,学会变通,切勿死板。
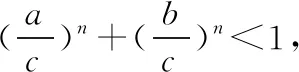
3.学以致用,学会转化,换个思路解答问题