主井深度爆破对周边建筑物的影响*

马谕杰,唐海,2*,万文,朱帅帅,丁安松,王建龙

(1.湖南科技大学 资源环境与安全工程学院,湖南 湘潭 411201; 2.湖南科技大学 煤矿安全开采技术湖南省重点实验室,湖南 湘潭 411201)

爆破开挖地质条件适应性强,开挖成本低[1],在矿山井巷的施工中已得到了广泛应用.但爆破施工会产生爆破振动,对周边环境要求较高,若爆源周边存在建筑物,则由爆破产生的振动会引起周边建筑物的振动,导致建筑物产生裂缝,对以后的使用埋下安全隐患[2].为探究爆破振动对周边建筑物的影响,许多学者以爆破振动对周边建筑物的安全影响为前提,开展了关于降低爆破振动速度方法的研究.常方强[3]研究了城市立交桥爆破对周边建筑环境的影响,提出开挖减震沟,增加减震沟深度等减小振动的方法.姜增国[4]为确保建筑物的稳定性,利用孔内、孔间微差去减小爆破振动.张梦雅[5]提出在建筑物周边进行爆破时需要控制最大单响药量,以及进行长期爆破时需考虑建筑物的累积损伤效应.Tian X X[6]分析了在隧道爆破施工中周边建筑物的振动频率与振动速度,认为应对爆破影响区域进行分区处理,并提出了隧道分区爆破减振方案.

目前,采用振动监测仪监测振动速度和数值模拟的方法,研究工程爆破对周边建筑物影响的成果较多[7-12],但在考虑振动高程放大效应的前提下,其周边建筑物的安全与稳定的研究还相对较少.为确保某大型磷矿主井爆破过程中周边建筑物的安全与稳定,作者考虑了振动高程放大效应,运用数值模拟和理论计算相结合的方法,对主井爆破时周边建筑物的稳定性进行了研究.

1 工程背景

瓮福磷矿位于贵州瓮安福泉境内.地理坐标:东经107°20′～107°26′,北纬26°55′～27°05′.矿区南北长17.5 km,东西宽2.25～4.00 km,面积为58 km2.现阶段瓮福磷矿采用露天开采,服务年限26 a,之后将全部转为地下开采,其露天开采现状见图1.在进行地下开采准备时,需要爆破开挖主井,但主井周边存在建筑物,且建筑物与主井距离较近,在爆破之前需对建筑物进行稳定性研究.根据现场勘探资料可得,建筑物中破碎站距主井最近且距离仅为30 m,主井爆破作业对破碎站影响较大,故选取破碎站进行稳定性研究.其余建筑物结构和破碎站相同(均为钢结构厂房),在爆破过程中若能保证破碎站安全,其余建筑物必然也安全.主井与破碎站位置示意图见图2.

图1 露天开挖现状

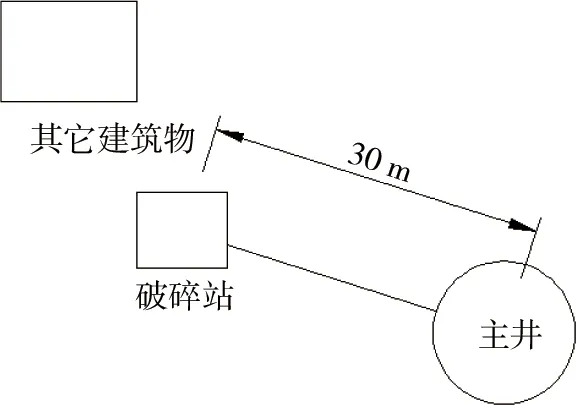
图2 主井与破碎站位置

2 爆破设计方案

原爆破设计方案在主井每次爆破中设置掏槽眼13个,辅助眼26个,周边眼32个,采用直眼掏槽,掏槽眼深4.7 m,孔径为50 mm,其他炮眼深4.5 m,孔径为40 mm.主井爆破参数见表1,爆破炮眼布置及主井掘进示意图见图3.

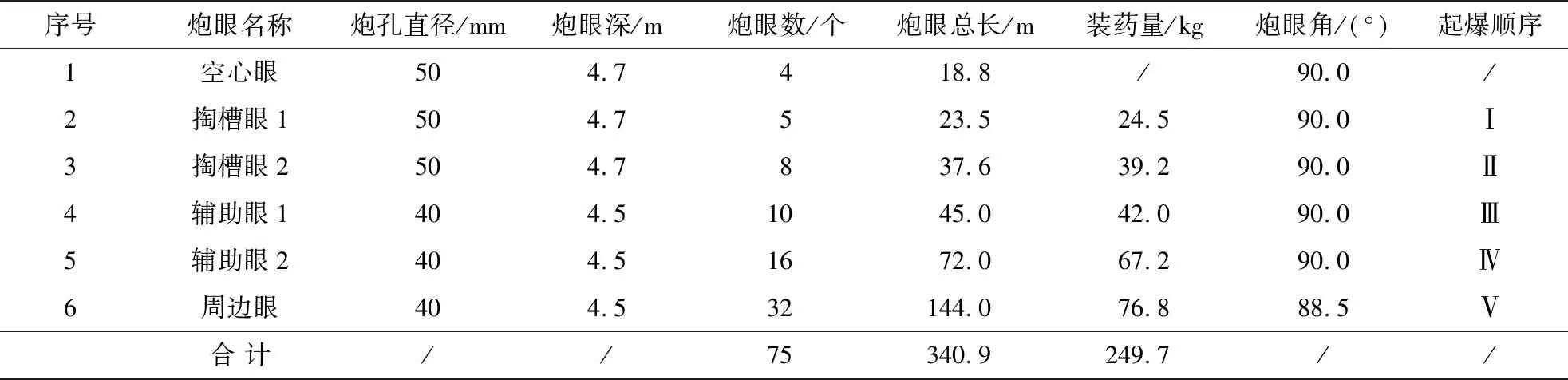
表1 主井爆破参数表

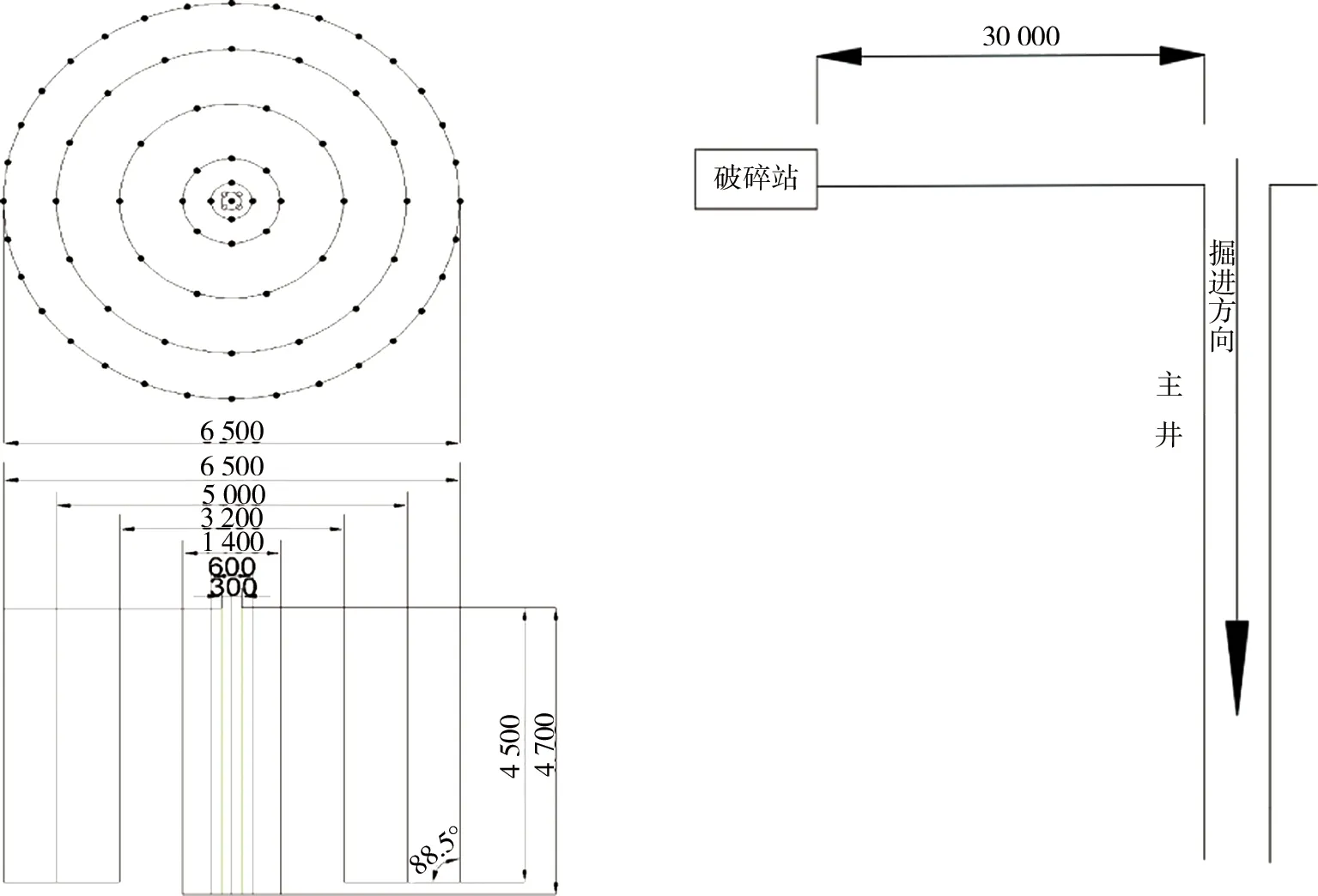
图3 主井爆破炮眼布置与开挖掘进(单位：mm)

3 有限元数值计算模型

利用数值模拟软件ANSYS+LS-DYNA对主井爆破掘进过程中破碎站的振动速度进行分析,以便对主井掘进爆破过程中破碎站的振动规律及动态响应有更全面的认识和判断.

3.1 模型建立

根据原爆破设计方案进行数值模拟,假设岩体是均质、连续、各向同性材料.在这种情况下,岩石将采用MAT_PLASTIC_KINEMATIC材料模型,该模型以Cowper-Symonds关系式为基础来考虑应变率的影响,适用于包含应变率效应的各向同性材料,可用来模拟爆破荷载下的岩石.炸药采用LS-DYNA中炸药特属的高能炸药材料模型,相关材料模型为MAT_HIGH_EXPLOSIVE_BURN,爆炸采用JWL状态方程.主井岩层主要为白云岩,其动态力学参数见表2,炸药及JWL状态方程参数见表3.

表2 白云岩动态力学参数

表3 炸药参数

空气采用MAT_NULL空气材料模型,结合状态方程*EOS_LINEAR_POLYNOMIAL描述空气的作用.其相关材料参数见表4.

表4 空气材料参数

3.2 计算分析模型

3.2.1 模型建立

在爆炸的模拟中,常常会出现单元网格严重畸变而导致数值计算终止的问题,采用ALE/Euler算法可以克服此问题,从而实现流体固体耦合的动态分析.本模型中对炸药、 空气采用 ALE 单元,对岩体采用Lagrange单元,通过*CONSTRAINED_LAGRANGE_IN_SOLID关键字进行耦合.单元类型选用3D solid164.根据主井掘进深度的增加,不断改变炸药的位置,以及主井中空气层的高度.

3.2.2 边界条件

空气模型四周定义为无反射边界,前后面约束其相应位移,岩石上部定义为与空气接触面即自由面,左右面约束其对应位移,下边固定.设计炸药位置为主井爆破爆源,根据工况中的破碎站与主井位置,设置监测点,监测点距主井爆破爆源水平距离30 m.

根据原爆破设计方案,最大段装药量为79.8 kg,本次模拟装药量均设置为80 kg,模拟主井按原设计方案爆破对破碎站的影响.模型示意图见图4.

图4 数值模型计算

3.3 模拟结果及分析

模型求解之后,运用LS-DYNA后处理软件测出不同掘进深度时监测点的振动速度.主井掘进深度分别为4,36 m时,数值模型的应力云图见图5.

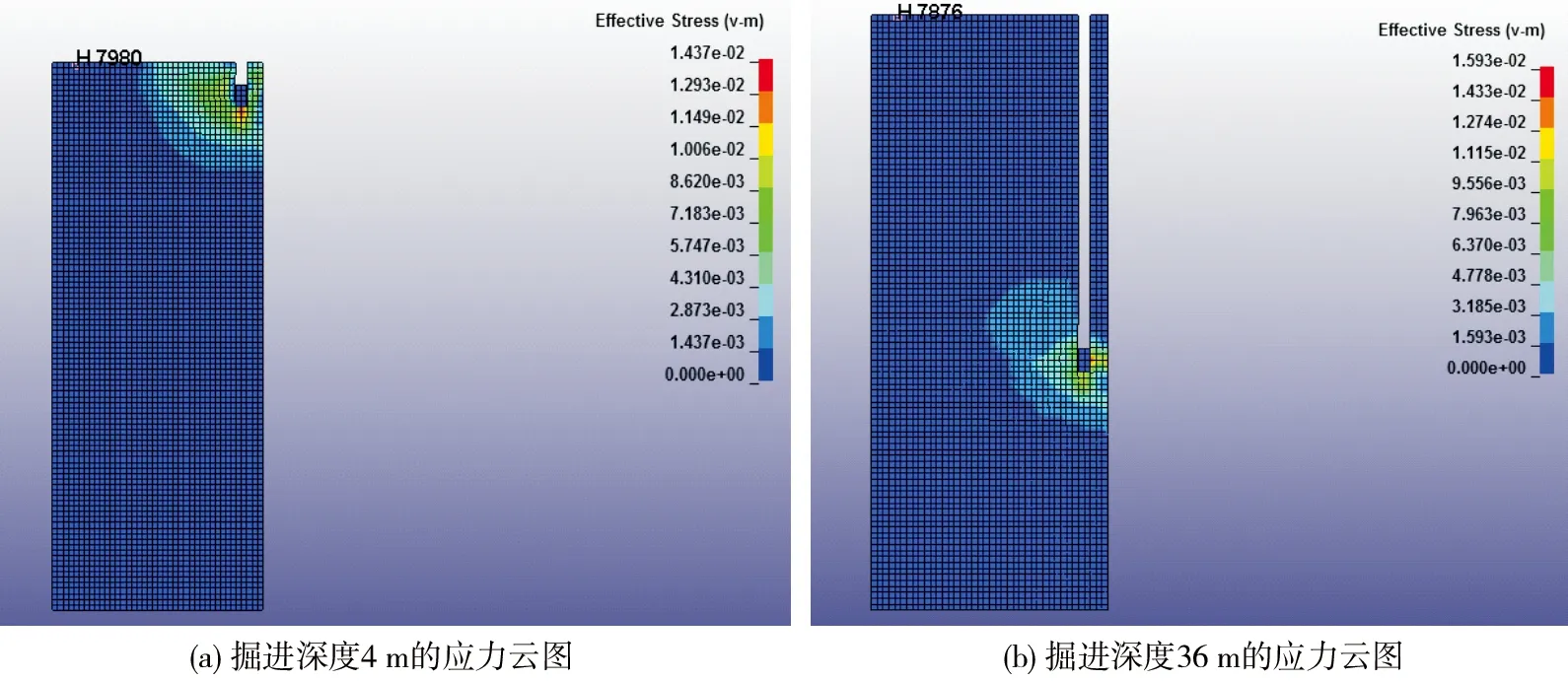
图5 不同爆破深度时模型的应力云图

监测点高程是相对爆源来说的,在数值上等于主井深度.随主井掘进深度不同,爆源距及监测点高程均发生变化,提取模拟结果中监测点振动的峰值速度将其列于表5中,爆破深度与振动速度峰值的关系见图6所示.

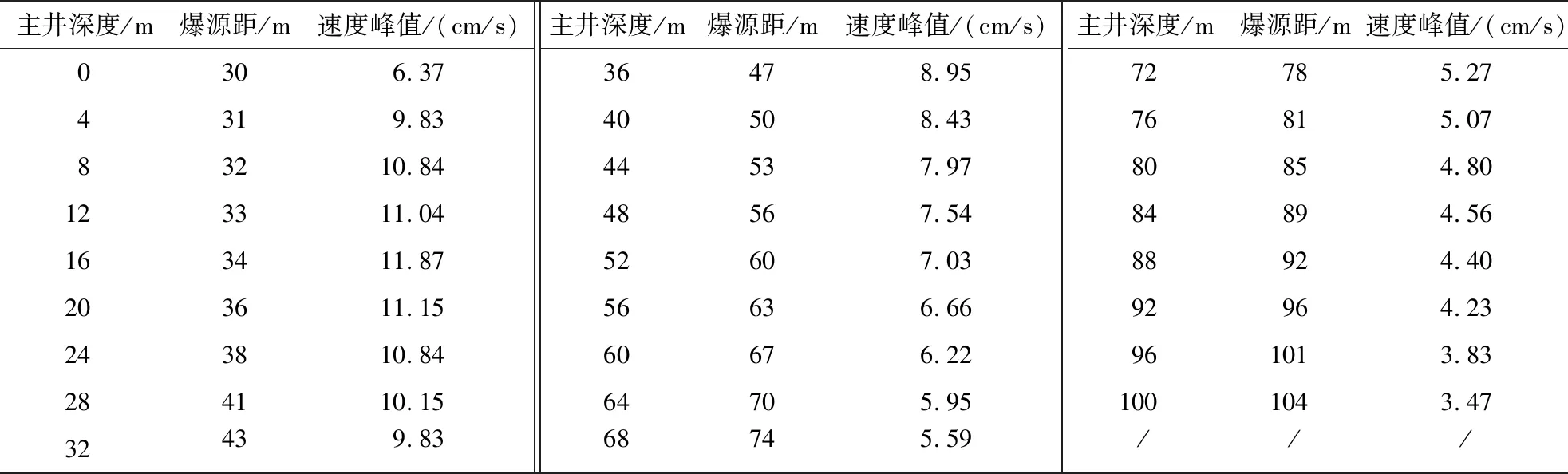
表5 不同爆破深度时监测点振动速度峰值

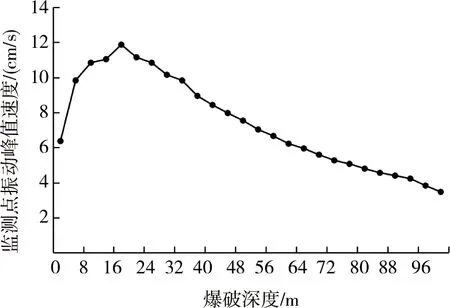
图6 模型爆破深度与速度峰值的关系

4 理论基础与计算

4.1 理论基础

采用爆破发生时建筑物的振动速度作为评价建筑物是否安全的标准已被国内外所认可.爆破振动主要与一次爆破中的最大段药量有关,在实际的工程爆破中,通常根据炸药的单耗和每次爆破的土石方量去确定一次爆破所需的炸药量,而后根据式(1)预测周围建筑物的振动速度.

(1)

表6 爆区不同岩性的K,α值

式中:V为被保护对象允许的振动速度,cm/s;Q为一次起爆最大段药量,kg;R为被保护对象至爆源中心的距离,即爆源距,m;K,α分别为爆破振动波衰减系数与衰减指数,其取值范围见表6.

主井爆破掘进的过程中,破碎站与爆源之间存在着高程差.许多学者研究了由高程差导致的爆破振动高程放大效应[13-21],并根据现场监测结果回归分析得到了考虑高程放大效应的质点振动速度计算公式.

文献[13,14]研究了高边坡的放大效应,认为放大效应并不是随坡高单调增加,还与爆源距、岩性有关.并由现场振动监测实例回归分析得到了质点的振动速度公式:

(2)

式中:H为测点与爆心之间的相对高差,m;β为高差影响系数.

周同岭[15,16]认为测点与爆源之间的相对高差对振动有很大的影响,给出高差为正时振动增大；高差为负时振动降低的结论.并指出质点的振动速度公式应由式(3)决定.

(3)

式中:β取0.25～0.28,正高差时取正,负高差时取负.硬岩中取大值，软岩中取小值.

也有学者[17]在萨道夫斯基的公式基础上,增加了高程影响因子,将质点振动速度公式修改为

(4)

式中:S为爆心到测点的水平距离,m.

唐海等人[18-20]通过量纲分析也得到了反映高程放大效应的爆破振动速度计算公式

(5)

式中:K1为平整地形的场地系数;K2为边坡等凸形地貌影响系数;β1为衰减系数;β2为高程差影响系数.

由目前的研究成果可知,测点与爆源之间存在的高程差会引起振动的高程放大效应.故在进行破碎站的稳定性分析时应考虑高程产生的影响.

4.2 高程放大公式的选取

纵观以上提到能反映高程放大效应并预测爆破振动速度的公式不难发现,式(2),式(4),式(5)都是需要根据现场爆破情况进行监测,并根据监测结果进行回归分析来确定高程影响系数,即在存在高程差的情况下爆破已经发生.若已知爆源与测点之间存在高程差,还未进行爆破的情况下,需对测点的振动速度进行预测,不难发现这些公式并不适用,而且其系数较多使用起来并不方便.因此,在这种情况下,选用式(3)较为合适.对式(3)进行变换得到式(6).由式(6)便可计算得到考虑高程放大效应下的最大段药量.

(6)

4.3 理论计算

4.3.1 原爆破设计方案

表7 小炮实验振动监测结果

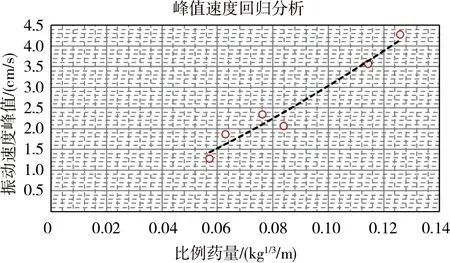
图7 监测结果回归分析

由此便得到平坦地形下爆破振动峰值速度衰减规律:

(7)

参照表1,取其第一次爆破最大段装药量76.8 kg代入式(7),计算得到主井第一次爆破时破碎站振动速度为8.85 cm/s,根据文献[22]得到建筑物爆破振动安全允许标准,见表8.

表8 爆破振动安全允许标准

根据小炮实验的监测结果,破碎站应采用工业和商用建筑物振动速度阈值,参照表8,其值取4.2 cm/s.由于8.85 >4.2,故在不考虑高程影响下的第一次平坦地形的爆破中,破碎站的振动速度超过了阈值4.2 cm/s,即破碎站不安全.

而由数值模拟的结果可知,随着主井的爆破深度不断增大,监测点的振动速度出现先增大后减小的趋势.由此来分析,当按照原爆破设计方案进行主井掘进爆破时,破碎站的振动速度会先增大后降低.

4.3.2 考虑高程放大效应

考虑高程放大效应对原爆破设计方案进行优化计算,通过控制其最大段装药量来确保破碎站的安全.主井第一次爆破对破碎站无高程差的影响,取破碎站振动速度阈值4.2 cm/s,将数据代入式(7).主井第二次爆破及后续爆破中爆源与破碎站以每次循环约4 m高程差逐渐加大,存在高程差的影响,将数据代入式(6),白云岩属于硬岩取β=0.27,得到当主井掘进至约76 m时,爆源距为81 m,最大段药量为82.1 kg.主井爆破掘进前92 m最大段装药量详见表9,其线性关系见图8.从表9和图8可看出,为保证破碎站振动速度不超过安全阈值,主井掘进爆破的最大段装药量随掘进深度增加有先减少后增加的趋势.

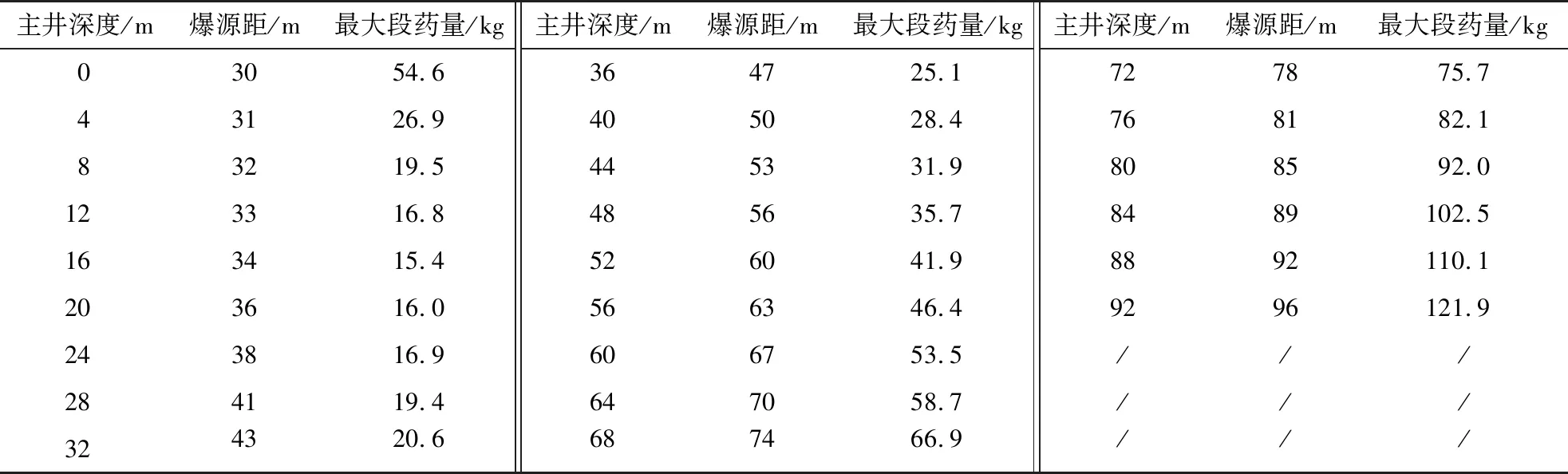
表9 主井爆破最大段装药量

图8 主井深度与最大段药量的关系

5 结论

1)随着主井爆破掘进深度的不断增加,爆破中爆源与破碎站的高程差也在增大,破碎站受到高程放大效应的影响,其振动速度出现先增大后减小的规律.

2)为保证破碎站在爆破过程中的安全,在考虑高程放大效应的前提下,最大装药量应随着主井深度先减少后增加.

3)按照原设计方案进行施工时,主井掘进深度为0～72 m时破碎站振动速度峰值均超过阈值速度,影响破碎站稳定,需要控制最大段药量;主井掘进深度超过72 m时破碎站振动速度峰值未超过阈值速度,此时主井爆破掘进可按原设计方案进行.