锚杆锚固力无损检测的数值模拟*

樊智,苗晓伟,李青锋,谷洪飞,张建业

(1.潞宁煤业有限责任公司,山西 忻州 036700;2.湖南科技大学 资源环境与安全工程学院,湖南 湘潭 411201)

锚杆支护技术在地下空间、矿山、隧道等相关领域得到了高效的应用.随着锚杆支护技术的不断发展和广泛应用,锚杆支护质量的检测也越来越受到科研人员的重视[1].现阶段,锚杆支护质量检测手段主要有2种,一种是检测结束后锚杆锚固状态被破坏的有损检测,另一种是对锚固系统没有破坏的无损检测.工业现场仍以有损检测为主要检测手段,无损检测技术未得到普及[2].科研工作者在无损检测锚杆长度方面取得了一定的成果,推动了无损检测的发展,但是,对于锚杆锚固力无损检测的研究很少[3].在工业现场实践中,锚杆锚固力是评价锚杆锚固质量的关键因素[4],因此,对于锚杆锚固力的研究尤为重要.本文在前人[5]研究基础上,运用FLAC3D数值模拟软件对预应力锚固体锚杆外露端面施加不同的工作荷载,研究不同工作荷载对锚杆锚固力的影响,同时进一步探究锚杆锚固力求解的方法.

1 锚杆锚固力无损检测理论分析

不少学者[5,6]认为,影响锚杆锚固段剪应力的主要因素有2个方面:一方面,围岩的硬度对锚杆在锚固段所受剪应力有影响.随着围岩硬度增大,锚杆受到剪应力越集中,且峰值剪应力值也就越大;随着围岩硬度减小,锚杆受到剪应力的分布范围会分散扩大,峰值剪应力值也就越小;另一方面,锚固体直径对锚杆所受剪应力有影响.随着锚固体直径增大,锚固段锚杆受到剪应力减小,锚杆受到剪应力的分布范围会分散扩大.文献[7]认为锚杆锚固段的初始剪应力峰值大小与后移的锚固段峰值大小是相等的,且峰值点和零值点的距离为常数.文献[8]通过锚固锚杆的静载加载试验和锚固锚杆实际受到荷载情况下的荷载分布规律,通过微元法建立一个关于锚固锚杆的力学方程,求解力学方程可知锚固锚杆杆体表面的剪应力呈现指数函数分布.文献[5,9,10]通过总结前人成果得出,锚杆锚固段在达到最大锚固力时,锚杆锚固界面的剪应力分布曲线如图1所示,锚杆锚固界面的剪应力可以分为4个阶段,分别是摩擦区、塑性弱化区、塑性硬化区、弹性区,从图中可以看出,0～l1阶段为摩擦区,其剪应力值近似为τ0,且剪应力值趋于水平;l1～l2阶段为塑性弱化区,此阶段的剪应力在刚刚结束摩擦区的阶段后,曲线呈现线性增大;当剪应力值增大到峰值τ1后,剪应力呈现出l2～l3阶段,此阶段为塑性硬化区,该段剪应力在达到峰值后的变化呈指数分布状态且逐渐减小;减少至l3以后的阶段为弹性区,该段剪应力继续以指数分布减小,及至无限接近于零剪应力状态.其中,在指数分布区段的指数函数为

(1)

式中:τ1为锚固界面最大剪应力;D为锚固孔直径;K为粘结界面剪切刚度;E为锚固体弹性模量;B为锚固剂厚度;x为锚固段上某一坐标到锚固起始位置的距离.

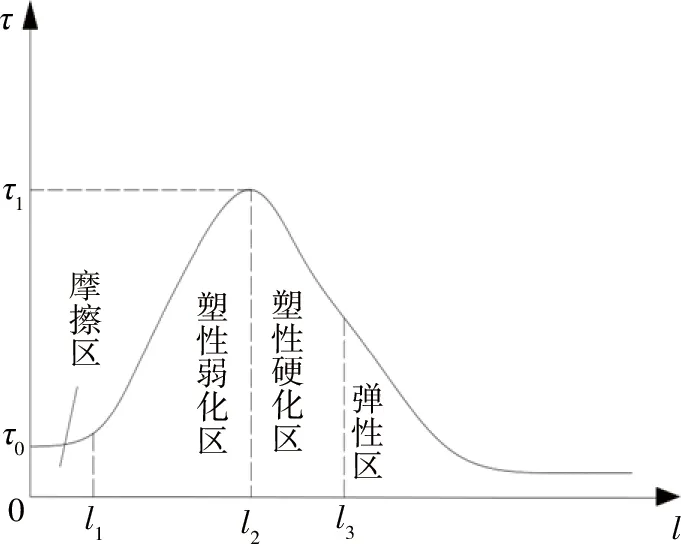
图1 锚固段粘结界面剪应力分布

令锚杆锚固段锚固界面发生完全脱粘时的位移为u0(即l1),从锚杆锚固界面开始脱粘(对应于锚固界面剪应力为τ1)到锚杆锚固界面完全脱粘(对应于锚固界面剪应力为τ0)的锚固段长度为l0(即l0=l2-l1),由锚杆锚固界面开始脱粘(此时锚杆锚固界面剪切刚度为K)到锚杆锚固界面完全脱粘(此处锚杆锚固界面剪切刚度近似为0)段的平均剪切刚度为0.5K,则锚杆锚固段峰值前半区段的应力面积即在l0长度区段内的应力面积为

0.5(τ1+τ0)l0=0.5Ku0.

(2)

式中:l0为起始脱粘时到完全脱粘时的锚固段长度;τ0为锚固界面完全脱粘时的剪应力;u0为锚固界面完全脱粘时的位移.

令锚固段长度为la,则峰值后半部分的应力面积为

(3)

式中:la为锚固段长度.

综合式(1)～式(3)推导可得锚固段锚固力为

(4)

由前述文献[6,7,10 ]和式(4)分析可知,在锚固孔直径、锚固剂材料、锚杆一定的条件下,式(4)中的参数D,u0,E,l0,la参数值不变,而K,τ0是影响锚杆锚固段锚固力的关键参数,其中τ0与锚杆锚固段的巷道围岩压力有关,K值可以通过应力波在锚固锚杆传播时,传播至锚杆锚固段末端的反射波能量得到.此外,由以上可知应力波在锚杆非锚固段以及自由锚杆传播时,应力波的振动速度值、传播位移只与应力波初始激发波的幅值有关,当应力波传播至波阻抗变化界面时才会发生反射现象,进而振动速度值、传播位移发生变化.

2 锚杆锚固力无损检测数值模拟

图2 锚固锚杆初始模型

数值模拟是一种利用计算机在现代数学和力学基础上进行科研求解的方法,它顺应当代计算机的迅猛发展,是在科学理论分析、实验室及工业现场实验研究之后的又一种重要的科研方法.本文采用FLAC3D数值模拟软件建模,FLAC3D为连续介质有限差分力学分析程序,它采用显式差分法求解微分方程,可以进行非线性动力反应分析,且具有强大的动力分析功能[11].

用FLAC3D数值软件建立初始模型[9,10,12],模型尺寸:围岩尺寸400 mm×600 mm×2 400 mm,锚杆直径20 mm,锚杆长度2 200 mm,锚固孔直径34 mm,孔深2 000 mm,锚固剂厚度7 mm,锚固长度1 000 mm.由于模型求解时间受网格尺寸的影响很大,考虑到计算机内存、计算时间等因素,经过多次网格的划分求解,结合计算精度和计算速度,最终所建模型单元体个数为37 120个.在动力分析部分,为了减少波在边界上的反射,模型边界条件选取无反射边界条件,如图2所示.

表1 模型中岩石力学参数

2.1 不同工作荷载下应力波在锚杆中传播特性的时域分析

为了研究工作荷载对应力波在锚杆中的传播特性,在锚杆锚固长度、激振首波不变的前提下,建立了工作荷载为0.00, 0.30, 0.35 GPa,分别在激振点、锚固起始端、底端采集应力波在锚杆中的传播数据,应力波传播如图3～图5所示.

由图3可以看出,应力波在传播至锚杆锚固起始端时为波阻抗变化界面,由激振点检测可以明显看到波阻抗界面波峰,传播过程中应力波首波过后应力波衰减明显,在第二轮传播结束后,波峰衰减幅值非常大;在锚固起始端采集的波形表明,应力波在底端反射波峰急剧衰减,第一轮传播结束后,第二轮传播锚固起始端波阻抗变化界面的波峰已经非常微小了,锚杆底端反射就更微小了,由此,在分析波形传播特性时,波形的第一轮传播最为关键.

对比图3与图4可知,施加0.30 GPa工作荷载后,激振点处采集的波形与未施加工作荷载的波形差别较小,其中锚杆锚固起始端的波峰有轻微的减弱;在锚固起始端采集的波形在应力波传播至锚固起始端后波形幅值整体增大;在锚杆底端采集的波形在应力波传播至底端后,应力波快速抖动,传播至锚杆激振点附近抖动衰减;施加工作荷载后,应力波的传播轨迹变化较小.

对比图4与图5可知,在施加0.35 GPa的工作荷载后,锚杆内传播的波形在激振点、锚固起始端、锚杆底端采集的波形相比图4的波形差异不明显,施加工作荷载后,应力波的传播轨迹变化较小.

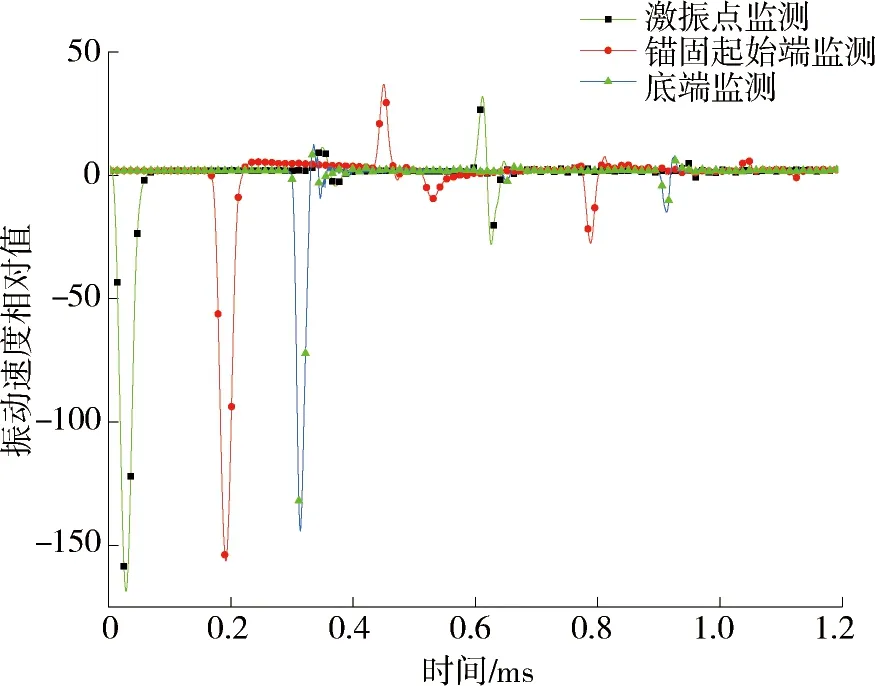
图3 工作荷载为0 GPa时应力波在锚杆中传播波形

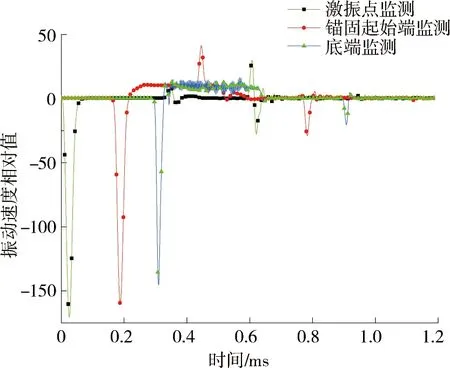
图4 工作荷载为0.30 GPa时应力波在锚杆中传播波形

图5 工作荷载为0.35 GPa时应力波在锚杆中传播波形

综合以上分析,锚固锚杆在施加工作荷载后,工作荷载对应力波存在影响,但存在的影响在时域图中并没有明显的差异,波形传播仍然主要受锚固质量和波阻抗变化界面的影响,本文数值模拟均在锚固参数相同的条件下施加不同工作荷载,因此,除工作荷载对应力波的影响外,其他因素不影响应力波的波形.

2.2 不同工作荷载下应力波在锚杆中传播特性的频域分析

通过FLAC3D模拟,得到不同工作荷载下应力波在锚杆中的传播波形图,对每一个时域波形进行快速傅里叶变换(FFT),得到在工作荷载分别为0.000,0.345,0.350,0.355,0.365,0.375 GPa的频域曲线,如图6所示.

由频域图得到每一个工作荷载的应力波主频,利用式(4)计算出锚固力值,主频与锚固力如表2所示.

由表2可知,在未施加工作荷载的锚杆锚固力为218.29 kN,此时锚杆锚固质量未受破坏,锚固力处于最大值;施加工作荷载为0.345 GPa后,锚固力减小至135.5 kN,锚杆锚固质量部分受到破坏;施加工作荷载为0.35 GPa后,锚固力继续减小至52.642 kN,此时锚杆锚固质量破坏非常严重,但仍具有部分锚固效果;施加工作荷载为0.355 ,0.365 GPa后,锚固力分别锐减到16.865,15.533 kN,锚杆锚固作用基本失效;施加工作荷载为0.375 GPa后,锚固力为0 kN,锚杆锚固作用完全失效;由以上锚固力失效过程可以看出,工作荷载的增大对锚杆锚固质量破坏越严重,在施加工作荷载后,可能存在一个阈值使得锚固力减小,阈值过后,锚固力便呈现下降趋势;在对锚杆施加预应力时,要十分精确地把握预应力的大小,以防止预应力过大而破坏锚固质量.

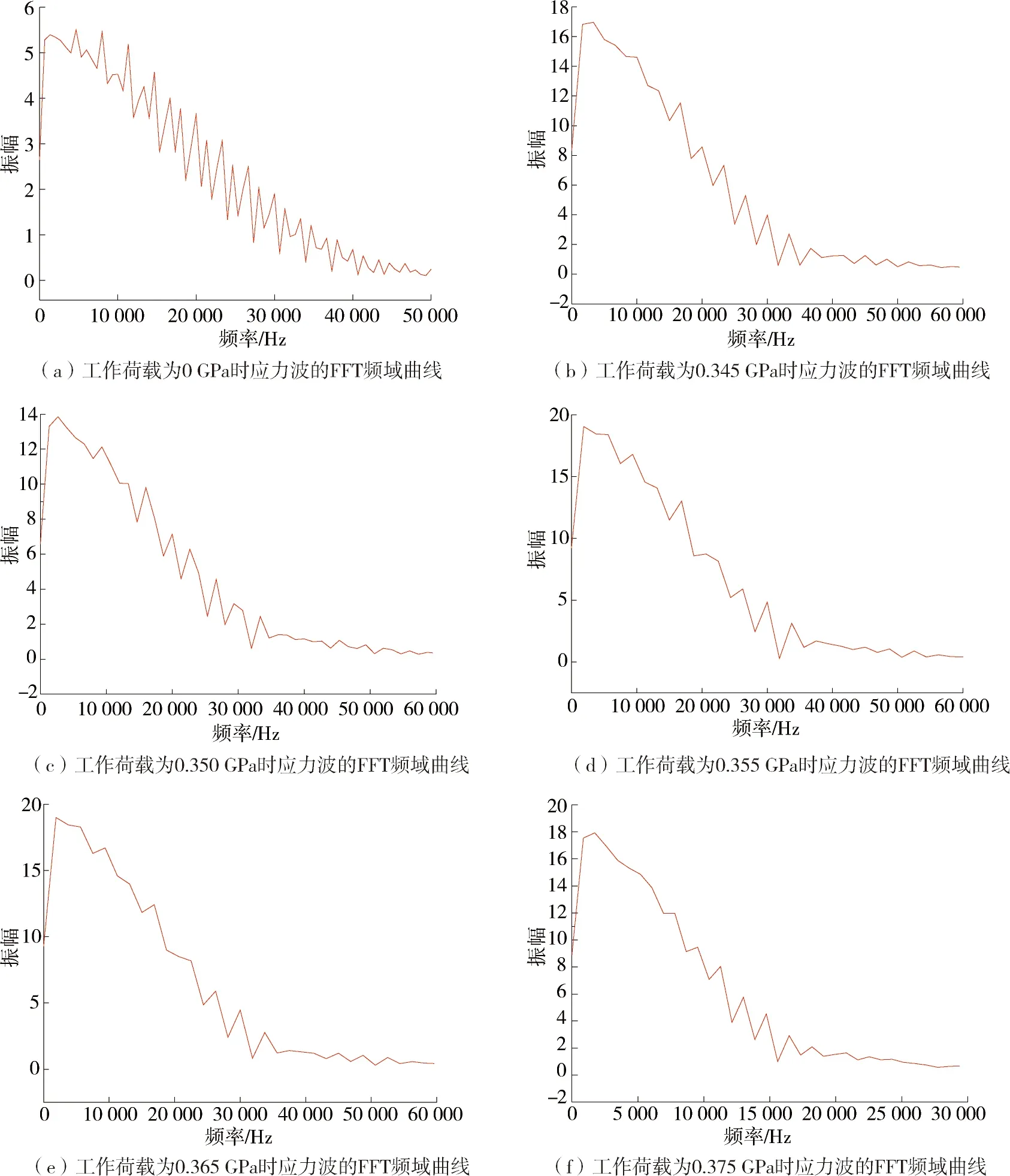
图6 不同工作荷载下应力波的FFT频域曲线

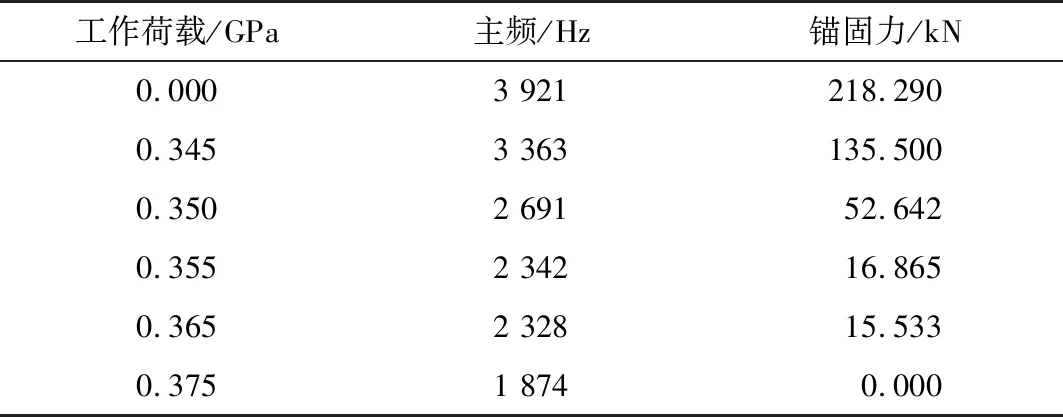
表2 不同工作荷载下主频和锚固力值

2.3 锚固工作荷载与锚杆拉出位移的关系分析

如图7,对模型的锚杆施加不同工作荷载,分别采集在不同工作荷载下模型中锚杆拉出的位移,得出应力-应变曲线如图8所示,施加工作荷载后锚杆产生3个阶段的位移轨迹,第一阶段为施加工作荷载在98.3～125.6 kN,此时,随着工作荷载的增大锚杆拉出位移缓慢增加,此时锚杆处于正常的服役状态,锚固状态未被破坏;第二阶段为施加工作荷载在125.6～118.4 kN,此阶段锚杆位移发生大幅度突变,锚杆锚固状态遭到破坏,锚固部分失效;第三阶段为施加工作荷载在118.4～52.5 kN,此阶段只能维持相对较小的工作荷载,但锚杆拉出位移增加相对很大,证明在第二阶段锚杆所能承受的最大工作载荷为125.6 kN,据此可推知锚杆的锚固力125.6 kN.

图7 不同工作荷载下锚固体位移云图

图8 不同工作荷载下锚杆相应的位移曲线

通过模拟得出应力波在锚固锚杆传播的时域曲线和频域曲线,并结合式(4)计算得到锚固力为218.3 kN,而通过不同工作荷载的数值模拟,得到的锚固力为125.6 kN,显然,两者之间存在一定的差异.但是,结合现场实际情况,在式(4)中考虑一定的比例系数,由实测波形的时-频特性计算锚固力是可行的.

3 结论

1)锚杆在施加预应力后对应力波在锚杆中传播波形是有影响的,预应力可以增大首波过后的应力波峰值,当峰值过大时,会影响锚固起始位置的识别.

2)对锚固锚杆进行拉拔试验均有一个峰值拉拔力,且在峰值拉拔力过后,锚固承载力迅速降低,锚杆锚固开始失效,此时可认为拉拔力峰值为锚固力;随着工作荷载的增大,锚杆锚固质量受损,锚固力降低,在对锚杆施加预应力时,要十分精确地把握预应力的大小,以防止预应力过大而破坏锚固质量.

3)锚固力关系式是可以作为判断锚杆锚固力大小的依据,结合现场实际情况,在锚固力关系式中考虑一定的比例系数,由实测波形的时-频特性计算锚固力是可行的.