基于帧重叠的变速跳频信号分选算法
2020-09-02蔡晓霞雷迎科
王 淼,蔡晓霞,雷迎科
(国防科技大学电子对抗学院,安徽 合肥 230037)
0 引言
盲源分离,作为信号分选的核心步骤,所要解决的问题是在不知道源信号和不对未知的混叠系统(接收阵列天线系统)参数做任何先验信息假设的情况下,根据信号的统计独立特性将源信号从观测混合信号中恢复出来[1]。盲源分离理论[2]最初是由解决“鸡尾酒会”的问题发展起来的,并迅速应用于信号处理[3]、图像处理[4]、自动化等领域[5]。利用盲源分离算法进行信号分选完成了对一定接收时间段内混合信号的分离,但在实际中发射机不断发射信号,接收机会截获到很多时间段内的信号,如何判断分离后的各个信号是否来自于同一信号源,仍需要借助一定的信号分选技术。将隶属于同一源信号的不同时间帧内的信号选出,才能得到完整的源信号。
近年来,跳频信号的分选是研究热点。针对跳频信号分选,大多依据信号的特征参数进行分选。文献[6]提出了利用跳频信号的到达时间进行分选的方法,但只能应用于异步组网的情况。文献[7]提出了利用信号的到达方向来实现跳频网台信号的分选,该方法在干扰严重的情况下分选效果不是很好。文献[8]提出利用盲源分离算法进行跳频网台信号分选,但这种方法只考虑了一帧时间内信号的分选,未实现完整信号的分选。同时,上述算法仅仅针对常规跳频信号进行分离且假设源信号数目已知,而变速跳频信号采用 “跳速多变”的策略加大了利用参数估计实现信号分离的难度。
本文针对上述问题,提出了基于帧重叠的变速跳频信号分选算法。
1 问题概述与模型
1.1 信号模型
定义由接收系统接收到的信号为观测信号,通常其来自一组传感器的输出,其中每一个传感器接收到多个原始信号的一组混合,如图1所示。
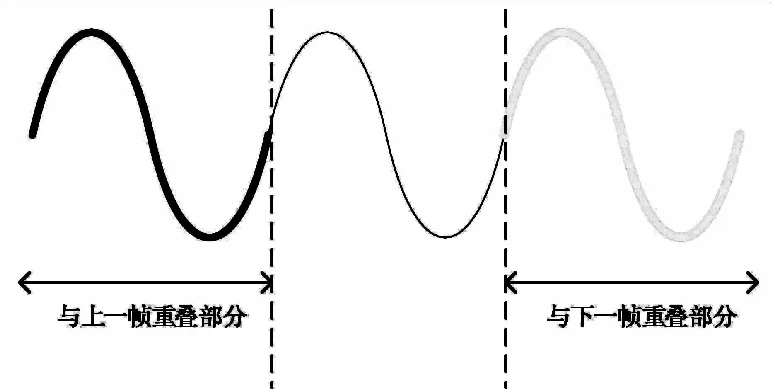
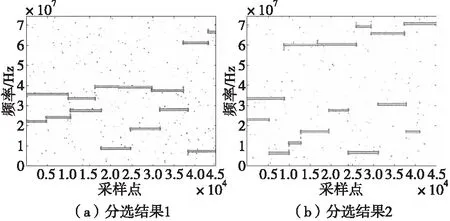
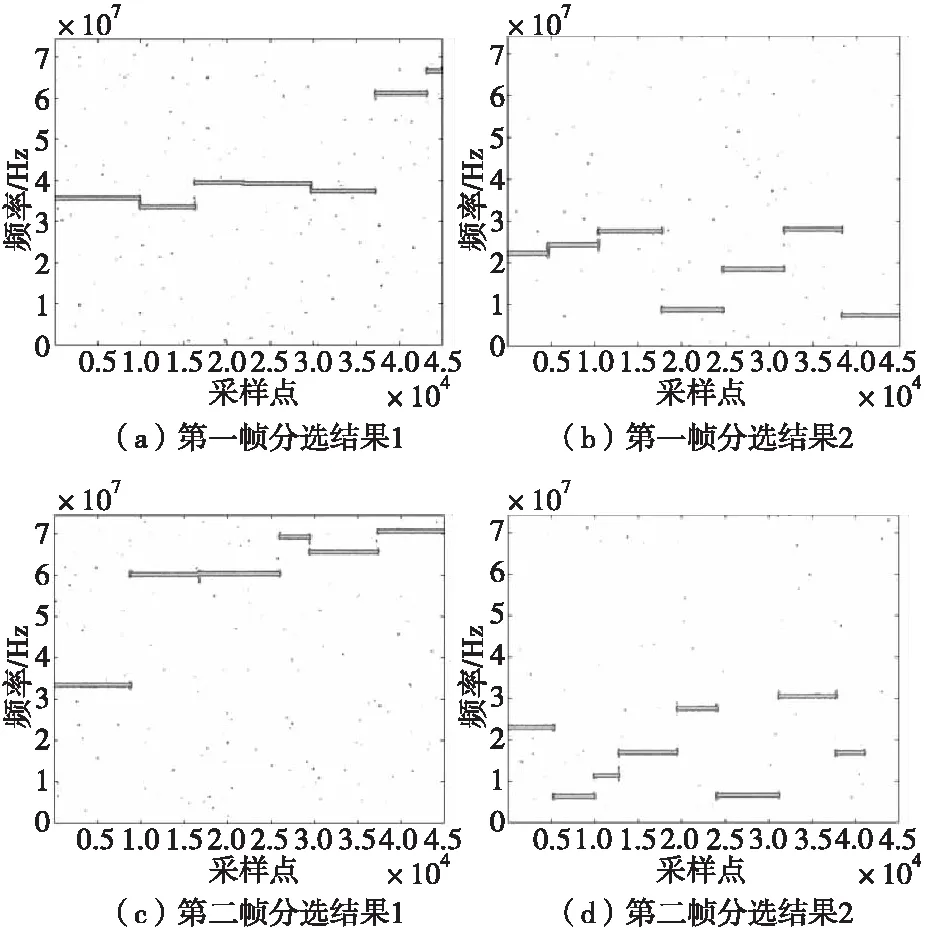
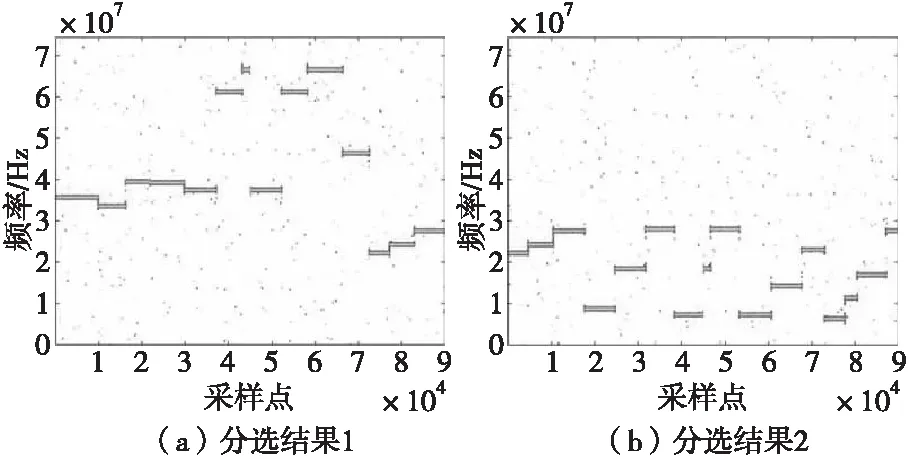
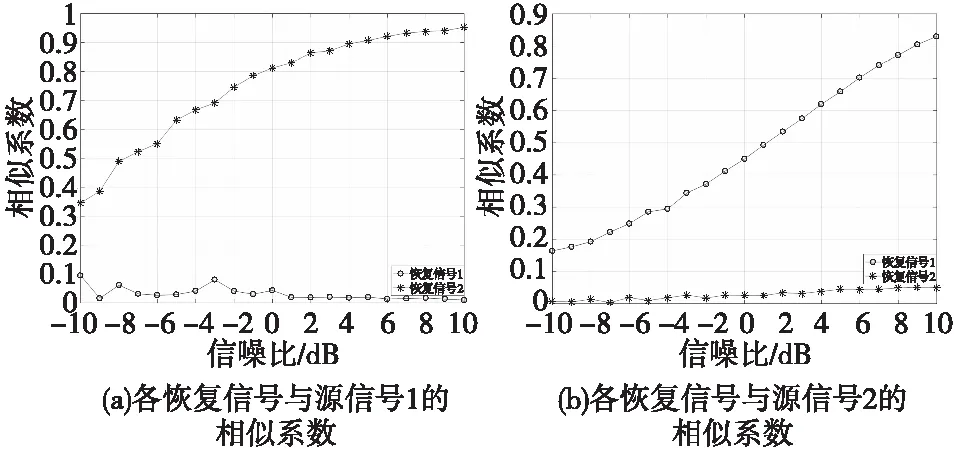
在图1中,N个信号源s1,s2,…,sn(n=1,2,…,N)所发出的信号被M个传感器接收后得到输出观测信号x1,x2,…,xm(m=1,2,…,M),到达角度分别为[θ1,θ2,…,θn],当M 图1 信号接收模型Fig.1 Signal reception model (1) 式(1)中,aij(j=1,2,…,N)为混合系数,ni(t)为第i个传感器的观测噪声,用矢量和矩阵表示为式(2)所示。 (2) 式(2)中,s(t)=[s1(t),s2(t),…,sn(t)]T是N×1的源信号矢量,x(t)是M×1的混合信号矩阵,n(t)是N×1的噪声矢量,A为M×N的混合矩阵,其元素为混合系数aij。 变速跳频信号s(t)与常规跳频信号区别在于跳速的改变,具体体现为其跳频图案驻留时间随机改变,假设变速跳频通信系统的频率合成器可以生成的跳频频率数目为K,同时每一跳拥有不同的跳速,跳速数目为K,则变速跳频系统发射机输出的单个信号可以表示为: (3) 式(3)中,跳频频率为fk(k=1,2,…,K),跳速为tk(k=1,2,…,K),a(t)为信号的基带复包络,φk为信号第k跳的初始相位,gtk(t)为高为1,底边长度为tk的门函数,即: (4) 由于变速跳频信号时域稀疏性不强,将其转化至时频域时可以清晰地观察出数据有明显聚类特性[9],故本文采用短时傅里叶变换(short time fourier transform, STFT)得到变速跳频信号时频域数据。在此基础上进行信号选算法研究。 盲源分离问题的数学模型可以表示为:对M×N维的混合矩阵A设计一个N×M维分离矩阵(或称为解混合矩阵)W,使得其输出信号矢量尽可能独立,即: (5) 算法模型框图如图2。 图2 盲源分离算法模型Fig.2 Blind source separation algorithm model 由于本文针对变速跳频信号进行研究,所以采用短时傅里叶变换(STFT)将信号变换到时频域中进行稀疏化处理,提高信号分选精度,式(2)变为: R(t,f)=AS(t,f)+N(t,f) (6) 帧重叠技术就是在进行相邻两帧信号处理时,对前一帧信号的后半部分数据点结合下一帧数据进行具有一定重叠率的重新采样,使得新的时频域信号包括前一帧信号的部分信号,具有与前一帧信号一定的相似度,从而能够为信号分选提供衡量标准。实际中,大部分的实时宽带频谱仪中采用了重叠FFT技术[10],帧重叠技术的使用有利于宽带信号的实时处理,对于时变信号也可以很好地分析信号的特点,因为信号频谱的时域分辨率得到了提高,一帧频谱的更新时间也会缩短。 重叠帧信号处理的基本思想如图3所示。 图3 帧重叠构建原理图Fig.3 Frame overlap to construct schematic diagram 帧重叠构建原理可以简述为新的一个数据帧对前一个数据帧的数据样点重复进行时频变换,使新的一帧前面部分数据样点中包含上一帧帧尾的部分样点,对比两帧信号之间的相似性,达到不同帧信号的分选,完成信号从分离到分选的过渡。图3中,overlap 为两帧之间重叠点数,可以表征前后两帧信号之间的重叠率。 采用帧重叠技术后,下一帧信号中包含有上一帧信号的部分信息,而这一帧信号的部分信息又被下一帧信号包含,其时域模型如图4所示。 图4 重叠部分时域示意图Fig.4 Schematic diagram of overlapping time domain 图4中,黑色粗线部分代表与上一帧重叠部分,灰色部分代表与下一帧重叠部分。 N个信号根据采样点数可以分为若干帧信号数据,用划分的帧数据表示源数据,则第n路信号的表达式为: (7) 式(7)中,L为源信号所分帧数,d为每帧信号长度。 对原始的分帧数据进行重新时域数据复用的帧重叠技术,式(7)变为: (8) 式(8)中,p为重叠率,其值可由下式得到: (9) 当p=1时,代表信号帧之间没有交叠。 将重叠信号表示为图4中的样式,则式(8)变为: (10) (11) 此时,可以通过对比重叠部分的相似度进行信号分选[11],但是这种计算每帧信号之间相似度是要分别计算各个帧之间的相似度,相当于遍历算法,对于N路L帧信号,算法的运算量高达O(LN),算法性能不佳。 联系变速跳频信号的稀疏特点,将已重叠处理后的信号变换到时频域中进行处理分析,同时,结合盲源分离过程,重叠算法的基本思路为:在前面内容中已提到信号在相邻的帧中不会处于一帧数据的两端点处这一概念的基础上,通过对接收数据的重叠帧进行STFT变化,得到重叠的混合信号时频图,再结合时频分析参数估计理论,对各个跳频重叠帧信号的跳频频率进行估计,得到每个重叠帧信号的频率集;分析相邻重叠信号的频率重叠率,对于重叠率接近p的相邻两帧信号,可以认为来自于一个源信号。不断地对重叠信号进行“STFT+跳频频率估计”,可以依次将各个分离信号拼接在一起,完成分离到分选的过程。 综上所述,在盲源分离背景下的基于帧重叠的信号分选算法步骤如下: 步骤1 针对混合信号进行重叠帧构建,得到多帧混合信号,并根据式(9)计算重叠率p,设置误差参数ε; 步骤2 利用盲源分离算法进行不同帧混合信号的分离; 步骤3 对已分离信号利用其时频图进行频率估计; 步骤4 对比前后帧重叠部分的频率,重叠率记为pi; 步骤5 判断pi与p的大小,若 |p-pi|<ε,则将前后两帧信号去除重叠部分拼接完成分选;若相反,则回到步骤4,直到符合条件; 步骤6 判断迭代次数是否大于分段数,若大于则退出循环;否则回到步骤2; 步骤7 结束算法,得到由多段时间帧组成的分选完整信号。 利用源信号波形和从混合信号中恢复出来的信号波形之间的相似系数[12]来对算法的分选性能进行评价,估计信号源信号的相似系数如下: (12) 实验一 固定信噪比下信号分选 本次实验针对变速跳频信号进行分选研究,采样率设置为150 MHz,截取时长为0.6 ms的观测信号进行分析,STFT采用窗函数为512点的汉明窗,信噪比固定为0 dB,该时间段内各个源信号的参数设置如表1所示。 表1 混合信号参数 首先对0.6 ms时长的混合信号进行分帧,分为两帧时长为0.3 ms的信号,两帧信号时频图分析如图6所示。 图6 两帧混合信号时频图Fig.6 Time-frequency diagram of two mixed signals 分别对两帧信号各自进行盲源分离,得到图7所示分离结果。 图7 两帧分离信号时频图Fig.7 The two frames separate signal time frequency diagram 针对两路变速跳频信号源信号构造三帧重叠帧,重叠点数设置为15 000点,三帧重叠帧时频图如图8所示。 图8 重叠帧信号时频图Fig.8 Overlapped frame signal time-frequency diagram 由于第一帧没有与前一帧重叠部分,故第1帧信号的分选结果如图7(a)所示,现对第2、第3帧重叠帧信号进行分离,得到结果如图9所示。 图9 重叠帧分离信号时频图Fig.9 Overlapping frames separate signal time-frequency diagram 在得到信号时频图的基础上,观察时频图,利用时频分析对15 000点重叠信号的频率进行估计,找出对应的频率重叠的信号,然后去除重叠部分将三帧信号拼接起来,得到图10所示信号分选结果。 观察图10代表的两路分选信号,证明了本文所提算法能够正确对两帧混合信号进行分选,在信噪比为0 dB的情况下,依旧能够较好地完成多段时间帧信号的分离以及分选。 图10 基于帧重叠信号分选结果Fig.10 Sorting results based on frame overlap signal 实验二 不同信噪比下算法性能 为验证本文所提算法的有效性,设置信噪比为-10~10 dB,其余条件不变,进行分选算法,结果如图11所示。 图11 不同信噪比的信号相似系数Fig.11 The signal similarity coefficient of different SNR 观察图11,可以看出信噪比为-10 dB时,信号之间的分离度相差将近20%;当信噪比为10 dB时,信号之间分离程度达到90%以上,证明了本文所提算法在信号分离的基础上,能够解决含噪混合信号的分选问题, 完成了从分离到分选的过渡。 本文提出了基于帧重叠的信号分选算法,该算法在盲源分离的基础上,通过对变速跳频信号进行重叠帧的构建,利用不同时间帧重叠部分的频率相似性,进行不同时间帧的信号分选,能够解决信号的不确定性问题。仿真实验结果表明,本文所提算法在信道条件较差时,依旧有较良好的分选效果,证明了算法的有效性。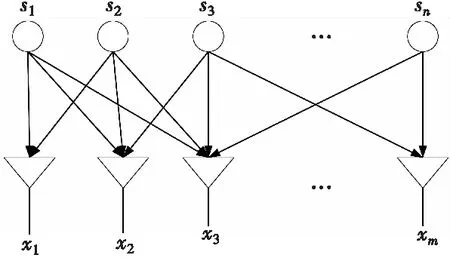
1.2 盲源分离算法模型
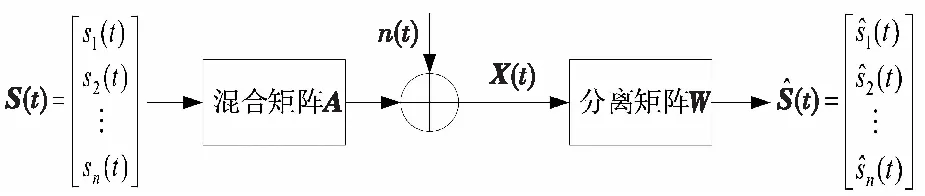
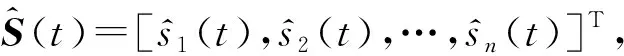
2 基于帧重叠的信号分选算法
2.1 重叠帧的构建
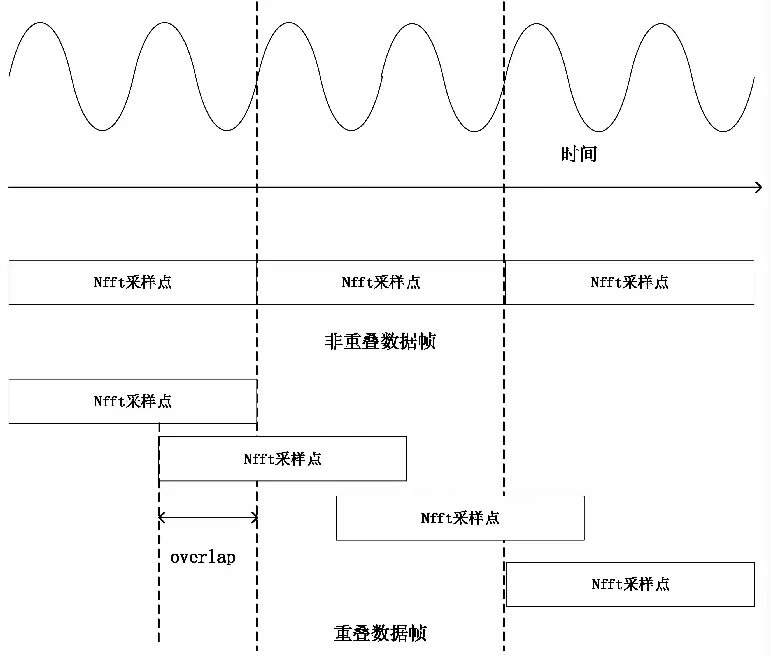
2.2 帧重叠算法原理
3 仿真分析
3.1 算法性能评价指标
3.2 仿真实验



4 结论
