基于VisVSA的容差分配技术在机头前机身对接中的应用

吕培培，葛 磊

(上海飞机制造有限公司，上海 201324)

0 引言

为了保证飞机装配完成后达到规定的飞机结构强度、空气动力性能等性能指标，对装配准确度要求非常高[1]，而装配准确度是控制飞机零组件装配误差累积的有效手段，合理的飞机零组件容差分配是保证飞机装配准确度、控制或补偿装配误差的重要途径，装配误差累计分析与容差优化是获得合理的容差分配方案的关键支撑技术。

国内外学者一直致力于容差分析与分配方面的研究。Lehtihet 和 Dindelli[2]利用 Monte-Carlo仿真法求解非正态分布容差分析。Jean-Yves Dantan和Ahmed-Jawad Qureshi[3]建立了容差分析的数学模型，实现了用量化约束满足和蒙特卡罗模拟方法对容差函数的分析解算。G.Prabhaharan 等[4]将遗传算法和最低成本—容差模型结合起来，提出了基于遗传算法的最优化容差分配算法，克服了传统容差累积分析与综合系统的缺点。

本文基于VisVSA技术，对机头与前机身对接面的协调要素进行容差分配方案设计，得出工艺协调要求、调姿公差、分配给各部段界面公差与装配工艺能力之间的关系图，分析影响各协调要素的主要影响因子，根据目前的工艺能力，确定了一套较优的分配方案。

1 VisVSA应用流程及计算原理

1.1 VisVSA应用流程

VisVSA软件通过动态模拟装配方式近似反映总成零部件在实际装配中的情况。VisVSA本身不能进行建模，需要将CAD数模通过VisVSA自带的模型转化工具导入软件中参与计算。根据尺寸管理流程在产品开发中的一般任务，VisVSA设计出了一套接近实际操作的应用流程，如图1所示。

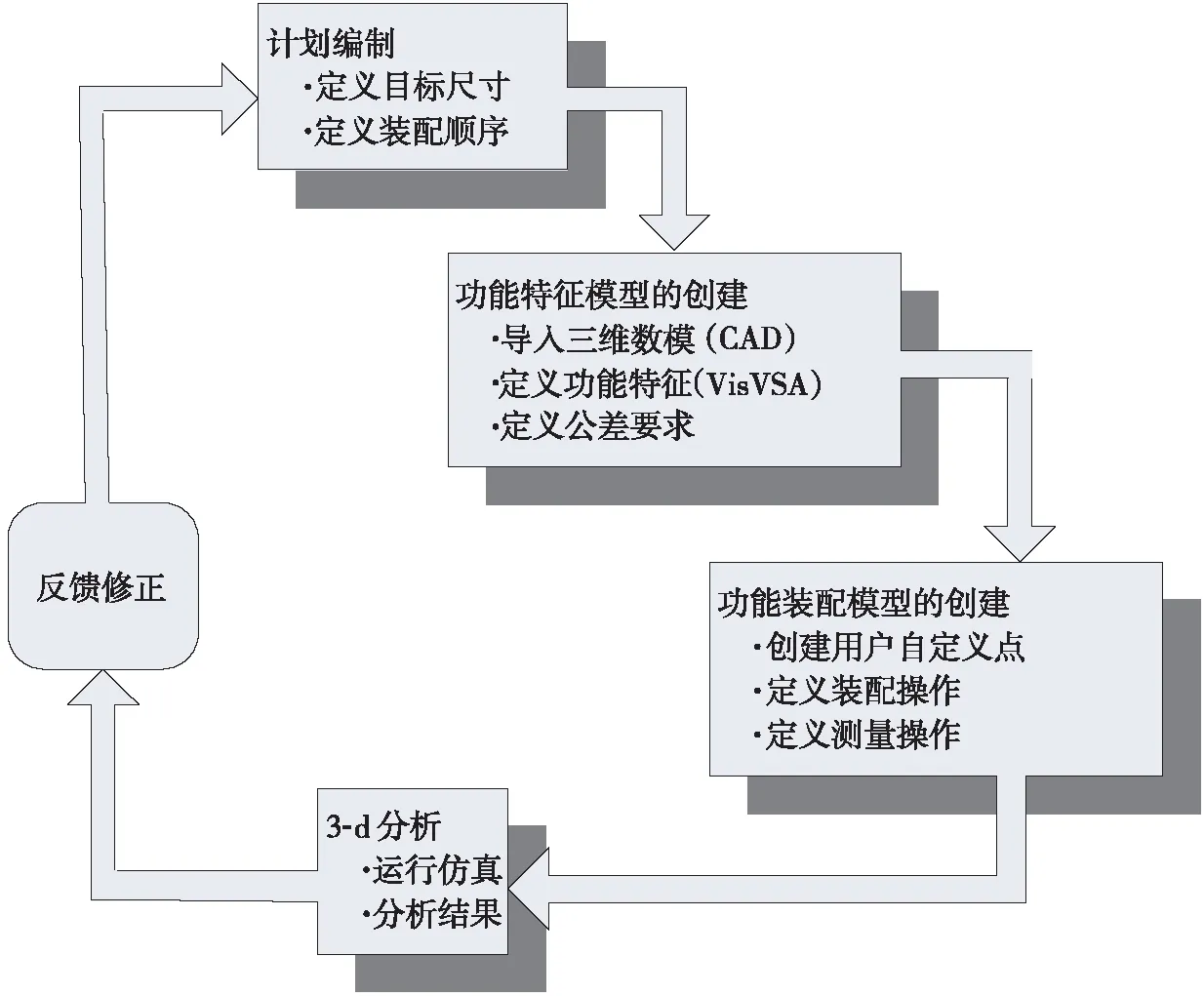
图1 VisVSA应用流程

1.2 计算原理

VisVSA的仿真计算核心采用蒙特卡罗(MonteCarlo)法，这是一种以概率统计理论为指导的数值方法[5]。其基本思想是，当所求解问题是某种随机事件出现的概率或是某个随机变量的期望值时，通过某种“实验”方法，以这种事件出现的频率估计这一随机事件的概率，或者得到这个随机变量的某些数字特征，并将其作为问题的解。正态分布是蒙特卡罗法中使用最广泛的一类模型。通常情况下，如果一个变量受很多相互独立的随机因素影响，而其中每一个因素的影响都很小，则该变量服从正态分布，在自然界和社会中大量的变量都满足正态分布。

2 机头与前机身对接面容差分配方案设计

机头和前机身对接工位协调，需保证对接处机身蒙皮外形要素，确保飞机的气动特性，是飞机装配中典型的外形协调问题，主要表现为对接面间隙及外形阶差。本章节中的数据均为假设数据，以辅助方法流程的阐述。

2.1 基准与定位方法

机头与前机身对接以全机坐标系为基准，用激光跟踪测量地面的TB点，建立基准坐标系，更新带有实际部件协调和计算转换器的伺服系统，以中机身为基准部件，通过测量点和激光反馈执行软件将各机身段调整至参考位置，关闭测量系统并移除标靶和支架，完成最终的定位和对接。

2.2 测量点设置

取机头、前机身蒙皮端面上、下、左、右4个相应的点作为蒙皮间隙的测量点，前机身测量点为其相应位置。间隙测量点的法向为航向(x向)，计算航向的波动。

取机头、前机身蒙皮外形面长桁端头相应的位置作为测量目标，测量点分布仍为上、下、左、右4个点，前机身测量点为其相应位置。阶差测量点的法向为该点所在曲面的切向量，计算周向的波动，如图2所示。

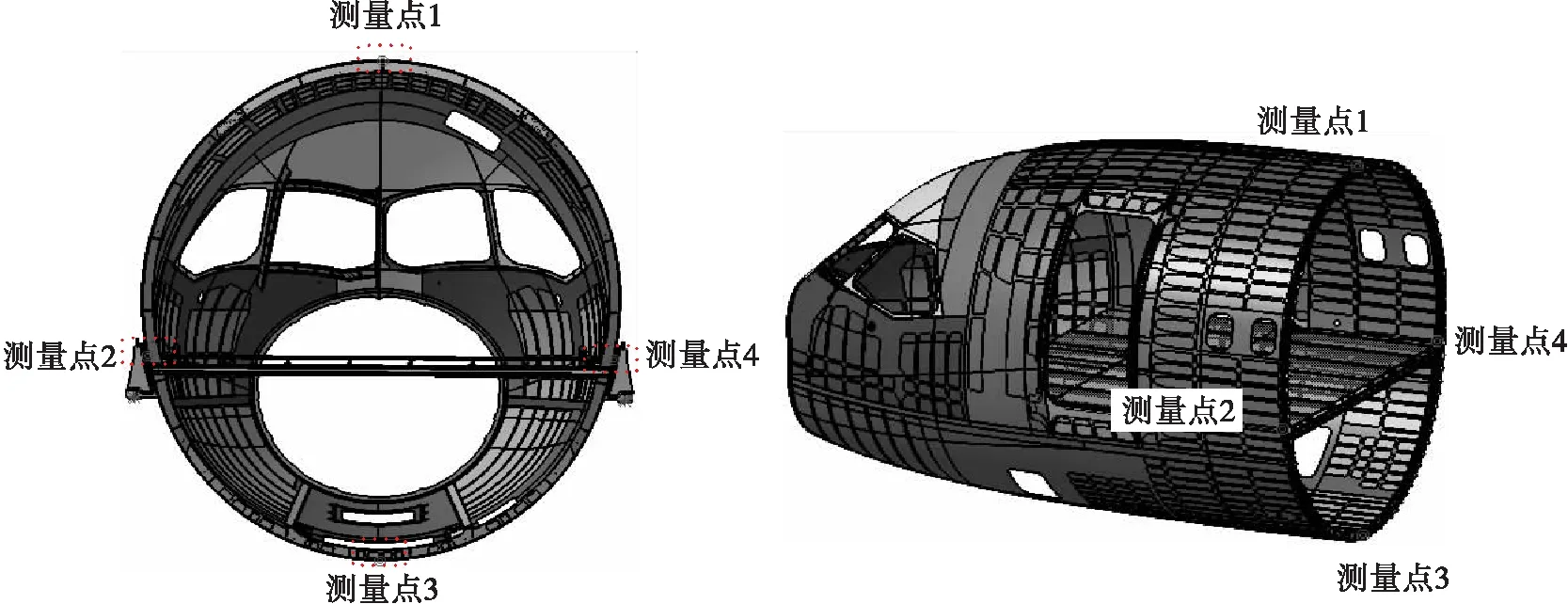
(a)蒙皮间隙测量点 (b)蒙皮阶差测量点

2.3 VisVSA模型建立

1)模型转化。机头、前机身数模转化为jt文件，导入jt文件及调姿点与测量点坐标。

2)定义装配特征。模拟调姿过程，机头、前机身的调姿误差反映在调姿点上，地面坐标系的误差反映在支撑点上。因此，装配特征即为调姿点与支撑点，支撑点通过复制的方式放在工装fixture中，调姿点与支撑点均不设基准，系统默认基准是全机坐标系，符合工艺要求。

3)定义公差值。需要定义调姿点、支撑点公差及各测量点公差，该公差值可调，其调整范围，即优化空间如表1所示，其中调姿点及支撑点公差来源于激光跟踪仪的调姿定位误差及测量误差，测量点公差是根据工程要求分配的值。

表1 公差表

4)创建装配操作。分别装配机头与前机身调姿点到支撑点。

5)创建测量操作。采用补偿缝隙/齐平的方式测量蒙皮间隙、阶差及滑轨端面的相应点。

6)运行仿真。

2.4 结果分析

2.4.1 蒙皮间隙计算结果

固定蒙皮间隙工程要求1.0 mm，蒙皮间隙测量点轮廓度0.5～1.0 mm，以0.05步长，做出分配的蒙皮端面轮廓度与工艺能力指数之间的曲线图，计算数据如表2所示。

表2 蒙皮间隙计算结果

表2数据拟合的曲线如图3所示。

由图3拟合的曲线可知，当蒙皮间隙分别分配给机头与前机身的端面容差为0.48 mm时，工艺能力指数为1.33，即平衡工艺能力(超差率)与成本之间最合适的分配容差是0.48 mm，此时，间隙的概率分布图如图4所示，该图反映了超差情况，超差率为0.007 4%，符合工艺要求。

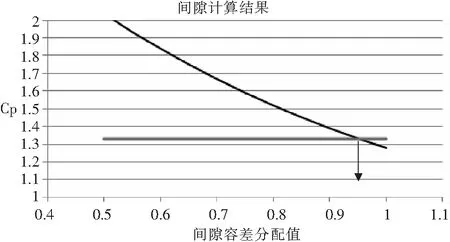
图3 间隙计算曲线图

图4 间隙概率分布图

2.4.2 蒙皮阶差计算结果

固定蒙皮阶差工程要求0.8 mm，蒙皮阶差测量点轮廓度0.5～1.0 mm，以0.05步长，做出分配的蒙皮外形轮廓度与工艺能力指数之间的曲线图，计算数据如表3所示。

表3 蒙皮阶差计算结果

表3数据拟合的曲线如图5所示。

图5 阶差计算曲线图

由图5拟合的曲线可知，当蒙皮阶差分别分配给机头与前机身的容差为0.28 mm时，工艺能力指数为1.33，即平衡工艺能力(超差率)与成本之间最合适的分配容差是0.28 mm，此时，阶差的概率分布图如图6所示，该图反映了超差情况，超差率为0.005 9%，符合工艺要求。

图6 阶差概率分布图

3 结论

容差分配与容差分析在飞机研制过程中起着非常重要的作用，基于VisVSA软件的容差分配具有一定的应用价值。通过机头与前机身的对接实例，验证了该思路与方法的可行性。

1)对于机头与前机身对接面的协调要素，在某个确定的调姿误差下，确定了一套能平衡成本与工艺能力的容差值：即蒙皮间隙分配值为0.48 mm，蒙皮阶差分配值为0.28 mm。

2)容差分配与容差分析相结合的思路可以有效应用于工程实践：首先优化一套较理想的容差分配方案，然后再从零件级的容差分析角度进行验证，容差分配与容差分析相互校验，综合考虑生产工艺能力，权衡其他因素做出取舍，最终得到能平衡大多要素的合理的整机容差分配方案。

综上所述，基于VisVSA的容差分配与容差分析技术可应用于工程实践，具有一定的应用价值。