基于人工蜂群算法的线性系统辨识

林振敏

（中国能源建设集团 江苏省电力设计院有限公司，南京 211102）

0 引言

目前，以传递函数描述的线性系统建模经常采用的方法是：首先，根据系统特性确定模型的形式和阶次；然后，利用系统的阶跃响应曲线，根据不同的传递函数形式，确定相应的模型参数。这种方法实施起来，需要读取响应曲线，误差较大。一般得到参数以后，还需要进一步地调整来确定最终的参数。

群体智能优化算法基于物种的迁移或者进化特性，对需要解决的问题设定目标函数，通过全局搜索能力，得到目标函数的极值。使用较多的群体智能算法主要包括：遗传算法[1]、粒子群算法[2]、蚁群算法[3]等。随群体智能的进一步深入研究，一些其他的优化算法被提出，比如：细菌群体趋药性算法[4-5]、人工鱼群[6]、混合蛙跳算法[7]、狼群算法[8]、布谷鸟搜索算法[9]、人工蜂群算法[10]等。随着群体智能算法的发展，一些学者将智能优化算法应用于线性系统的模型辨识，比如基于粒子群算法的系统辨识[11]。

人 工 蜂 群 算 法（Artificial Bee Colony，ABC） 是 由Karaboga 提出的一种新颖的基于群智能的全局优化算法，其直观背景来源于蜂群的采蜜行为，蜜蜂根据各自的分工进行不同的活动，并实现蜂群信息的共享和交流，从而找到问题的最优解。人工蜂群算法实现简单、寻优能力较强，已经应用于多个领域，比如：故障诊断[12]、参数优化[13]、车间作业调度[14]、聚类[15]等。而在系统辨识领域，人工蜂群算法也有较多的应用，比如：非线性系统参数辨识[16-18]、机器人参数辨识[19]、潜器参数[20]等。

本文针对以传递函数描述的线性系统，提出了一种基于人工蜂群算法的系统辨识算法。该算法利用人工蜂群算法的全局搜索能力，根据给定的阶跃响应数据以及设计的寻优目标函数，得到一组合适的传递函数参数。仿真实验表明，本文提出的辨识方法具有较高的辨识精度。

1 人工蜂群算法

人工蜂群算法包括三种类型的蜜蜂：雇佣蜂、跟随蜂以及观察蜂。其中，雇佣蜂和跟随蜂的数量相同，并且分别占蜂群总数的1/2。每个雇佣蜂对应一个蜂蜜源，这些雇佣蜂的主要工作是寻找并记录与之对应的蜂蜜源。然后，将蜂蜜源的相关信息通过圆摆舞的方式传递给跟随蜂，跟随蜂就根据这些信息来选择蜂蜜源[21]。当雇佣蜂对应的蜂蜜源的位置多次未改变，雇佣蜂变为观察蜂，通过局部搜索确定新蜂蜜源的位置[22]。

在该算法中，每个蜂蜜源位置坐标表示一个可行解。在算法的每一次循环中，雇佣蜂都通过邻域搜索寻找每个蜂蜜源，并计算每个蜂蜜源对应的适应值。根据雇佣蜂传递的信息（即每个蜂蜜源的适应值），跟随蜂通过一定的概率来选择蜂蜜源，并在选择的蜂蜜源周围寻找新的蜂蜜源，并计算它们的适应值及目标函数值[23]。

雇佣蜂和跟随蜂寻找蜂蜜源的公式，如式（1）：

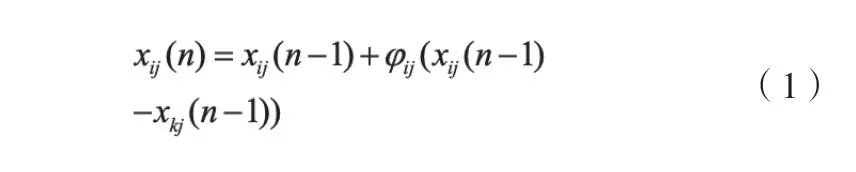
其 中，j ∈{1,2,…,D}，i ∈{1,2,…,N}。N 是 蜜 蜂 源 的个数，D 是每个蜜蜂源的维度，k 是不等于i 的随机索引值，φij是在[-1,1]区间的随机数，xij(n)是蜂群新的更新位置，xij(n-1)是当前位置。如果更新后的蜂蜜源的目标值优于当前蜂蜜源，则利用新的蜂蜜源更新当前的值，否则，保留当前的蜂蜜源值。

跟随蜂选择蜂蜜源的概率为[24]：

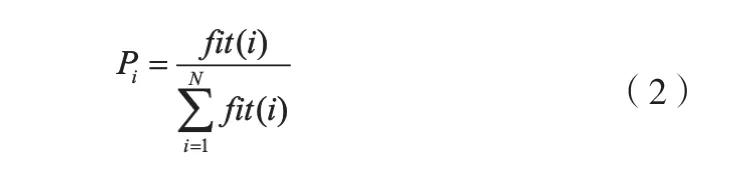
其中：Pi 表示跟随蜂选择蜂源i 的概率，fit(i)是选择蜂源i 所对应的目标函数值。

2 线性系统辨识模型

目前，比较常见的线性系统的辨识模型主要包括如下几类：

1）高阶对象

当求取出的n 不是整数时，用近似的整数代替。

2）多容惯性对象

3）具有纯迟延的高阶惯性对象

4）无自平衡对象

5）零稳态对象

6）逆响应对象

该对象的特点是：在阶跃扰动情况下，系统的输出先朝着与最终趋势相反的方向变化，然后在朝着最终的趋势变化。比较典型的，比如汽包炉的蒸汽量扰动引起的汽包水位的变化、循环流化床锅炉一次风阶跃扰动引起的床温变化等。除了式（8）以外，逆响应系统的传递函数还可描述为：

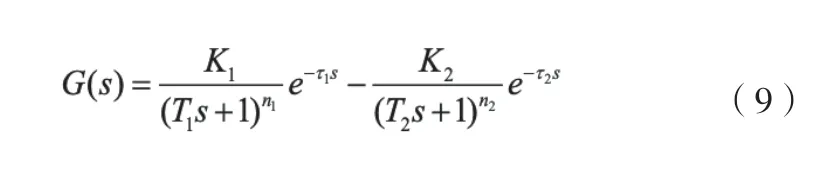
7）高阶有理对象

该对象描述的参数较多，一般不采用这种辨识模型。

3 本文算法

本文提出的辨识算法具体描述如下：

1）选择辨识模型，根据对象特性确定待辨识模型参数的变化区间。

2）确定人工蜂群优化算法的目标函数，一般选择为：

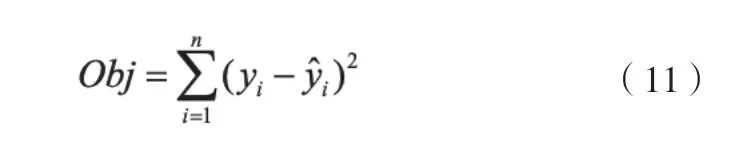
其中，yi为实际输出，为辨识模型输出。

3）初始化蜂群算法的种群个数、蜂源开采次数以及初始种群值，并计算初始种群的适应度（目标函数值）。

4）根据式（1）更新雇佣蜂的值，计算新的适应度值并选择最佳值。

5）判断同一蜂源利用的次数是否超过设定值，如果没有，则根据式（2）计算蜜源被选择的概率，舍弃该蜂源变为侦查蜂并重新初始化蜂源。

6）根据式（1）更新雇佣蜂的值，计算新的适应度值并选择最佳值。

7）判断同一蜂源利用的次数是否超过设定值，如果超过，则舍弃该蜂源变为侦查蜂并重新初始化蜂源。

8）判断人工蜂群算法是否达到了结束条件，如果没有达到结束条件，则转步骤（4）。

9）算法结束后，验证得到的辨识模型是否满足辨识精度要求，如果不满足，则重新进行寻优或者选择新的传递函数形式。

4 仿真实例

4.1 仿真实例1

待辨识模型为：

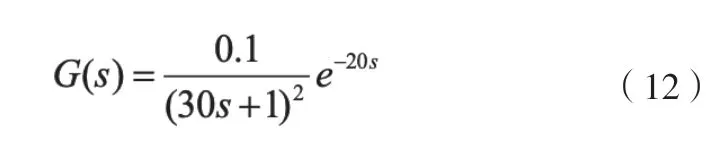
本例采用第一种传递函数形式，原始的数据通过该对象的阶跃响应得到，并在输出的时候，增加了随机分布的白噪声，以模拟现场的测量误差[11]。辨识出的传递函数如下：

图1 显示了实际输出和辨识模型输出曲线。

4.2 仿真实例2

待辨识模型为：

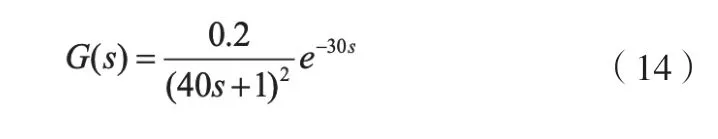
本例采用第二种传递函数形式，原始的数据通过该对象的阶跃响应得到，并在输出的时候，增加了随机分布的白噪声，以模拟现场的测量误差。辨识出的传递函数如下：

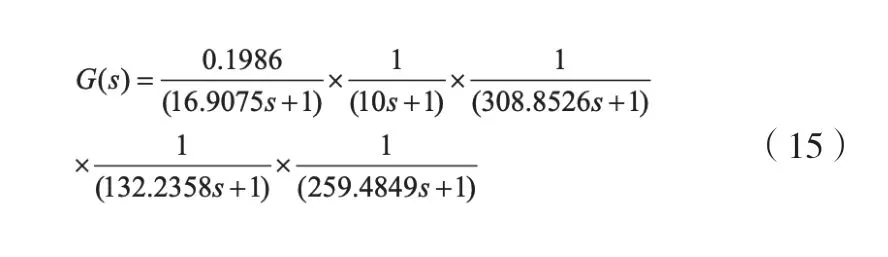
图1 实际输出和辨识模型输出曲线（仿真实例1）Fig.1 Actual output and identification model output curve（Simulation 1）

图2 实际输出和辨识模型输出曲线（仿真实例2）Fig.2 Actual output and identification model output curve（Simulation 2）

图2 显示了实际输出和辨识模型输出曲线。

4.3 仿真实例3

待辨识模型为：

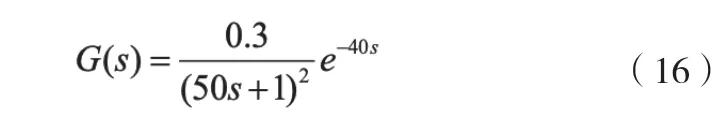
本例采用第三种传递函数形式，原始的数据通过该对象的阶跃响应得到，并在输出的时候，增加了随机分布的白噪声，以模拟现场的测量误差。辨识出的传递函数如下：

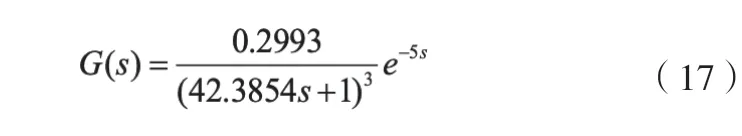
图3 显示了实际输出和辨识模型输出曲线。

图3 实际输出和辨识模型输出曲线（仿真实例3）Fig.3 Actual output and identification model output curve（Simulation 3）

5 结论

本文提出了一种基于人工蜂群算法的线性系统辨识方法，线性系统通过传递函数来描述。人工蜂群算法是近些年发展起来的一种群体智能优化算法，其全局寻优能力强、效率较高，得到了广泛应用。常见的线性传递函数的辨识模型有7 类，在辨识中使用较多的是前3 种，本文通过3个仿真实例，分别验证了前3 种辨识模型。通过比较实际输出和辨识模型输出曲线，本文提出的辨识算法具有较高辨识精度，而模型1 和模型3 的辨识精度更高，在实际中应用也较多。