导波雷达液位计在不同气相介质的误差分析

顾春燕，郭雅山，王浩光，李 苏

（1.江苏核电有限公司 仪控管理处，江苏 连云港 222002；2.山东大学 机械工程学院，济南 250100）

0 引言

导波雷达液位计作为一种新型的雷达式液位计，采用等效采样原理和时域反射原理[1]，适用于低介电常数、高温高压、高辐照等复杂恶劣工况，在现代工业环境中得到了越来越广泛的应用。

但是在部分极端高温高压、高饱和蒸汽工况下，如锅炉汽包和蒸汽分离器，随着温度和压力的升高，液体和蒸汽的介电常数也会发生较大变化。在300℃/10MPa 的环境下，水的相对介电常数会由78.5 降低至18.0，蒸汽的相对介电常数会由1.0 升高至1.5。由于导波雷达液位计应用时域反射原理，蒸汽介电常数的增大会减慢电磁波在导波杆上的传播速度，如果不采取相关的补偿措施，会导致较高的测量误差。

针对该工况下的导波雷达液位计的应用，国外Emerson Rosemount 公司推出了设有“动态蒸汽补偿功能（DVC，Dynamic Vapor Compensation）”的5300 系列导波雷达液位计[2]，国外Endress+Hauser 公司推出了设有“气相自动补偿功能（GPC，Gas Phase Compensation）”的Levelflex 系列导波雷达液位计[3-4]，但均未透露具体的蒸汽补偿算法，且国内相关的研究较少。

因此，本文建立了导波雷达液位计的测量误差与气相介质介电常数关系的函数模型。首先，分析了导波雷达液位计产生测量误差的原因，继而根据时域反射原理建立测量误差与气相介质介电常数关系的函数模型，最后使用食用油代替介电常数发生变化的气相介质进行仿真测量实验。

1 导波雷达液位计的测量原理及特点

1.1 时域反射原理

时域反射原理是导波雷达液位计进行测量的核心原理。导波雷达液位计的表头部分会发射出周期性的电磁波脉冲，电磁波脉冲沿导波杆以光速进行传播。当导波杆上存在阻抗不匹配点时（如液面处），则在该点处电磁波脉冲会产生反射回波，在液面处产生的反射回波沿导波杆进行传播，并被导波雷达液位计的表头部分接收。由于电磁波脉冲的发射和接收时间与导波雷达液位计的表头和液面的距离成正比，因而由电磁波脉冲的传播时间，即可计算出被测液位高度。

1.2 导波雷达液位计的特点

由于导波雷达液位计应用时域反射原理和等效时间采样原理，且为接触式测量仪表，因而，与一般的液位计相比，导波雷达液位计有其原理上的优势。导波雷达液位计的特点如下：

1）可靠性高。导波雷达液位计采用时域反射原理，其测量过程只与被测介质的介电常数有关，而与密度、压力等无关；电磁波在导波杆上进行传播，与天线式雷达液位计相比，电磁波信号在传播过程中产生的损耗较小，有质量更好的回波信号。因此，高温高压、泡沫和粉尘等复杂工况对导波雷达液位计产生的影响极小，提高了导波雷达液位计测量的可靠性[5]。

2）测量精度高。导波雷达液位计采用等效时间采样原理，可以实现回波信号在时间轴上的精确放大，测量误差最小可以控制在±1mm，具有很高的测量精度。

3）安装和维护方便。导波雷达液位计的表头和导波杆部分为分体式设计，在面对不同的测量工况时，可以根据需要选择导波杆的类型，如杆式、缆式和同轴式，并且可以通过电缆连接导波杆和表头实现远传测量，安装方便；导波雷达液位计采用两线制回路供电，液位计表头及导波杆无可动部件，后期维护量较少。

2 测量误差分析

2.1 测量误差原因分析

在极端高温高压、高饱和蒸汽工况下，蒸汽的密度和温度会增大，导致蒸汽介质的介电常数增大。根据时域反射原理，当气相介质的介电常数增大时，电磁波脉冲的传播速度会相应减慢，使得测得的电磁波脉冲传播时间增大，导致测得液位位置低于实际液位位置。

2.2 测量误差与气相介质介电常数关系模型的建立

由时域反射原理可知：在理想的测量工况下，电磁波脉冲的传播时间t 与液位计表头和至液面的距离L 有以下关系式近似成立：

公式（1）中：ε 为气相介质的相对介电常数；c 为电磁波在真空中传播速度。

则根据公式（1），导波雷达液位计根据测得的传播时间t，计算得到的测得液位距离l 和实际液位距离L 有以下关系式近似成立：

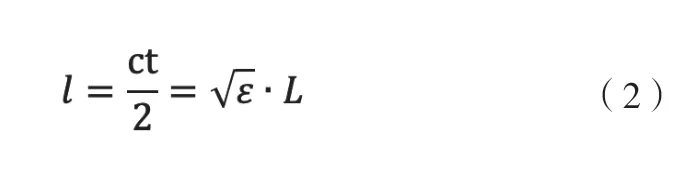
因此，可以得出测量误差与气相介质的介电常数的关系模型为：

则根据公式（3），在正常测量工况下，空气的相对介电常数可以视为1.0，因此可以忽略空气对于测量的影响。但是，当气相介质的介电常数发生较大变化时，如在高温高压、高饱和蒸汽工况下，气相介质的相对介电常数可以升高至1.5，则根据公式（3）可以计算，在该工况下进行测量会产生22.5%的测量误差。

3 实验验证

考虑到高温高压、高饱和蒸汽工况下气相介质的介电常数较为不稳定，且该工况的调控较为困难，具有较高的危险性，本文采用食用油（相对介电常数大于空气）填充容器内液面上方的空间，模拟介电常数发生变化的气相介质，对测量误差与气相介质介电常数关系模型进行验证。

在实验过程中，为方便距离的计算，以导波杆上的法兰盘为零坐标基准，坐标轴方向从法兰盘至导波杆末端。依次采集液位位置L 为550mm、600mm、650mm、700mm、750mm、800mm 时的回波信号，每个液位位置下采集20 组回波信号。在液面上方添加食用油，重复在每个液位下采集20 组回波信号。在MATLAB 中对回波信号进行处理，包括以下5 个步骤：

1） 回波信号的预处理。使用巴特沃斯滤波器，滤除回波信号中的高频噪声。

2） 回波信号的识别。根据回波信号的特点，在一定横坐标范围内，查找幅值最大点所在的位置作为回波信号的位置。

3） 回波信号的定位点的选择[6]。在回波信号的峰值点处使用二阶拉格朗日插值，将插值后的横坐标作为回波信号的定位点，以获取更高的测量精度。

4） 液位-传播时间关系的确定。根据导波雷达液位计的等效时间采样原理，确定在正常工况下测得的传播时间与对应液位的关系。

5） 液位值的标定。对根据测量时间计算得到的液位进行标定处理。

对回波信号进行处理后，测得的实验数据见表1。

从表1 可以看出，当液面上的介质由空气变化为食用油时，液位测量误差很大，且测量相对误差较为稳定，与液位实际距离无关。

考虑到所使用的食用油（玉米油）在常温常压下相对介电常数约为2.8 ～3.4，故根据公式（3），可以计算出测量误差约为67.3%～84.4%，与表1 中测得的实验结果较为符合。

4 结束语

为了研究导波雷达液位计在气相介质介电常数发生变化时产生的测量误差，按照导波雷达液位计使用的时域反射原理出发，分析了在气相介质发生变化时导波雷达液位计产生测量误差的原因，并建立了测量误差与气相介质介电常数关系的函数模型。

通过在液面上添加食用油，模拟介电常数发生变化的气相介质，对该函数模型进行了验证，实验结果与函数模型较为符合。

表1 液位计测得距离Table 1 Distance measured by GWR