融合用户满意度的产品需求配置方法研究

张迪婧，侯增选，黄 磊，赵有航

融合用户满意度的产品需求配置方法研究

张迪婧，侯增选，黄 磊，赵有航

(大连理工大学机械工程学院，辽宁 大连 116024)

为合理地确定用户需求偏好及其优先程度以适应大规模定制生产模式，最大限度提升用户满意度，提出一种改进的产品用户需求配置方法。将模糊聚类分析方法融入Kano模型中对用户需求进行归属分类，根据用户需求对满意度提升的贡献程度进行筛选，计算需求满意度及重要度评价因子，建立产品用户需求递阶层次结构模型。在模糊层次分析法(FAHP)中通过采用模糊最优最劣法(FBWM)构造一致性三角模糊数互补判断矩阵，引入可能度概念实现去模糊化，得到用户需求初始权重，并将需求评价因子作为初始权重的修正因子，将修正后的权重进行归一化处理，得到用户需求综合权重，以此为依据实现产品需求配置。以某企业眼镜产品设计开发为例，验证了该方法的有效性，为眼镜及其他产品设计开发提供了用户需求配置策略。

用户需求；需求配置；用户满意度；Kano模型；模糊层次分析法；定量化

近年来，随着人们消费理念的转变，用户需求呈现多样化、差异化的发展趋势。卖方市场主导下的大众化产品和有限的产品配置方式难以满足消费者日益主动和强势的个性化需求。在现代网络信息技术和先进制造技术的推动下，以用户为驱动，以产品多品种、高质量、低成本和短生命周期为特征的大规模定制(mass customization，MC)生产模式，逐渐成为一种全新的战略思维。这种生产模式在企业大规模生产(mass production，MP)的基础上[1]，融合了用户的个性化需求，以平衡用户需求项增多引发的用户满意度和企业生产成本之间的矛盾。用户对需求的表述具有模糊性、动态性和不确定性的特点，往往表达为满意度。因此，如何有效地进行用户需求识别及配置，以期最大限度上提升用户满意度是大规模定制发展所必须解决的问题。

卡诺模型(Kano model)[2]通过用户偏好分类技术识别用户需求和期望，研究了产品质量属性与用户满意度之间的相关性，已成为产品设计和新产品创意生成过程中反映用户满意度的有效方法，但传统的Kano模型侧重于产品质量属性分类方法及各类关系曲线的定性描述，未明确说明同一类别质量属性的满意度及重要度的优先顺序，为此国内外学者对Kano模型的量化方法及应用展开研究。张文召等[3]提出一种结合粗糙集与Kano模型、灰色关联分析与逼近理想解排序法的产品设计方案决策方法，实现了多目标决策要求下方案的优选。ZHAO等[4]提出了通过确定用户需求和用户满意度之间的关系来量化Kano模型，可将需求映射阶段和产品配置设计阶段联系起来。SUH等[5]基于Kano模型推导了校企合作活动中各因素的满意度指数、不满意度指数和潜在顾客满意度改进指数，为校企合作提供指导方针。DOU等[6]提出了一种结合Kano模型和交互式遗传算法(interactive genetic algorithms，IGA)的方法，在充分考虑客户的个人偏好的同时增强有效的用户参与度，实现客户驱动的产品定制设计。考虑到用户需求表述的模糊性，AVIKAL等[7]提出了一种将模糊Kano模型集成到QFD中以确定SUV汽车外形美学属性的分类和排序方法，并与经典Kano模型进行对比，验证了该方法的有效性。目前针对Kano模型的方法与应用研究仍存在不足：①多数学者采用频数最大法确定产品质量属性的归属类别，易出现不同Kano类别频数相近或相等的情况，影响类别判定的准确度；②模糊Kano模型虽在用户需求表述上更贴合模糊性的特点，但其问卷专业性更强，增加了问卷及调研难度，影响结果的有效性；③多数Kano问卷未区分各质量属性的权重，即默认其在整体评价中具有相同的重要程度，不能反映用户间的差异性。模糊聚类分析法采用模糊数学的方法处理聚类问题，可得到样本隶属于各类别的不确定程度，更能客观的反映现实世界，成为聚类分析研究的主流。模糊聚类分析法与Kano模型相结合为类别划分提供了新思路，能有效规避Kano模型中可能存在的质量类别判定不准确的问题[8]。通过对Kano问卷结构的改进，设置产品质量属性用户赋权项，可反映不同用户的评价差异，使评价结果更准确。

用户需求的重要度反映了其在产品设计综合决策过程中占有的地位和用户对产品的关注程度，对已确定的用户需求进行优先级排序是需求配置的关键环节。层次分析法(analytic hierarchy process，AHP)将定性与定量分析相结合，广泛应用于优先级排序及多目标、多准则、多层级的方案评估决策，但传统的AHP无法反映决策者判断的模糊性，并且决策过程中构造的判断矩阵一致性检验困难、一致性判断标准(<0.1)缺乏理论依据，为此一些学者引入模糊逻辑，扩展成模糊层次分析法(fuzzy analytical hierarchy process，FAHP)，提高了决策的客观性和可靠性。SHAMEEM等[9]应用FAHP对全球软件开发环境中用于扩展敏捷开发的障碍进行优先排序和分类。KUTLU和KAHRAMAN[10]将传统的AHP扩展到球形模糊层次分析法，并应用于可再生能源的选址问题中。LYU等[11]研究了一种梯形FAHP，采用梯形模糊数表示评估因子之间的相对重要性，用于评估与地面沉降有关的特大城市基础设施的风险。目前FAHP方法在优先级排序中存在以下不足：①传统的FAHP需通过专家将决策方案进行两两对比构造模糊判断矩阵，比较次数多，尤其当决策方案数量较大时，评估过程复杂繁琐，影响评估的有效性；②采用模糊数构造的模糊判断矩阵往往不满足一致性，一致性检验困难，修正过程繁琐。模糊最优最劣法(fuzzy best-worst method，FBWM)[12]是在最优最劣法(best-worst method，BWM)[13]的基础上，考虑专家决策的模糊性和不确定性，引入模糊理论的一种最新的多属性决策方法。FBWM通过专家选定最优、最劣指标并执行最优指标相对于其他指标及其他指标相对于最劣指标间的参考比较，建立模糊最优、最劣比较向量，减少了专家决策过程中的比较次数，简化了评价过程。将FBWM用于FAHP中模糊一致性互补判断矩阵的构建，可避免一致性检验导致的结构冗余，简化优先级排序算法。

针对目前用户需求类别划分及优先级排序过程中存在的不足，本文提出一种改进的产品用户需求配置方法，通过建立模糊性、不确定性、定性化的用户需求与集专家评估与用户评估于一体的需求定量化表述之间的映射模型，实现产品需求配置。

1 研究框架

本文提出一种改进的产品用户需求配置方法，具体流程如图1所示，将FAHP法融入Kano模型中对用户需求进行归属分类，计算用户需求评价因子，建立产品用户需求递阶层次结构模型。在FAHP中通过采用FBWM构造一致性三角模糊数互补判断矩阵，以三角模糊数[14]代替模糊判断矩阵中的确定值，引入可能度概念实现去模糊化，得到用户需求初始权重，并将用户需求评价因子作为初始权重的修正因子，计算用户需求综合权重，从而实现用户需求定量化的优先级排序，以此作为产品用户需求配置的指导。

图1 融合用户满意度的产品需求配置方法

2 基于Kano模型的用户需求获取方法

将模糊聚类分析方法融入Kano模型，对用户需求进行识别、分类、筛选，采取用户角度的需求重要度和Kano满意度调整系数进行需求量化分析，并构建用户需求递阶层次结构模型。

2.1 产品用户需求特征识别

用户需求信息通常呈现多面性、差异性、动态性、模糊性、犹豫性和主观性的特点，且有些需求是用户难以想到的惊喜需求[15]。为获取较全面的用户需求，采用资料查询、深度访谈、用户消费心理问卷调查综合调研方法，识别用户需求特征并筛选得到初始用户需求。

2.2 产品用户需求特征归属分类

对初始需求进行编号并设计评价问卷，采用FAHP法进行需求类别判定，步骤如下：

(1) 对用户需求设置正反向问题，分别测试用户在面对具备或不具备某项特征时的满意度情况，并由用户对需求特征的重要程度打分。以眼镜“尺寸可选择”为例，问卷内容见表1。

(2) 图2为Kano模型，其将质量属性分为5类，对应5种用户需求。根据表2进行问卷分析，得到用户需求特征的Kano类别隶属度。

(3) 根据需求特征Kano类别隶属度，采用模糊聚类分析方法对其进行归属分类，步骤如下：

图2 Kano模型

表2 Kano模型评价标准

(注：A为魅力型需求；O为期望型需求；M为必备需求；I为无差异需求；R为反向需求；Q为有问题的回答，对应的问卷视为无效)

步骤1.设论域={1,2,3,cr}为产品初始用户需求特征集合，任一需求向量可表示为=(cr1, cr2, cr3, cr4, cr5)，=1,2,3,···,，其中cr1~cr5分别代表该需求特征对A，O，M，I，R的隶属度，据此建立隶属度矩阵，并采用平移极差变换法进行标准化处理，即

其中，r为cr和cr间的相似程度；为修正系数，取值为(0,1)，保证rÎ[0,1]。

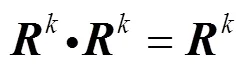
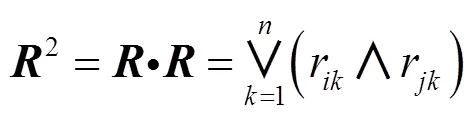
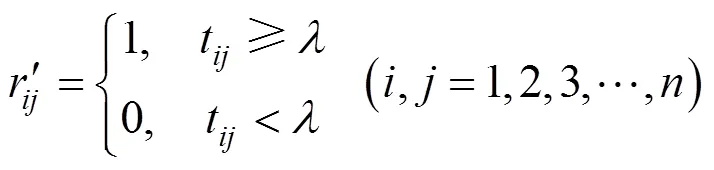
2.3 产品用户需求特征筛选

由Kano模型可知，不同用户需求特征对用户满意度的提升程度和受关注度不同，因此需进行需求筛选，筛选类别分为M，O，A，I，R。其中M类需求是产品的基本标准，被视为理所应当的先决条件，是产品的基本属性，为简化需求分析过程，在产品需求配置过程中应予以剔除；O类需求的用户满意度与需求的满足程度成正相关，应关注并保留，以提升产品的整体满意度；A类需求能最大程度上提升用户整体满意度，并给用户带来惊喜，可提升产品在其竞品中的影响力和竞争力，成为“卖点”，应重点关注并保留；I类需求基本不影响用户满意度；R类需求对用户满意度产生负面影响，均应剔除。

2.4 产品用户需求量化分析

(1) 根据表1构建用户需求重要度向量=(1,2,···,r)T，其中r为第项需求重要度均值。

(2) 在Kano模型中，用户需求实现程度与用户需求满意度之间的关系可用含参函数近似量化，即

其中，为用户满意度；为用户需求实现程度；c为常数；为Kano模型中的调整系数，不同Kano类别对应不同的值(人为确定)：A类需求取>1，O类=1。

(3)根据r和值确定用户角度的需求评价向量=(1,2,···,e)T，其中评价因子为

2.5 产品用户需求递阶层次结构模型的构建

采用KJ法，按照各用户需求间的亲和性，对其进行归纳整理，构建用户需求递阶层次结构模型，用框图表示层级间的递阶结构和用户需求的从属关系，并重新编号。

3 基于FAHP的用户需求配置方法

为改善人类思维模糊性、不确定性带来的信息失真，减少专家对各指标的比较次数，避免一致性检验导致的结构冗余，在FAHP中采用FBWM构造一致性三角模糊数互补判断矩阵，引入可能度概念，计算用户需求初始权重，结合Kano需求评价因子，得到综合权重，实现用户需求定量化的优先级排序，据此进行产品用户需求配置。

3.1 模糊最优、最劣比较向量的构建

(1) 有个专家参与产品用户需求重要度排序，根据用户需求递阶层次结构模型，设某准则下的用户需求为={1,2,···,x}，专家根据市场竞争环境综合评估，确定最优指标x和最劣指标x。

(2) 进行用户需求重要度模糊参考对比，包括最优指标与各项指标间的成对比较，以及各项指标与最劣指标间的成对比较，采用0.1~0.9标度法描述任意2项指标的相对重要程度，0.1表示极端不重要，0.9为极端重要，0.5为同样重要，评价值以三角模糊数形式表示。设第个专家构建的模糊最优、最劣比较向量分别为

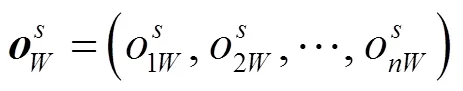
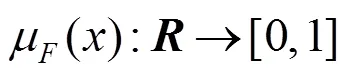
且0<≤≤，则称为三角模糊数。

(3) 将个专家构造的向量进行整理，得到新的模糊最优比较向量=(a1,a2,···,a)和模糊最劣比较向量=(1W,2W,···,a)，其中a，a分别为整理后的最优指标相对于第项指标和第项指标相对于最劣指标的重要度，即

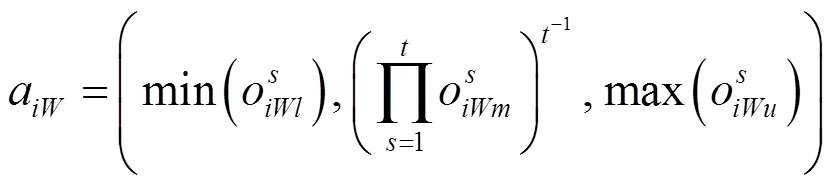
3.2 一致性三角模糊数互补判断矩阵的构建

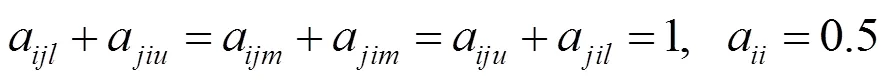
则称矩阵为三角模糊数互补判断矩阵。

则称矩阵为完全一致性三角模糊数互补判断矩阵。

3.3 产品用户需求初始权重计算

为便于决策，需根据一致性三角模糊数互补判断矩阵，并计算矩阵中各决策指标的排序向量，但模糊数形式不能直观地反映数值的大小，需通过去模糊化方式将其变换为确定值。将三角模糊数运算法则与可能度概念结合，给出某项准则下用户需求初始权重计算的方法：

(1) 计算各项用户需求在某项准则下的模糊综合评价值

(2) 三角模糊数之间的比较需通过计算某一模糊数大于另一模糊数的可能性程度来实现，即可能度，见定义4和5。

定义4[19].设1=(1,1,1)，2=(2,2,2)为任意三角模糊数，则1≥2的可能度为

定义5[19]. 设为任意模糊数，则大于其他个模糊数的可能度为

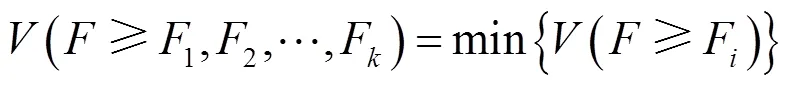
其中，=1,2,···,。

根据定义4和5计算用户需求x的模糊综合评价值S大于其他各项用户需求的可能度，将其作为用户需求x的权重，记为(x)。由此可得到各项用户需求权重向量为

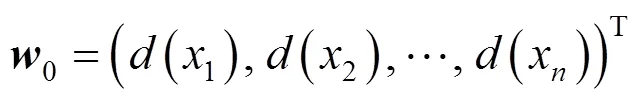
(3) 将0归一化，得到产品用户需求初始权重向量=(1,2,···,w)T，其中

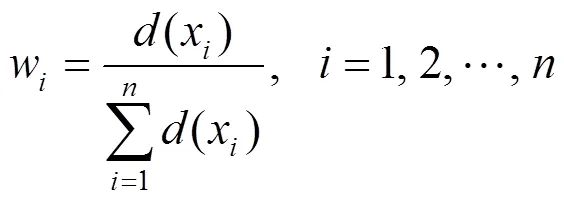
3.4 基于Kano模型的用户需求权重调整

在产品需求配置过程中，A类需求往往不易被用户察觉，一般初始权重较低，但对提升用户满意度的贡献率却很大，因此对不同类别的用户需求需设置不同权重加以修正。为优化产品需求配置过程，需将式(6)中Kano决策的需求评价因子e作为用户需求初始权重w的修正因子。

3.5 产品用户需求优先级排序

3.6 产品用户需求配置

根据用户需求优先级排序，合理选取重点需求并结合实际情况进行需求配置。该配置方法将专家评估与用户评估结合在一起，既能保证需求优先级排序的权威性、可靠性，使产品需求配置具备可行条件，又能保证需求优先级排序的真实性、准确性，真正实现用户驱动的产品用户需求配置。

4 实例研究

随着用户消费观念的转变和消费心理的成熟，眼镜已不单是矫正视力或保护眼睛的工具，逐渐成为能够表达情感、彰显个性的时尚产品。作为劳动密集型产业的代表，眼镜在中国乃至全球有庞大的消费群体，市场竞争激烈。本文以深圳某眼镜公司设计开发用户驱动的眼镜产品为例，运用本文方法进行需求识别与配置，并验证了该方法的有效性和可靠性。

通过相关资料查询、对眼镜用户及销售人员、设计人员进行深度访谈、对眼镜用户进行消费心理问卷调查，将搜集到的需求特征进行筛选、归类、编号，见表3。

表3 眼镜初始需求特征

采用表1所示的问卷对上述需求进行调研。为最大限度覆盖眼镜用户群体，选取包含眼镜使用者及从事眼镜行业的销售人员在内的群体作为调研对象，发放问卷500份，回收有效问卷482份，有效回收率96.4%。采用SPSS 25.0对问卷中22个需求项的满意度及重要度分别进行信度分析，见表4，其中各需求项的Cronbach's Alpha值均大于0.9，说明问卷数据信度质量很高。此外，校正项总计相关性(corrected item-total correlation，CITC)均大于0.4，说明各需求项与总体之间具有良好的相关关系，信度水平良好，因此问卷设计可靠性良好。

表4 信度分析

对照表3建立用户需求特征的Kano类别隶属度矩阵

采用MATLAB数学软件进行模糊聚类分析，将需求特征进行Kano归属分类并生成图3所示的眼镜初始用户需求特征动态聚类图，当=0.6184时，可将需求特征分为4类，结果见表5。

表5 眼镜初始用户需求特征Kano归属划分

将M，I类需求剔除后，根据表1问卷结果，构建用户需求重要度向量=(3.49,3.45,3.95,3.59, 3.78,3.41,4.18,4.16,3.84,4.15,4.04,4.03)T，并由研究人员确定Kano模型中的调整系数：A类需求取=2，O类取=1。根据式(6)确定用户角度的需求评价向量=(0.0828,0.0818,0.0937,0.0851,0.0448, 0.0809,0.0991,0.0987,0.0911,0.0984,0.0958,0.0478)T，表示用户角度眼镜需求量化分析结果。

采用KJ法建立最终的眼镜需求递阶层次结构模型，对各层次指标进行编号，如图4所示，分别对准则层和指标层采用本文提出的基于FAHP的用户需求配置方法完成眼镜用户需求权重计算。以准则层为例，评审专家综合评估得出最优指标和最劣指标分别为美观性B2和友好性B3，采用0.1~0.9标度的三角模糊数确定模糊最优、最劣比较向量为

图4 眼镜用户需求递阶层次结构模型

Fig. 4 Hierarchical model of eyewear user demands

构造3×3的方阵，将上述向量中的三角模糊数填入方阵对应位置，如a1表示最优指标美观性B2相对于舒适性B1的重要程度，填入方阵第2行第1列位置，根据定义2可补充互补的三角模糊数，并根据定义3进行方阵补全及调整，使其满足一致性，完成一致性三角模糊数互补判断矩阵的构造

根据式(14)~(18)，在MATLAB数学软件中计算得到准则层指标的初始权重

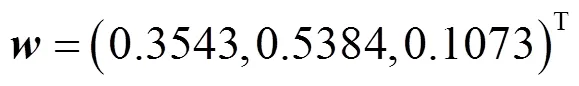
同理可计算各准则下用户需求初始权重，根据层级关系将初始权重进行归一化处理，并将Kano决策中的需求评价因子作为初始权重的修正因子，得到眼镜用户需求综合权重，并给出需求优先级排序，见表6。

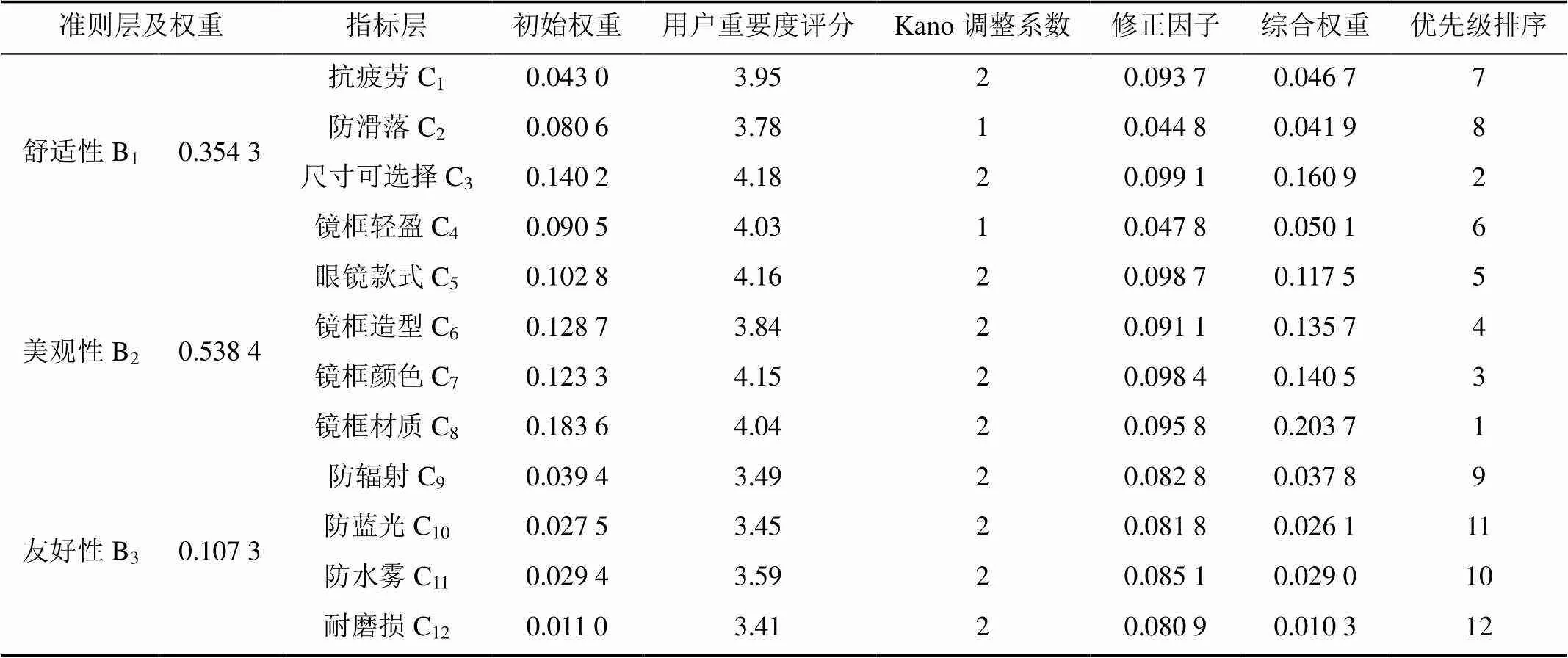
表6 眼镜用户需求综合权重及优先级排序

结果表明，准则层3类评价指标的优先级排序为：美观性B2>舒适性B1>友好性B3；指标层12项评价指标的优先级顺序为：镜框材质C8>尺寸可选择C3>镜框颜色C7>镜框造型C6>眼镜款式C5>镜框轻盈C4>抗疲劳C1>防滑落C2>防辐射C9>防水雾C11>防蓝光C10>耐磨损C12，其中前5项需求更受用户青睐，需在眼镜产品设计开发过程中，保证必备需求的前提下，将前5项需求作为设计重点，剔除综合权重占比小的需求。该排序结果反映了融合用户满意度的用户偏好信息，为眼镜用户需求配置提供了指导性建议：

(1) 除满足眼镜基本的功能需求外，眼镜的美观性成为提升用户整体满意度的首要指标，因此未来的眼镜设计需融入更多美学因素，成为凸显用户个性、时尚的标签。

(2) 眼镜镜框材质、颜色、造型及眼镜款式是影响眼镜美观性的主要因素，由于用户需求的复杂性及多样性，进一步深挖不同材质、颜色、造型及款式对用户满意度提升的影响，细化用户需求，才能为设计师后续方案设计提供更全面、准确的指导。

(3) 用户注重眼镜佩戴的舒适性，其中“尺寸可选择”对用户的重要性十分显著，因此未来的眼镜设计应根据用户面部特征信息进行定制，真正做到眼镜“量身定制”。

(4) 为促进眼镜行业向大规模定制生产模式的转型，平衡用户需求项的增多引发的用户满意度和企业生产成本之间的矛盾，需针对权重较大的需求项进行定制并批量生产，以保证多数用户的需求，同时可面向少数用户提供高端个性化定制服务，以期覆盖不同的消费群体。

5 结束语

为合理地确定用户需求偏好及其优先程度以适应MC生产模式，最大限度上提升用户满意度，本文提出一种改进的产品用户需求配置方法，通过建立模糊性、不确定性、定性化的用户需求与集专家评估与用户评估于一体的需求定量化表述之间的映射模型，实现产品需求配置。本文将模糊聚类分析方法与Kano模型结合进行用户需求类别划分，通过设置产品质量属性用户赋权项改进Kano评价问卷结构，解决了质量类别判定不准确的问题，反映了不同用户的评价差异，使评价结果更准确；将FBWM与FAHP结合，减少了专家决策过程中的比较次数，避免一致性检验导致的结构冗余，简化了决策过程，使产品需求配置更权威、可靠。本文方法为企业MC中的产品需求配置提供了新思路，使企业在维持较低成本的前提下，满足用户的个性化需求，最大限度提升用户满意度。

[1] XU Y N, THOMASSEY S, ZENG X Y. Optimization of garment sizing and cutting order planning in the context of mass customization[J]. The International Journal of Advanced Manufacturing Technology, 2020, 106(7-8): 3485-3503.

[2] KANO N, SERAKU N, TAKAHASHI F, et al. Attractive quality and mustbe quality[J]. Journal of The Japanese Society for Quality Control, 1984, 14(2): 147-156.

[3] 张文召, 吕健, 赵慧亮, 等. 基于R-KANO与G-TOPSIS法的产品设计方案多目标决策方法[J]. 组合机床与自动化加工技术, 2019(7): 146-150. ZHANG W Z, LYU J, ZHAO H L, et al. Multi-objective decision-making model for product design scheme based on R-KANO and G-TOPSIS[J]. Modular Machine Tool ＆ Automatic Manufacturing Technique, 2019(7): 145-150 (in Chinese).

[4] ZHAO S Y, ZHANG Q, PENG Z L, et al. Integrating customer requirements into customized product configuration design based on Kano’s model[J]. Journal of Intelligent Manufacturing, 2020, 31(3): 597-613.

[5] SUH Y, WOO C, KOH J, et al. Analysing the satisfaction of university–industry cooperation efforts based on the Kano model: a Korean case[J]. Technological Forecasting and Social Change, 2019, 148: 119740.

[6] DOU R L, ZHANG Y B, NAN G F. Application of combined Kano model and interactive genetic algorithm for product customization[J]. Journal of Intelligent Manufacturing, 2019, 30(7): 2587-2602.

[7] AVIKAL S, SINGH R, RASHMI R. QFD and Fuzzy Kano model based approach for classification of aesthetic attributes of SUV car profile[J]. Journal of Intelligent Manufacturing, 2020, 31(2): 271-284.

[8] 龙玉玲. 基于Kano模型的个性化需求获取方法研究[D]. 长沙: 中南大学, 2011. LONG Y L. Research on method of acquiring individual demand based on Kano model[D]. Changsha: Central South University, 2011 (in Chinese).

[9] SHAMEEM M, KUMAR R R, NADEEM M, et al. Taxonomical classification of barriers for scaling agile methods in global software development environment using fuzzy analytic hierarchy process[J]. Applied Soft Computing, 2020, 90: 106122.

[10] KUTLU GÜNDOĞDU F, KAHRAMAN C. A novel spherical fuzzy analytic hierarchy process and its renewable energy application[J]. Soft Computing, 2020, 24(6): 4607-4621.

[11] LYU H M, SHEN S L, ZHOU A N, et al.Risk assessment of mega-city infrastructures related to land subsidence using improved trapezoidal FAHP[J]. Science of the Total Environment, 2020, 717: 135310.

[12] GUO S, ZHAO H R. Fuzzy best-worst multi-criteria decision-making method and its applications[J]. Knowledge-Based Systems, 2017, 121: 23-31.

[13] REZAEI J. Best-worst multi-criteria decision-making method[J]. Omega, 2015, 53: 49-57.

[14] VAN LAARHOVEN P J M, PEDRYCZ W. A fuzzy extension of Saaty's priority theory[J]. Fuzzy Sets and Systems, 1983, 11(1-3): 229-241.

[15] 刘大帅, 杨勤, 吕健, 等. 融合用户满意度的用户需求综合重要性研究[J]. 图学学报, 2019, 40(6): 1137-1143. LIU D S, YANG Q, LYU J, et al. Comprehensive importance of integrating user satisfaction with user demand[J]. Journal of Graphics, 2019, 40(6): 1137-1143 (in Chinese).

[16] 王新洲, 舒海翅. 模糊相似矩阵的构造[J]. 吉首大学学报: 自然科学版, 2003, 24(3): 37-41. WANG X Z, SHU H C. Construction of fuzzy similar matrix[J]. Journal of Jishou University: Natural Sciences Edition, 2003, 24(3): 37-41 (in Chinese).

[17] 徐泽水. 三角模糊数互补判断矩阵排序方法研究[J]. 系统工程学报, 2004, 19(1): 85-88. XU Z S. Research on priority method of triangular fuzzy number complementary judgement matrix[J]. Journal of Systems Engineering, 2004, 19(1): 85-88 (in Chinese).

[18] 苏哲斌. 基于一致性逼近的三角模糊数互补判断矩阵的排序方法[J]. 模糊系统与数学, 2009, 23(4): 126-130. SU Z B. The priority method based on consistency approximation for triangular fuzzy complementary judgment matrix[J]. Fuzzy Systems and Mathematics, 2009, 23(4): 126-130 (in Chinese).

[19] CHANG D Y. Applications of the extent analysis method on fuzzy AHP[J]. European Journal of Operational Research, 1996, 95(3): 649-655.

Research on the product demands configuration method based on user satisfaction

ZHANG Di-jing, HOU Zeng-xuan, HUANG Lei, ZHAO You-hang

(School of Mechanical Engineering, Dalian University of Technology, Dalian Liaoning 116024, China)

In order to reasonably determine the preferences and priorities of user demands to adapt to the mass customization production mode and maximize user satisfaction, an improved product user demands configuration method is proposed.The fuzzy clustering analysis method was integrated into the Kano model to classify user demands, the screening was conducted according to their contribution to the improvement of satisfaction,thenthe evaluation factors of customer satisfaction and importance were calculated and a hierarchical structure model of product user demands was established.On this basis, in the fuzzy analytic hierarchy process (FAHP), a fuzzy best-worst method (FBWM) was employed to construct a consistent triangular fuzzy number complementary judgment matrix, the probability concept was introduced to achieve defuzzification and obtain the initial weights of user demands, and the demands evaluation factors served as the correction factors of the initial weights. Then the modified weights were normalized to obtain the comprehensive weights of user demands, thus realizing the configuration of product demands. Taking an enterprise’s eyewear product design and development as an example, the effectiveness of this method was verified, and a user demand configuration strategy was provided for the design and development of eyewear and other products.

user demands; demands configuration; customer satisfaction; Kano model; fuzzy analytic hierarchy process; quantification

TP 391

10.11996/JG.j.2095-302X.2020040649

A

2095-302X(2020)04-0649-09

2020-03-14；

2020-04-26

26 April，2020

14 March，2020；

张迪婧(1995-)，女，河北保定人，硕士研究生。主要研究方向为工业设计、计算机辅助设计、数字化设计。E-mail：shmilyprotea@163.com

ZHANG Di-jing (1995-), female, master student. Her main research interests cover industrial design, computer-aided design, digital design. E-mail：shmilyprotea@163.com

侯增选(1964-)，男，陕西岐山人，教授，博士，博士生导师。主要研究方向为计算机辅助设计技术、虚拟产品开发技术、产品创新设计理论与方法研究。E-mail：hou@dlut.edu.cn

HOU Zeng-xuan (1964-), male, professor, Ph.D. His main research interests cover computer-aided design technology, virtual product development technology, product innovation design theory and method research.E-mail：hou@dlut.edu.cn