基于气象数据的北方试验棚室温度预测模型研究
2020-09-01田芳明李欢朱培培
田芳明,李欢,朱培培
(黑龙江八一农垦大学电气与信息学院,大庆 163319)
现代棚室可以有效调控棚室内部环境因子,创造与外界气候相对可控制的小气候环境。与大田生产相比,能较大程度上满足不同作物在不同季节的生长条件,从而被广泛使用[1-4]。目前在北方的冬季蔬菜生产中,由棚室种植的作物占据主要地位。影响大棚内作物生长发育的主要因素是棚室温度,温度的高低将直接影响产量与品质[5-9]。因此,提高农业大棚温度预测的准确性,不仅可以提前采取相应措施预防突发气象灾害,也可为农技人员制定相应棚室调控方案提供理论依据[10]。
近年来,国内外学者主要应用两大类方法对棚室预测模型进行研究。一是机理方程建模法,用棚室内外能量守恒的思想对棚室温度变化进行建模,研究光辐射、热传导、通风散热等机制对棚内温度的影响,建立棚室温度机理模型[11-17]。Roni Avissar 等[18]以日光棚室为基础,通过研究内外热传导变化趋势,模拟计算热交换系数、热通量等数值,建立小气候热平衡方程较好的模拟棚内气温变化。Wang 等[19]以日然通风的塑料大棚为前提,在地中海气候条件下通过23 d 自然通风试验,建立自然通风下的动态棚室温度模型。李小芳等[20]通过建立棚室能量平衡方程,模拟室内温湿度、棚膜表面的温度变化。霍飞等[21]利用热平衡理论,结合黄瓜生长过程的作物模型,建立了应用于塑料连栋温室的热环境模型。由于从机理的角度考虑棚室温度变化,涉及的影响因子较多,导致所建模型参数多、参数值难以选取、计算难度大,预测效果不理想[22-23]。二是系统辨识方法,主要是根据采集的数据选择输入输出量建立模型。现有研究主要是利用神经网络、支持向量机回归模型等[24-25]。周翔宇等[26]运用经验模态分解方法(EMD)对采集的室外环境因素进行分解,利用改进的深度信念网络(DBN)算法进行多属性特征提取,建立门控循环单元网络对分解的信号特征进行预测并重构出预测结果,进而预测棚室温度。杨雷等[27]将每5 分钟采集的棚外相关因素作为输入,输出为棚内温度。经主成分分析法(PCA)降维,利用粒子群算法(PSO)优化最小二乘支持向量机(LSSVM)的方法,提出了基于PCAPSO-LSSVM 的温度预测模型。王红君等[28]选取棚室内主要的7 个因素,对其进行主成分分析。按贡献率大小依次提取影响日光棚室温度的前3 个成分作为BP 神经网络模型的输入变量,采用贝叶斯正则化算法对三层BP 神经网络优化。建立改进的BP 神经网络棚室温度模型。
多数学者选用外界环境因素作输入,研究外界环境与内部温度之间的关系。鲜有将天气预报的预报信息与棚室内外环境数据结合到模型中的研究。而北方地区的棚室种植一般在秋末到初春期间,由于大气环流季的影响,导致气温多变[29]。天气预报的使用,可以提前预知外界环境的突变,进而可影响棚室内温度的变化。所以,通过构建温度动态模型,找出与试验棚室温度变化有关的因素。设计试验,根据试验棚室内外相关环境变量,引入中国气象网发布的温度预报结论,建立GA-LM-BP 神经网络温度预测模型,实现对北方初春试验棚室温度的准确预测,进一步为棚内温度调控提供参考。
1 棚室温度机理模型
1.1 温度机理模型构建
构建棚室温度机理模型,从机理的角度研究棚室温度变化的原因。模型以内部物质平衡和能量平衡为根据,棚室热量的变化主要通过覆盖层、土壤、太阳的热量、自然通风等进行交换[30]。因此,依据棚室传热和室外气候对棚室内气候的影响程度,选取主要影响棚室内温度变化的因素,构建棚室温度动态平衡关系式。

式中T0为棚室内温度,℃;C0为空气热容量,J·℃-1;Q1为太阳短波辐射热量,W;Q2为通过覆盖材料、围护材料进行的棚室内外空气热交换,W;Q3为棚室内空气与土壤进行的热交换,W;
公式(1)中各项的计算公式如下:

式中ρa为空气密度,在标准条件下(0 ℃,1 个标准大气压);空气密度约为1.29 kg·m-3;Ca为空气恒压比热容,1 000 J/(kg·℃);V0为棚室体积,m3。

式中η 为太阳辐射热量转换系数,无量纲。与棚室所覆盖材料的透射率、太阳照射棚室时室内各组分的吸收率以及作物冠层所吸收的太阳辐射转换为空气热量的转换率等有关;Isolar为外界环境总太阳辐射通量,W/m2;A0为棚室地表面积,m2。

式中K2为棚室覆盖材料与维护材料的热传递系数;T1为棚室外温度,℃;A2为覆盖材料的总面积,m2。

式中K3为棚室表层土壤的热传递系数;T3为土壤温度。

式中Aven为棚室通风时的有效面积,m2;Aw为总通风面积,m2;α 为通风窗开启时的角度。K4为自然通风流密度,m·s-1,其与热压通风和风压通风有关。K4是判断室外风速和通风窗开启与否的函数,表示为:

式中τ、θ、ν 均为通风函数参数,无量纲,与空气流动膨胀、渗透等因素有关;ν 为室外风速,m·s-1;μw为通风窗开启与否,取0 为关闭,1 为开启。
1.2 参数辨识
根据棚室温度动态模型,将模型中的参数分为常量参数和不确定参数。选取2019 年4 月11、12 日数据,采用最小二乘法对模型参数进行辨识,2019 年4 月13、14 日数据验证模型性能,验证后不确定参数辨识值如表1 所示,验证准则见1.3 节。

表1 模型参数辨识结果Table 1 Identification results of model parameter
仿真结果如图1 所示,辨识模型能有效跟踪实际温度,温度模型RMSE 为1.340 7 ℃,Fit 为89.94%。结果表明,棚室温度动态模型可以有效地反映试验棚室温度的变化。
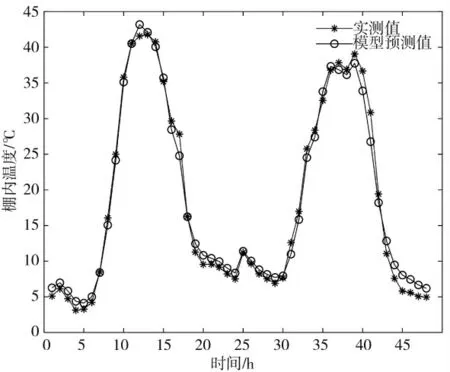
图1 辨识模型预测值与实测值对比Fig.1 Comparison between the predicted and measured values of the identification model
通过构建试验棚室的温度动态模型,确定试验需要采集的环境变量有室内温度、土温,棚外温度、光辐射值和风速。
1.3 模型验证
验证所建立模型的预测效果,采用以下三个指标衡量:均方根误差(RMSE)、模型拟合度(Fit)和决定系数(R2)。对预测值和实测值之间的拟合度进行统计分析,检验模型的性能。若模型性能良好,则RMSE 应尽可能接近0,R2应趋于1,Fit 尽可能达到100%。

式中:yi表示模型输出的模拟值,Yi表示实际试验采集值表示实际试验采集值的平均值,n 表示样本数。
2 材料与方法
2.1 试验设计
试验棚室位于黑龙江八一农垦大学电气与信息学院前楼空地处,坐北朝南,东西走向,长度1.5 m,跨度1 m,高0.75 m。试验时间为2019 年3 月至2019 年4 月。在棚室内布置5 个温度传感器和2 个土壤温度传感器。棚外布置1 个温度传感器、太阳辐射光照计和风速传感器,所用传感器详细参数如表2所示。试验采集系统上位机由Delphi 语言所编写,设置试验采集数据时间间隔为1 min。棚内温度和土壤温度分别取5 个、2 个传感器值的平均数。同时在中国气象网上记录试验期间的天气预报数据。

表2 试验使用的各类仪器Table 2 Various instruments in the test
2.2 LM-BP 神经网络
BP(Back Propagation)神经网络是将信号由输入层传入,通过隐含层到输出层,产生的误差由原路线逐层调整权值,直到模型的输出更接近期望目标[31]。BP 神经网络拓扑结构如图2 所示,其中X1,X2…Xm为输入值,Wij、Wjk为权值,Y1,Y2…Ym为输出值。
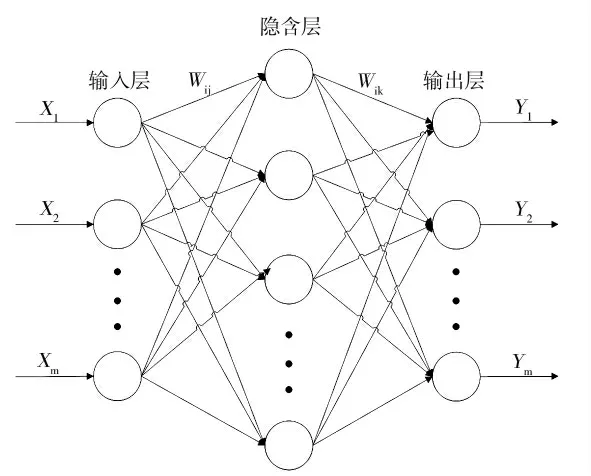
图2 BP 神经网络拓扑结构Fig.2 Topologic pattern of BP neural network
为了加快网络的学习速度、解决“局部极值”问题,使用Levenberg-Marquardt(LM)算法优化网络,LM 算法可以利用自适应调整网络的权值,提升网络的学习速度和泛化能力。
构建LM-BP 神经网络采用的误差函数E(ω)计算公式如(12)所示:

式中:Yj为实际的网络输出向量;zj为期望的网络输出向量;N 为样本数目;ω 为网络权值和阈值所组成的向量。
根据高斯-牛顿法,第j+1 次权值向量ωj+1=ωj+Δω调整为:
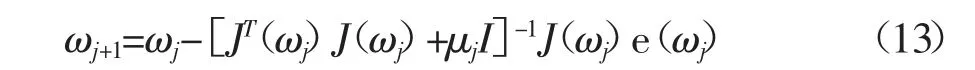
其中,J(ω)为雅各比(Jacobian)矩阵;I 为单位矩阵;μ 为调整值,若Δω使得E(ω)误差值减小,则将μ减小。反之,则增大μ 值。
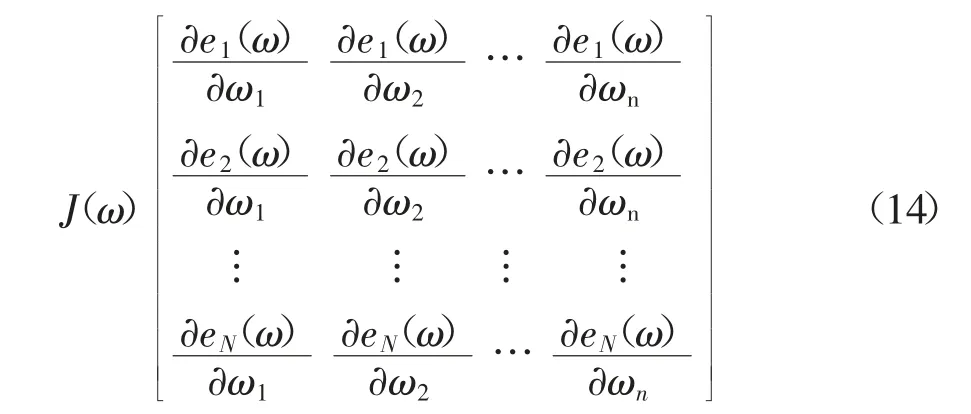
LM 算法的描述如下:
(1)初始化网络的权值和阈值向量ω,令j=0,μ=μ0,并根据试验目的给出误差允许值ε。
(2)计算E(ω),若E(ω)<ε,则转到(5);反之,继续下一步。
(3)根据上述公式(14),计算Jacobian 矩阵J(ω)。
(4)利用公式(13)更新网络权值,并跳转到(2)。
(5)算法结束,保存。
2.3 遗传算法优化LM-BP 网络
遗传算法(Genetic Algorithm,GA)是一个将生物进化原理中的“优胜劣汰,适者生存”思想引入的方法[32]。在一定环境模拟生物进化的方式,根据适应度值选择优等个体进化,不断寻找,从而逼近全局最优解[33]。用GA 算法优化LM-BP 网络,可以增强网络搜寻能力,具体的实现流程如图3 所示。

图3 GA-LM-BP 网络流程图Fig.3 Network flow chart of GA-LM-BP
GA 优化LM-BP 网络的具体实施步骤如下:
(1)种群初始化
个体编码采用二进制编码方法,用{0,1}符号串表示每个个体。二进制和自变量间转换公式为:
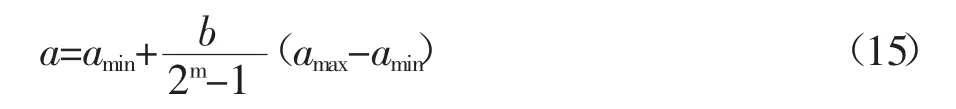
式中:a 是[amax,amin]之间的自变量;b 为m 位的二进制数。其编码、解码操作简单,具有一定并行处理能力。
(2)适应度函数F
该函数是对在空间中的各个个体优良程度的判定。

式中:Yi表示真实值;zi表示网络输出值;m 表示个体数量。F 值越小,表示成为下一代的机会越大。
(3)进行选择、交叉、变异操作
选择操作为了避免基因缺失,提高收敛性,采用随机遍历抽样法。交叉操作选用简单交叉方法组合出新的个体。为了维持物质多样性,变异操作选用随机法。
(4)判断是否完成参数优化
判断网络是否已达到满足的条件(期望误差值、迭代次数),达到要求得到最优的染色体,即最优权、阈值。否则转到(2),继续进行寻找。
(5)构建模型
通过上述步骤找到的最优结果带入LM-BP 网络中,进行模型训练。
(6)验证模型
选择测试数据输入训练好的LM-BP 网络中,预测准确率达到要求则结束。则转到1)重复执行。
3 试验数据预处理
3.1 相关性分析
将所采集的棚室内外数据进行Pearson 相关性

式中:pi为棚内外环境因素;Ti为棚内温度;m 为试验数据个数。r 在0~1 之间,有三个等级<0.4,相关性较弱,0.4≤<0.7;有显著相关性;0.7≤<1,高度线性相关[34]。
由于当环境因子改变时,温度与时间呈指数函数规律。所以设t 为当前时刻,用棚室内t+1 时刻的温度与t 和t-1 时刻的棚室内外环境因素做相关性分析。因为棚外温度的变化影响棚内温度的变化,天气预报所预报的未来温度数据能为棚外温度变化做预判,进而影响温室内温度变化。用天气预报预报的t+1 时刻温度值与t+1 时刻的温室内温度做相关性分析,如表3 所示。结果表明,t+1 时刻的温度取决于t 时刻土壤温度、棚室内外温度、光辐射,t-1 时刻棚内温度、光辐射,以及天气预报预测的t+1 时刻的温度有关。

表3 试验数据相关性分析Table 3 Correlation analysis of test data
3.2 数据归一化
因为试验选用的数据数量级不同,为防止出现数值问题、数据被吞食等现象。对数据采用最大最小法,统一量级,可以加快训练速度,提高模型精度。归一化公式如下:

4 试验结果分析
4.1 LM-BP 模型参数选择
根据试验数据相关性分析,天气预报预报的数据与棚内温度也有较高的相关性。整理数据后,选用2019 年3 月13~17 日每分钟数据进行训练。训练好网络后,再将2019 年3 月18 日的分钟数据选取小时数据做预测。构建以t 时刻棚内外空气温度、土壤温度、太阳辐射与t-1 时刻棚内空气温度、太阳辐射,以及加入天气预报预报t+1 时数据,选用7 个环境参数作为输入,输出为t+1 时刻棚内温度。
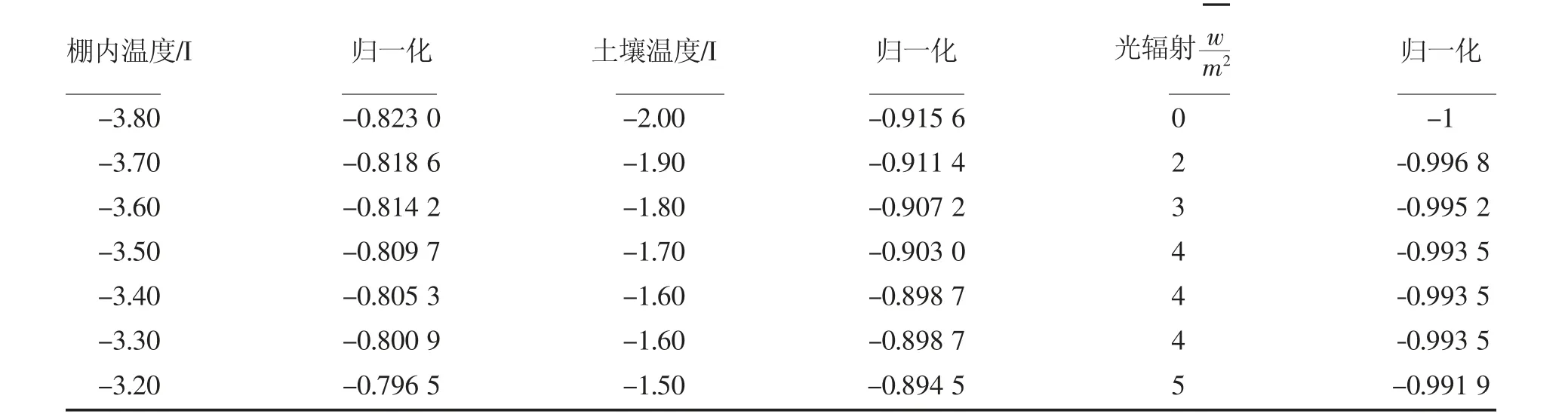
表4 部分归一化后的试验数据Table 4 Test data of partially normalized
虽然隐含层越多,可以提高网络训练精度,但是使得网络复杂化,训练速度也会随之增加,所以结合前人研究,选取3 层网络建立模型。同时,隐含层神经元个数也决定了模型的好坏。数目少难以完成训练,数目多增加迭代次数及训练时间,泛化能力下降致使预测效果下降。根据公式(19)的计算确定隐含层神经元范围。

式中:i 为隐含层神经元的个数,n 为输入层神经元的个数,m 为输出层神经元的个数,a 为常数且1<a<10。通过对不同神经元数的网络进行训练对比,最终确定试验选用的神经网络结构为7-6-1。其他参数如表5 所示。

表5 LM-BP 模型参数选择Table 5 Selection of LM-BP model parameter
4.2 LM-BP 模型预测结果
将训练好的网络保存,代入2019 年3 月18 日整理的数据与同期数据实测值进行验证,验证准则见1.3 节。LM-BP 模型的RMSE 为1.16 ℃,模型拟合度达到91.98%。模型预测每小时温度与真实值的对比如图4 所示。
4.3 GA-LM-BP 模型预测结果
通过上述试验确定LM-BP 神经网络是7-6-1的三层网络结构,并确定GA 相关参数。进化代数设为50,种群规模大小设为40,交叉概率设为0.7,变异概率设为0.01,采用二进制编码,权值和阈值个数如表6 所示。
模型根据GA 算法迭代50 次后找到最优个体,将优选的权、阈值赋值给LM-BP 网络进行训练,再利用测试集对训练好的GA-LM-BP 模型进行验证。模型输出值经过反归一化得到预测值与实际值进行对比,如图5 所示。

图4 LM-BP 模型预测值与真实值对比Fig.4 Comparison of predicted and actual values of LM-BP model

表6 权值和阈值的个数Table 6 Number of weights and thresholds

图5 GA-LM-BP 模型预测值与真实值对比Fig.5 Comparison of predicted and actual values of GA-LM-BP model
使用GA 算法优化的LM-BP 网络在预测结果方面更准确。RMSE=0.88 ℃,Fit 为93.93%,模型拟合度较高,达到了比较理想的结果。表7 为GA-LM-BP 模型预测值与采集实际值的对比。
4.4 模型对比
由上述试验分别建立的LM-BP、GA-LM-BP 模型,其预测效果如表8 所示,可直观的反映出不同模型的性能好坏。其中平均相对误差为:

式中:yi为用不同模型预测得到的温度值;Yi为实际测量值;m 为测试集数量。

表7 GA-LM-BP 模型预测值与真实值的对比Table 7 Comparison of predicted and actual values of the GA-LM-BP model

表8 2 种方法预测效果对比Table 8 Effects of the two prediction methods
由表8 可以得出,利用GA 优化的LM-BP 网络,RMSE 为0.88℃,MSE 为0.77℃,MRE 为9.07%。相比于单纯的使用LM-BP 算法的模型,RMSE、MES 和MRE 分别下降了0.28 ℃、0.57℃和0.44%,模型拟合度提高到93.93%。综合上述分析,GA-LM-BP 网络的预测准确度要更高。
5 结论
研究构建了一个基于气象数据的试验棚室温度预测模型。通过采集、处理试验棚室内外环境变量,分别利用GA-LM-BP、LM-BP 网络算法,将棚室内外环境相关变量和下一时刻天气预报预测数据为输入,预测下一时刻棚内温度变化。通过对比GA-LMBP 神经网络和LM-BP 神经网络所建立的棚室温度预测模型,前者模型预测精度更高,RMSE 为0.88 ℃,模型拟合度达到93.93%。试验表明,利用GA 算法优化LM-BP 网路,可以较准确的预测试验棚室下一时刻棚内温度,缩小了误差,进一步为棚室短期温度预警模型提供理论支持。
利用神经网络算法其预测效果往往比机理建模好,特别是通过优化算法改进后。但是,模型也因为试验地点、时间、环境的不同,不具有普遍代表性。建立的棚室预测模型,只是依托于搭建的试验棚室,对于其他地域的不同棚室还需要通过采集数据重新建模,调试模型参数后达到理想效果。在以后的研究中,还应在提高神经网络算法在棚室温度预测准确度的同时,考虑加入相关执行机构的效果。依据预测温度与作物理想温度之间的差值,提前计算出执行机构相应开闭时间。进一步完善棚室预测模型,使模型更具适用性、推广性。
