火箭橇试验战斗部动态攻角交互式计算与验证*

张晨辉,徐 健

(中国兵器工业试验测试研究院, 陕西华阴 714200)

0 引言

导弹战斗部终点弹道的攻角大小直接影响其侵彻能力,例如,与0°攻角侵彻状态相比,单一动能侵彻战斗部攻角为3°时,侵彻效应降低约5%,当攻角为9°时,侵彻效应降低约8.7%;对于随进侵彻战斗部,初始攻角对其终点效应影响相对更大,当攻角为3°时,侵彻效应降低约7%,当攻角为9°时,侵彻效应降低约30%,理论上撞击靶标时刻攻角越小越有利于侵彻效果[1]。

火箭橇试验是导弹战斗部终点效应考核的一种重要地面动态试验与验证方法,该方法运用高精度专用地面滑轨设施,通过固体火箭发动机实现系统加速,当达到指标速度时,利用战斗部与火箭橇时空分离方式,使战斗部按预定要求的速度和攻角单独侵彻目标,但随着导弹武器系统可靠性指标的不断提高,相关型号研制试验中暴露出过小的控制战斗部初始攻角并不能完全模拟出导弹引战系统的使用极限条件,无法实现对被试导弹武器系统的全面考核,因此,提出了在战斗部着靶时刻必须带有一定攻角的要求。

与导弹空中自由飞行不同,火箭橇试验中战斗部分离后飞行气动力学环境综合了战斗部和火箭橇的马赫数、战斗部姿态、三维相对时空位置、压心突变、局部激波振荡等变化的耦合作用结果,近年来,随着相关研究的推进,在超音速翼型火箭橇气动特性[2]、超音速火箭橇流场气动数值计算分析[3-4]、战斗部攻角对升力系数、阻力系数及升阻比的影响[5]等方面取得了突破性研究成果,但是,在火箭橇试验战斗部动态攻角计算及控制中,需要将复杂的多维空间气动力学插值与战斗部6D飞行姿态计算相结合,相关数学建模、仿真网格划分和耦合求解都十分困难。

针对火箭橇试验中战斗部动态攻角计算和控制难题,结合大量火箭橇试验测试数据,文中采用自编程与CFD数据交换耦合方式,提出了一种交互式的火箭橇战斗部动态攻角工程计算方法,并结合验证试验,对计算精度进行了相关验证。

1 火箭橇运动分析

1.1 控制方程

流体分析时,流体的运动要符合经典力学的3个基本守恒定律,即质量守恒定律、动量守恒定律和能量守恒定律。引入雷诺平均法后控制方程[6]如下:

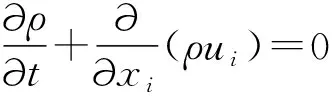
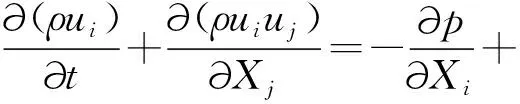
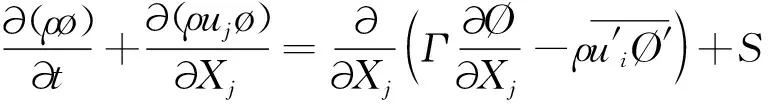
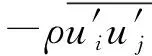
1.2 气动仿真

三维复杂外流场气动仿真是以流体力学与固体力学理论为基础,采用大型计算流体动力学分析软件(CFD)进行模拟,仿真数据为结构气动特性分析提供基础。

现阶段国内外物体外流场的数值仿真研究中,通常应用N-S方程耦合双方程湍流模型对湍流现象进行模拟,而在双方程湍流模型中基于k-ω模型的SST(剪切应力输运)湍流模型[7]以其优势得到广泛应用:①该模型能适应压力梯度变化的各种物理现象;②该模型中可应用粘性内层,可精确模拟边界层的现象,无需使用较容易失真的粘性衰减函数。研究表明,采用SST模型进行外流场湍流模拟结果与风洞试验结果基本吻合,故采用SST模型对中文火箭橇复杂外流场问题进行研究。

1.3 运动计算基本原理

龙格-库塔(Runge-Kutta)方法[8-9]是用于非线性常微分方程解的重要的一种隐式或显式迭代法,该方法有如下优点:1)具有同一型式的计算流程图;2)不需要进行“起始”计算;3)在计算过程中很容易改变步长;4)能很好的适应方程右端为间断函数的情况。四阶龙格-库塔法的截断误差为O(h5)。程序框图如图1所示。

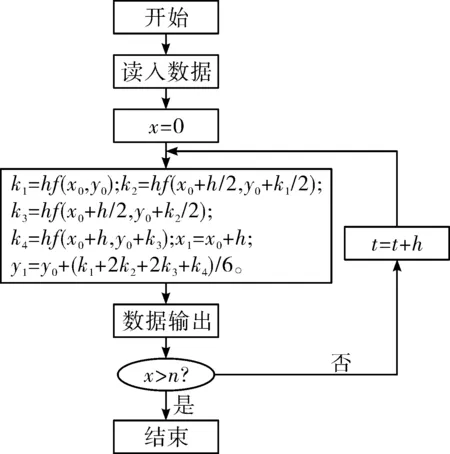
图1 计算流程图

2 战斗部动态攻角交互式计算方法

2.1 气动力学环境分析

根据弹橇分离后战斗部的速度、姿态、时空位置和局部激波等因素,分析战斗部飞行过程的气动力学环境变化,得出战斗部气动阻力、升力和力矩曲线。

利用流体软件ANSYS CFX进行火箭橇流场计算,合理设置边界条件。火箭橇模型表面采用无滑移的固壁边界条件,滑轨及地面采用滑移边界条件,采用SST(剪切应力输运)湍流模型,采用非结构网格求解可压缩雷诺平均N-S方程对火箭橇复杂外流场问题进行计算。

2.2 耦合交换数值计算

结合流体软件ANSYS CFX和基于四阶龙格-库塔插值与牛顿运动定律的VB自编程序,建立战斗部攻角计算方法,形成了更为科学的计算理论。

1)结合导弹引战系统终点效应火箭橇试验气动力学环境分析与计算,进行数学建模,弹橇分离点与目标距离段的弹道数学模型的坐标轴为：选取弹橇分离时刻弹的质心位置为坐标原点,水平轴ox轴与滑轨平行,选取火箭橇飞行方向为正;沿直轴oy在弹纵向对称面内与水平轴ox相垂直,向上为正;oz轴垂直于oxy面,翻转力矩以使被试品系统抬头的力矩为正,以使被试品低头的力矩为负,该坐标轴的建立基于实际的火箭橇试验要求。初始求解程序数学模型如式(1)所示。

(1)

式中：m为战斗部质量(kg);vx为航向速度(m/s);vy为纵向速度(m/s);ξ为战斗部攻角角速度(rad/s);x为航向位移(m);y为纵向位移(m);α为攻角(rad);Jz为战斗部赤道转动惯量(kg·m2);F为航向空气阻力合力(N);S为纵向空气阻力合力(N);M为翻转力矩(N·m)。

2)为了仿真计算火箭橇在滑轨上的运动过程,得到火箭橇系统各部件运动轨迹,根据火箭橇结构参数建立火箭橇运动模型,用VB语言编程,运用四阶龙格-库塔对控制方程求解,进行初始化求解程序编制。

3)在初始化计算的基础上,与气动分析前处理软件ICEM进行战斗部分离后飞行气动力变换数据。

4)同时进行网格再划分CFD分析及后处理等,通过多次迭代计算,得出火箭橇试验战斗部弹橇分离后飞行姿态与攻角变化。

此方法已多次应用于火箭橇试验战斗部攻角控制中,并得到充分验证。

3 计算方法分类

根据计算与建模的不同,对上述动态气动力学环境数值计算方法进行分类,并阐述其特点及适用范围。

1)一次初算多点插值方法

利用ANSYS CFX对起始点气动力学环境进行分析,得到起始点战斗部及橇体阻力/升力、战斗部翻转力矩等初始参数,通过VB攻角计算程序,推算出弹橇分离过程中每点战斗部速度、攻角、航向飞行距离、角速度、橇体倾斜角度、航-纵向拉开距离等参数,据此以一定的距离间隔构建多个点的力学模型,分别对各力学模型进行气动特性分析,得到各间隔点战斗部及橇体力学参数,进行VB自编程与CFD数据交换耦合计算求解得到战斗部攻角变化曲线。

此方法依据一次初算结果,构建多间隔点的数值模型,可并行计算,但战斗部飞行距离长的情况下角速度的累积偏差导致各插值点的攻角将出现较大偏差,故计算时间短、精度较差,适合于转动惯量较大或飞行距离较短的战斗部攻角估算,在工程计算中应用较为广泛。

2)分段逐步外推方法

同理,先计算出弹橇分离起始点初始参数,结合弹橇分离点与靶标距离段的弹道模型,将该段距离均分N段,利用VB自编程推算在该气动力环境下运行至第1段段末位置时战斗部攻角等参数,同样建模计算出第1段段末位置参数,利用四阶龙格-库塔插值进行外推,得出第2段段末位置参数,以此类推,得到各位置战斗部攻角等参数。

此方法需要分段计算,需多次建模、多次插值计算,但这种方法推导出的每位置点攻角等参数更准确,故计算时间较长、精度较高,适合于转动惯量较小且精度要求高的战斗部攻角计算,耗时长,不适合于工程计算。

3)区间插值方法

此方法是第一种方法的演变,针对飞行距离较长情况将其分为2个或3个短距离的区间,在区间内采用一次初算多点插值方法,将上一区间末的输出结果作为下一区间的输入结果,最终获取战斗部攻角的变化趋势。

此方法对第一种方法进行了优化,第二区间或第三区间战斗部的攻角模拟更加准确,故计算时间较短、精度较高,适合于转动惯量较小或飞行距离较长的战斗部攻角计算。

4 火箭橇试验验证

下面通过火箭橇试验案例对3种计算方法特点及适用性进行分析,战斗部由模拟件代替,橇体进行了局部简化处理,建立模拟件火箭橇仿真物理模型,假设模拟件转动惯量及飞行距离等参数。

案例一:火箭橇结构外形如图2所示,模拟件以预置攻角0°安装在橇体上,假定弹橇分离速度300 m/s,模拟件质量500 kg,火箭橇橇体质量600 kg,模拟件质心1 400 mm(距后端),模拟件转动惯量200 kg·m2,空气密度1.067 kg/m3,飞行距离设定为30 m。

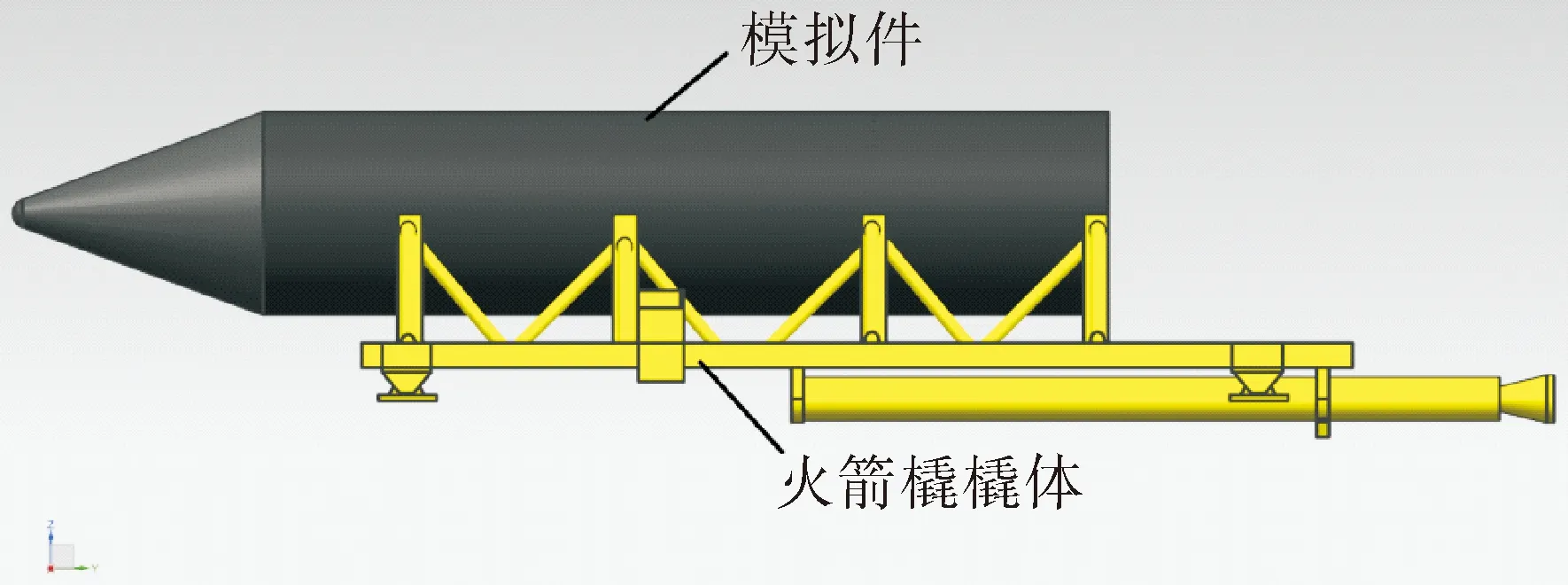
图2 火箭橇结构外形图

下面分别采用一次初算多点插值方法及区间插值方法,获得模拟件的攻角变化。特征位置模拟件及橇体表面压力云图如图3所示。

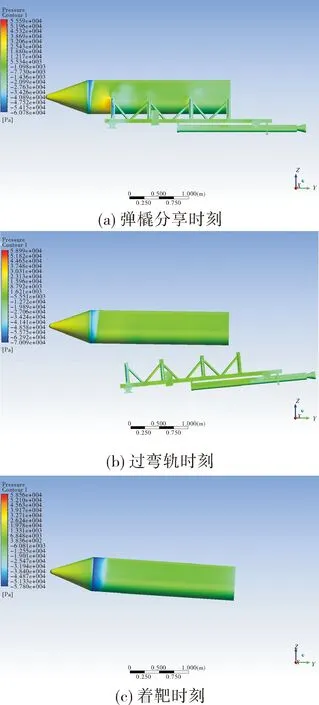
图3 模拟件及橇体表面压力云图

如图4所示,采用一次初算多点插值方法及区间插值方法计算得出着靶攻角分别为4.055°、3.774°,根据大量的试验测试数据进行反演推算,实际试验中着靶攻角为3.5°。区间插值法将30 m飞行距离分为12 m和18 m两个区间,在第一区间,攻角变化趋势与一次初算多点插值方法一致,在第二区间,由于区间插值法获取的模拟件各时刻的攻角较为准确,攻角发散程度较小,计算精度较高,计算偏差为0.281°,计算时间增加一倍。由于案例中模拟件转动惯量较大,两种方法同一时刻模拟件攻角偏差不会引起较大的翻转力矩差异,故区间插值方法优势不明显;若飞行距离缩短为20 m,两者偏差会更小,仅为0.03°。因此,区间插值法适合于转动惯量较小或飞行距离较长的攻角计算,反之,采用一次初算多点插值方法可以更快捷地得出攻角变化趋势。

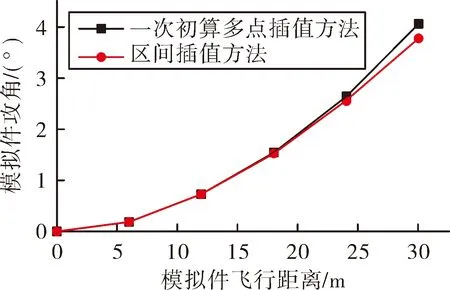
图4 两种方法攻角变化趋势对比

案例二:上述参数不变的情况下,为对比一次初算多点插值方法及分段逐步外推方法,假定模拟件转动惯量为100 kg·m2,获得两种情况下模拟件的攻角变化趋势,如图5所示。

图5 两种方法攻角变化趋势对比

如图5所示,由一次初算多点插值方法及区间插值方法计算得出的着靶攻角分别为7.275°和5.647°,根据大量的试验测试数据进行反演推算,实际试验中着靶攻角为4.9°。由于分段逐步外推方法能够精确模拟出各时刻力学参数,计算精度提高了22%,但由于计算中进行了5次分段计算,故计算时间增加5倍,不适用于工程计算。对于模拟件飞行距离短的情况,譬如假定飞行距离20 m,计算方法引起的偏差不会太大,计算偏差仅为0.64°。

5 结论

1)文中针对火箭橇试验中战斗部攻角控制,开发了一种基于气动环境分析的耦合交换数值计算手段,解决了火箭橇战斗部动态攻角工程计算难题。

2)文中对计算方法分类、特点及适用范围进行介绍,并通过火箭橇试验案例分析其计算精度及计算时间,一次初算多点插值方法计算时间短、精度较差,适合于转动惯量较大或飞行距离较短的战斗部攻角估算,在工程计算中应用较为广泛;分段逐步外推方法计算时间较长、精度较高,适合于转动惯量较小且精度要求高的战斗部攻角计算,但耗时长,不适合于工程计算;区间插值方法计算时间较短、精度较高,适合于转动惯量较小或飞行距离较长的战斗部攻角计算。该研究结果可用于精确、高效战斗部火箭橇试验攻角设计与控制。