高超声速飞行器鲁棒纵向控制技术研究*

张健松,马清华,黎海青,范黎明

(1 西安现代控制技术研究所, 西安 710065; 2 北京航空航天大学, 北京 100191)

0 引言

高超声速飞行器具有速度快、航程远和机动性强等特点,有着巨大的军事和民用价值,目前成为了各国的重点研究对象[1]。

高超声速飞行器的纵向模型存在强非线性和耦合、多种不确定性和大气扰动等控制难点[2]。首先,高超声速飞行器的纵向模型是高度非线性和耦合的;其次,在高速飞行过程中飞行状态及气流扰动会使其气动参数发生变化,这导致了参数存在不确定性;第三,在大机动飞行时,可能激发出一些未建模的动态,同时舵和传感器自身误差也将导致未建模不确定性;最后,飞行器的速度越快,对扰动的响应越快,容易受到大气干扰的影响。以上这些因素都对飞行性能产生影响,其鲁棒闭环控制系统的设计具有挑战。

过去20年中,一些学者致力于实现高超声速飞行器的鲁棒飞行。文献[3]提出了一种基于近似反馈线性化技术的非线性控制器,实现了高度和速度通道的控制。文献[4]提出了一种保性能方法用于解决模型中存在的非线性和耦合问题。但是,上述研究没有讨论不确定性对飞行器闭环控制系统的影响。文献[5]设计了一种干扰观测器用于抑制参数摄动和外界扰动的影响,但这种方法需要保证总干扰的变化率是有界的。文献[6]提出了一种定阶H∞控制方法来减弱模型不确定性的影响,但H∞控制方法无法在全频段内抑制干扰的影响。

针对高超声速飞行器鲁棒纵向控制问题,文中提出一种基于信号补偿的鲁棒控制方法,所设计的控制器由状态反馈控制器和干扰补偿器两部分构成,其中状态反馈控制器实现飞行器期望的控制性能,然后将非线性和耦合、未建模动态、参数不确定性和外界大气扰动等视为同效干扰,通过引入干扰补偿器来抑制同效干扰的影响。通过飞行器纵向闭环控制系统仿真,验证了所提出鲁棒控制器的有效性。

1 高超声速飞行器控制问题建模

文中研究的高超声速飞行器纵向模型为美国NASA研发的锥体加速器模型(见图1)。

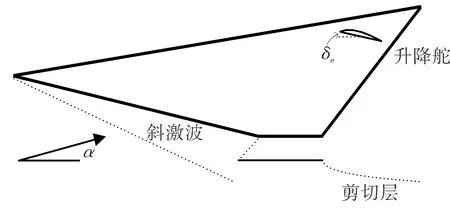
图1 高超声速飞行器锥体加速器模型

该模型分为高度和速度两个通道,可由如下的非线性方程描述[7]:

(1)

式中:速度V、高度H、航迹角γ、攻角α和俯仰角速度q是系统状态量；m和Iq分别为飞行器的质量和转动惯量；g表示重力加速度常数；di(i=1,2,…,5)为时变的外界扰动；推力T、升力L、阻力D和俯仰力矩My可由式(2)表示。

(2)

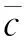
(3)

式中：δe表示舵偏角；λCi(i=1,2,…,7)为参数不确定性,表示气动参数的理论值与实际值之间的偏差。发动机的模型可由式(4)描述。

(4)

式中：βc为节流阀开度;ξn和ωn分别表示系统的阻尼和频率;λC8为未建模不确定性,表示理论模型和实际模型之间的偏差部分。如果忽略大气扰动di(i=1,2,…,5)和不确定性λCi(i=1,2,…,8),那么可以将式(1)～式(4)所描述的模型称为名义非线性模型。

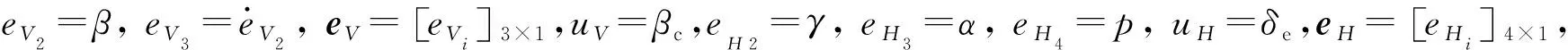
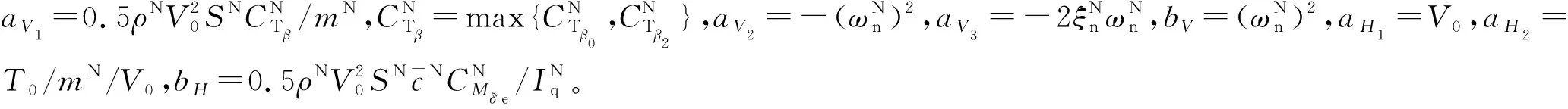
(5)

式中：ΔV=[ΔVi]3×1和ΔH=[ΔHi]4×1是同效干扰,包含非线性和耦合动态、参数不确定性、未建模不确定性和外部大气扰动。

2 鲁棒纵向控制器设计

从式(5)可以看出,实际模型可以看作含有同效干扰的名义模型。因此,文中所设计的鲁棒纵向控制器由两部分构成:状态反馈控制器用于实现名义模型期望的跟踪性能,干扰补偿器用于减弱同效干扰对整个系统的影响。

控制输入uj由下式表示:

uj=uNj+uRj

(6)

式中：uNj表示状态反馈控制输入;uRj表示干扰补偿控制输入。

对于式(5)所描述的实际系统,通过忽略同效干扰Δj(j=V,H),可以得到名义模型。针对名义模型,基于状态反馈控制方法构造状态反馈控制器,具体形式如式(7)。

uNj(t)=Kjej(t)

(7)

式中：Kj表示状态反馈控制增益矩阵。根据式(5)～式(7)可以得到:

(8)

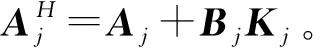
然后,引入干扰补偿输入uRj来抑制同效干扰Δj的影响:

uRj(s)=-Dj(s)Δj(s)

(9)

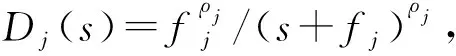
然而,无法直接测得Δj的值,所以需重构干扰补偿输入。设Gj(s)为系统的传递函数,由式(8)可知,Gj(s)的具体形式如下:

(10)

由式(8)可以得到系统的输入uRj(s)和输出yj(s)之间的关系式如式(11)。

(11)

忽略初始状态Ej(0),上式可得:

(12)

合并式(9)和式(12)可得:

(13)

那么,最终的控制输入uj(s)可以由式(14)给出。

(14)

整个闭环控制系统的框图如图2所示。

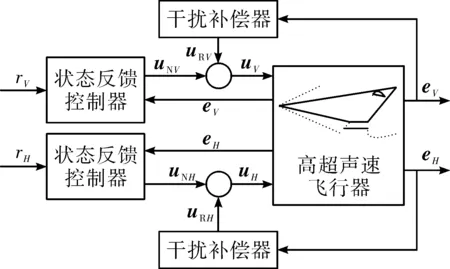
图2 高超声速飞行器闭环控制系统框图

3 数字仿真

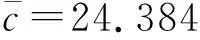
攻角和节流阀开度的初始值为α0=1.790°和β0=0.176 2°。飞行任务:飞行速度和高度由15 060 ft/s和110 000 ft同时分别提升到15 160 ft/s和112 000 ft(1ft=0.304 8 m)。仿真结果如图3～图5所示。图3为速度和高度响应图,从图中可以看出,速度和高度可以很好的跟踪所给出的参考指令信号,速度和高度的最大稳态误差分别为0.3 ft/s和0.4 ft。图4和图5分别为系统其它状态量(航迹角、攻角和俯仰角速度)和控制输入(节流阀开度和舵偏角)的响应图。可见,在存在强非线性和耦合、参数和未建模不确定性以及外界大气干扰的情况下,文中所设计的鲁棒控制器可以实现较好的跟踪效果。

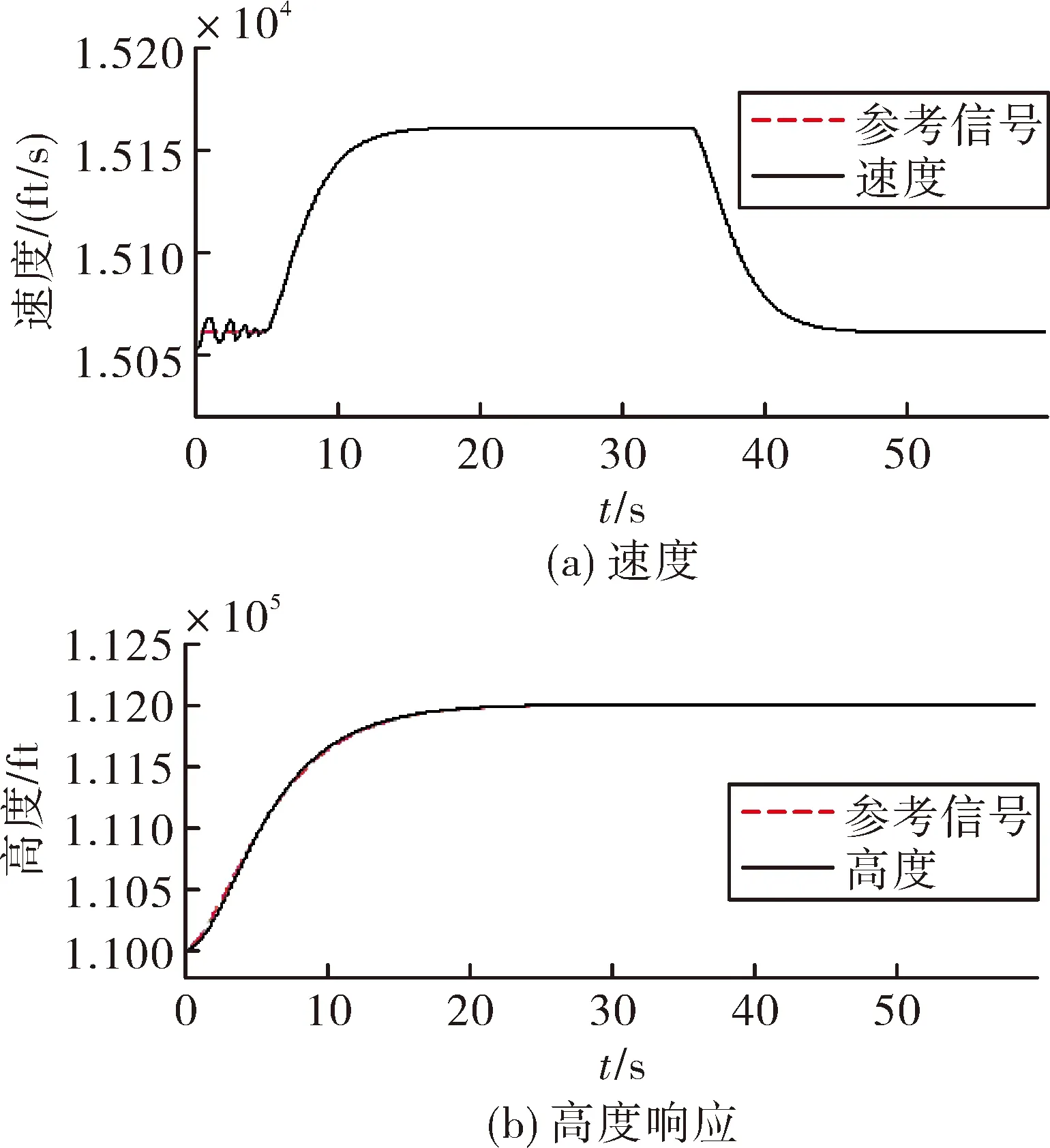
图3 速度和高度响应图

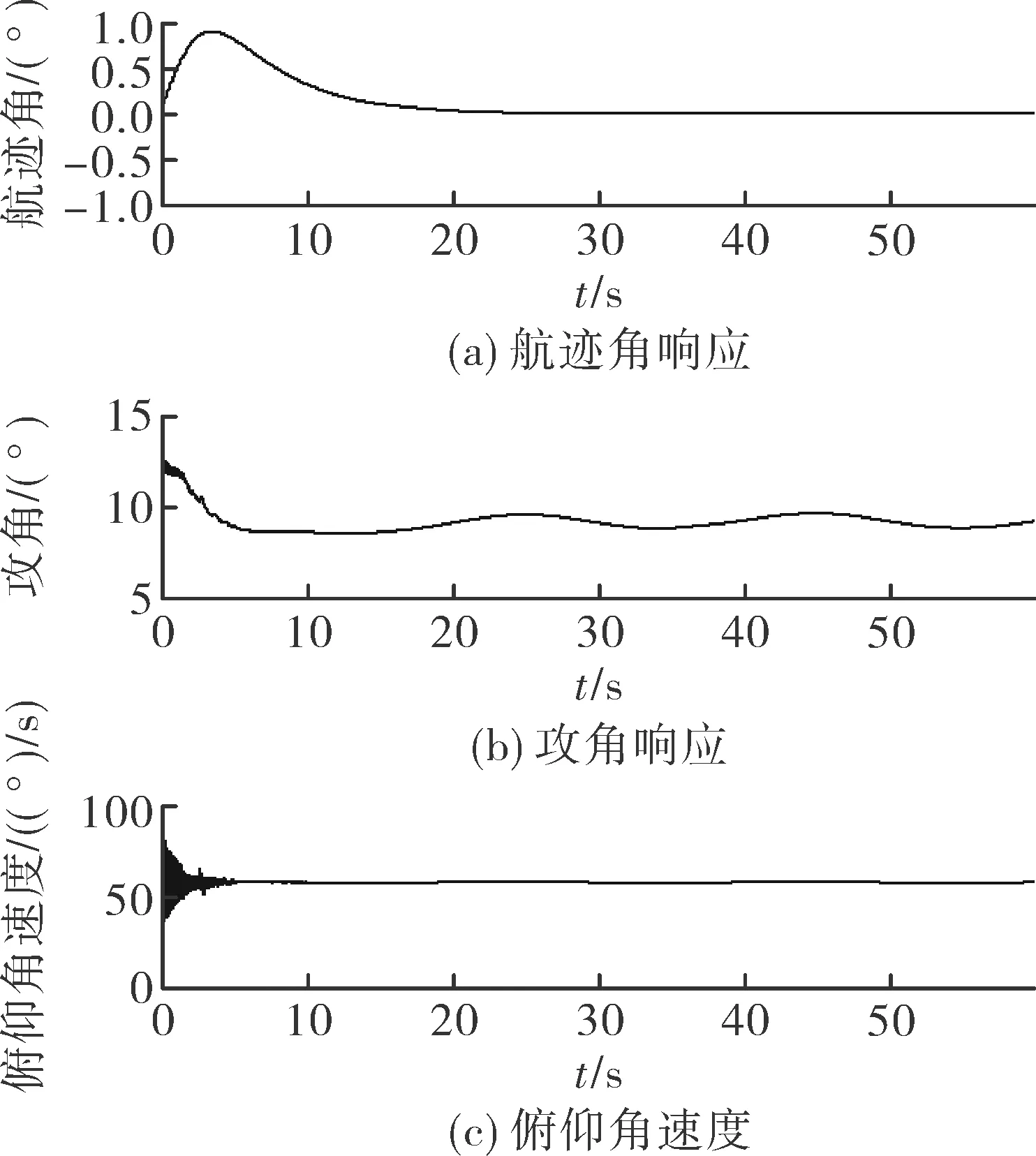
图4 航迹角、攻角和俯仰角速度响应图

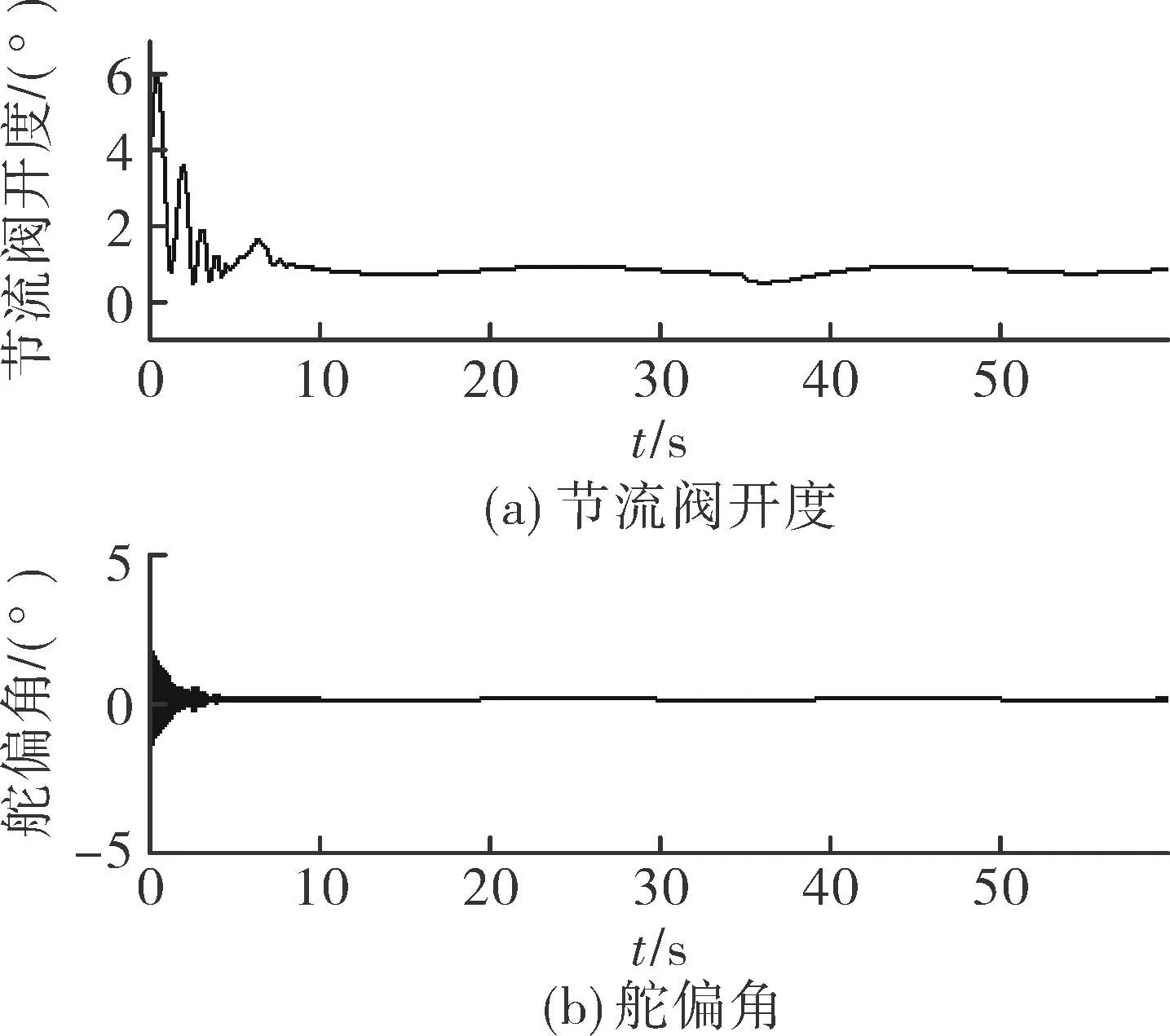
图5 节流阀开度和舵偏角响应图

将干扰补偿器参数设置为fV=0和fH=0,这样控制器就变成单纯的反馈线性化控制器,其控制结果如图6所示。可见,单纯由反馈线性化控制器组成的闭环控制系统存在明显的跟踪误差。由图3和图6对比可知,文中所设计的鲁棒控制器跟踪效果更好,因为非线性和耦合、多种不确定性和外界干扰可以通过干扰补偿器得到抑制。

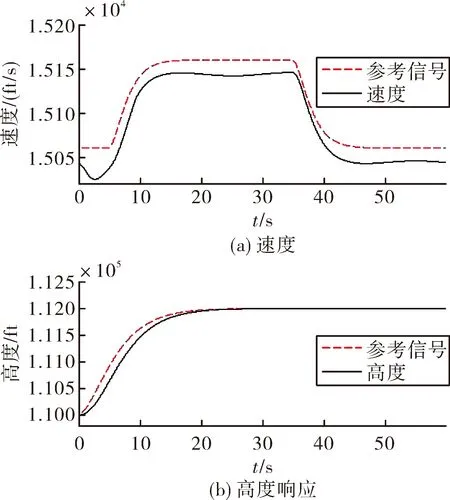
图6 不含干扰补偿的高度和速度响应图

4 结论

文中针对具有强非线性和耦合的高超声速飞行器,考虑了参数不确定性、未建模不确定性和外部大气干扰影响,提出了一种鲁棒纵向控制器。该控制器由状态反馈控制器和干扰补偿器两部分组成。通过高超声速飞行器闭环控制系统仿真实验,与单纯的状态反馈控制器相比,仿真结果证明了中文所提出鲁棒控制方法的优越性。