梯形加减速算法在MCU控制步进电机中的应用研究

摘要：为了实现单片机对步进电机的精准控制，通过研究梯形加减速运动数学模型分析电机机械运动特性，建立了速度与脉冲、加减速度的数学关系，在STM32单片机中实现了梯形加减速算法的转换。经调试，步进电机在MCU控制下运行平滑稳定，响应灵敏，不存在失步、过冲现象。

关键词：梯形算法;数学模型;步进电机;MCU

0    引言

随着企业的转型升级，智能化设备备受企业青睐，由于步进电机无需反馈就能对位置和速度进行精准控制，故其在工业自动化设备中应用极为广泛。但在一些速度变化较大、加减速频繁的设备中，步进电机时常发生失步、过冲等现象，导致控制失灵、精度不高等问题。本文对上述问题进行研究，发现通过梯形加减速算法控制步进电机，具有运行稳定、响应灵敏的优点，不存在失步、过冲等现象。

1    MCU控制步进电机硬件系统

如图1所示，MCU控制步进电机硬件系统以STM32F103单片机为核心，硬件系统包含了四大部分：一是串口触摸屏，主要用于用户输入步进电机运行步数、加速度、减速度、最高运行速度等数据，并提供控制步进电机前进、后退和急停的按钮;二是步进电机驱动部分，该部分主要由四线制57H2P7842A4步进电机和DM542驱动器组成，用于驱动负载的滚珠丝杆滑台在直线导轨上按规定的速度稳定、平滑地往返运动;三是复位检测传感器，系统启动时根据传感器位置信号使滚珠丝杆滑台复位;四是电源部分，该电源主要为负载提供3.3 V、5 V、24 V直流电压。

2    梯形加减速运动数学模型

步进电机梯形加减速运动数学模型如图2所示，模型曲线以角速度ω、时间t分别为纵轴和横轴，曲线有恒加速、匀速和恒减速三个阶段，涉及最高速度SPD、电机运行步数L、加速度A和减速度D四个参数。通过研究模型曲线分析电机角速度ω、加减速度？覣、脉冲信号周期δt、脉冲数n等参数的数学关系，使步进电机在MCU控制下按照梯形曲线做平滑稳定的机械运动，避免发生失步和过冲现象。

2.1    MCU定时器值与电机加减速度数学关系

通常，步进电机运转速度的大小取决于其输入数字脉冲信号频率的高低，脉冲频率越高速度越快，与周期长短的关系则反之。

因此，MCU根据Cn与加减速度、步进电机步距角、脉冲数n以及定时计数器的计数频率的数学关系自动生成定时计数器的计数值，从而输出第n步步进电机所需相应频率的脉冲。

2.2    电机加减速度？覣与脉冲数

从图2（a）可知，步进电机运动梯形曲线有4个变化阶段：一是从零开始加速;二是恒加速到匀速;三是匀速到恒减速;四是减速至停止，如使步进电机按照曲线轨迹运动，除控制好脉冲频率之外，还要掌握其加减速度变化时刻的规律。

3    算法在MCU中的实现

根据梯形曲线数学模型（图2），步进电机运动状态可分为停止、加速、匀速和减速4种状态，其中开始和停止时刻可统称为停止状态。

4    安装与调试

4.1    硬件安装

硬件安装主要包括三大部分，一是串口触摸屏模块，二是电机驱动器模块，三是位置传感器模块。

串口触摸屏通过串行方式与STM32单片机通信，具有编程简单、操作方便等优点，安装时只需要接通DC5 V电源和两机通信线TX、RX即可。步进电机控制系统触摸屏主控界面主要有步進电机运行总步数、最高速度、加速度、减速度4个输入参数窗口，其中速度单位为rad/sec，加减速度单位为rad/sec2;界面中还有电机前进、后退和急停3个控制按钮。

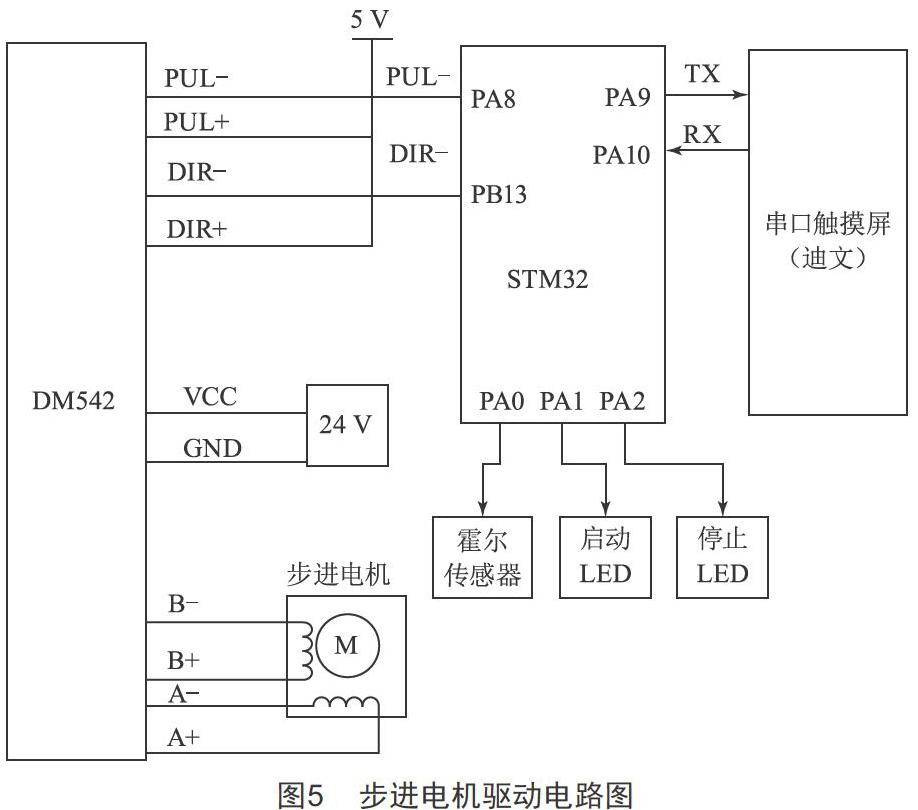
步进电机驱动电路如图5所示，电机驱动器采用共阳极接法，工作电源为DC24 V，信号端电源为DC5 V，脉冲信号输入端PUL-和方向控制端DIR-分别接至STM32F103单片机的定时计数器脉冲输出端PA8和PB13端口。

步进电机复位检测采用了霍尔传感器，当MCU系统开机时自动检测滚珠丝杆滑台是否在原点，如不在原点则自动复位。调试过程中使滚珠丝杆滑台偏离原点，开机观察能否自动复位。

4.2    调试与分析

调试前把电机驱动器的细分数设为32，即6 400步/转，步进电机电流设置对应为2.8 A，然后在步进电机控制系统主控界面输入不同的运行步数、最高运行速度、加速度和减速度值，在调试过程中，可借助电机启动或停止同步状态指示灯观察步进电机有无失步、过冲等现象，如依序输入12 800（6 400×2）、1 200、600、600，点击“前进”按钮，同时会观察到启动指示灯快速闪烁1次，这时电机将按照设定参数做加减速运动，电机转动2圈后停止，停止同步状态指示灯快速闪烁2次。经输入不同值进行调试，发现步进电机运行过程平滑稳定，没有发生失步和过冲等现象，梯形加减速算法在MCU控制步进电机中起到了关键作用。

5    结语

用户给定运行步数、最高运行速度和加减速度的前提下，在MCU控制步进电机中植入梯形加减速算法后，经测试，步进电机运行平滑稳定、响应灵敏，避免了在启动或停止时发生失步或过冲等现象。

[参考文献]

[1] 汤建文，王仁波，王海涛.基于FPGA的数字多道梯形成形算法研究[J].测试技术学报，2018（5）：405-410.

[2] 肖利哲，王学娟.基于变步长梯形算法GM（1，1）模型背景值的优化[J].统计与决策，2016（23）：8-11.

[3] MADNI A M，VUONG J B，YANG D C H，etal.A Differential Capacitive Torque Sensor With Optimal Kinematic Linearity[J].IEEE Sensors Journal，2007，7（5）：800-807.

[4] 宋玉宏，周定艺，詹金远，等.基于STM32单片机的电机驱动设计[J].顺德职业技术学院学报，2018（2）：6-9.

收稿日期：2020-04-29

作者简介：刘俊侃（1971—），男，广东东源人，讲师，研究方向：机电一体化。