基于LMS-自适应滤波算法的经验模态分解故障诊断方法研究

李杨 刘桂秋 张志锋

摘要：对于多相电机定子绕组或逆变桥开关管开路造成的故障，其故障信号常被电机噪声和环境噪声所淹没。现提出一种将LMS-自适应滤波算法和经验模态分解（EMD）结合的特征信号提取方法，通过自适应滤波算法滤除含有噪声污染的故障信号中电机产生的电磁噪声，再对滤波后的信号进行经验模态分解，并提取出故障特征信号。仿真实验表明，该方法能够有效消除电机电磁噪声的干扰，计算快且简单易行，具有良好的可操作性。

关键词：LMS-自适应滤波算法;EMD;故障诊断;电机噪声

0    引言

在常用的非平稳信号分析方法中，Huang等提出的经验模态分解（EMD）非常适用于处理非线性、非平稳信号[1]，该方法将任意信号分解为若干个基本模式分量（IMF），这些IMF可以较好地反映信号的时频特性。但在实际应用中，由于输入信号部分缺失、受噪声影响或受其他脉冲信号的干扰，在EMD分解过程中会产生模态混叠[2-4]问题，而选择合适的滤波方法滤除原信号中的干扰信号可以有效解决此问题。

LMS-自适应滤波算法可以直接利用观测数据，根据设定的目标信号不断递归更新处理参数。这样的处理方法不但更接近实际情况，而且更符合非平稳信号的滤波需求，因而其在许多参考文献中都在去噪方面有广泛应用[5-7]。本文选用LMS-

自适应滤波算法与经验模态分解相结合的方法，解决非平稳信号的特征信号处理问题。

1    LMS-自适应滤波算法

自适应滤波是近些年发展起来的一种滤波方法，其由于具有更强的适应性和更优的滤波性能，在不同领域得到了广泛的应用。本文选用收敛速度快且易行的LMS-自适应滤波算法来去除电机的振动噪声。

采用LMS-自适应滤波算法的目的是使滤波后的实际输出值和期望输出值之间的均方误差（MSE）最小，其均方误差为：

当均方误差最小时有：

所以在最小均方误差意义下的最佳FIR横向滤波权向量为：

应用最速下降法得到：

2    EMD信号处理方法

经验模态分解（EMD）方法是黄锷博士提出的一种自适应信号处理方法，特别适用于非线性、非平稳信号的特征量提取，该信号处理方法关键是经验模式分解过程，把复杂信号分解为有限个本征模函数（IMF），分解出的每个IMF分量包含了原信号不同时间尺度的局部特征信号。EMD分解的具体步骤可以描述为：

（1）需求解出原信号x（t）的极大值和极小值点，若信号无极值点则先对其微分，再对得到的结果进行积分来求取极值点。根据极值点用三次样条插值法求取信号上下包络线，上下包络线均值曲线记作m1（t）。将原信号x（t）减去包络线均值曲线m1（t），得到一个新信号序列h1（t）。如果h1（t）不满足IMF条件，把h1（t）作为原信号重复上述步骤，直到其平均包络线趋于零，则hk（t）为第一个IMF分量，记作c1（t）。

（2）将原信号x（t）减去第一个IMF分量c1（t）得到新信号序列，对新信号重复步骤（1）可得到多个IMF分量cn（t）和一个不可分解的余项rn（t）。因此，原信号x（t）可看作是多个IMF分量cn（t）之和加上余项rn（t）信号的和。

EMD分解的本质是对信号的筛分过程，将原信号从高频到低频依次分解出不同频率段的信号分量。但由于电机在运行时受机械振动噪声、空气动力振动噪声和电磁振动噪声等多个噪声源的影响，EMD在分解故障信号过程中会产生模态混叠问题，即不同频率段信号混叠在一个IMF分量中，对故障信号提取造成干扰。由文献[8]可知电机由逆变器供电时电机的振动噪声源特征频率，因此可采用自适应滤波算法先对原信号进行滤波处理，滤除电机振动噪声源的干扰信号，再进行EMD分解，可以很好地解决模态混叠问题，提取出故障信号。

3    仿真分析

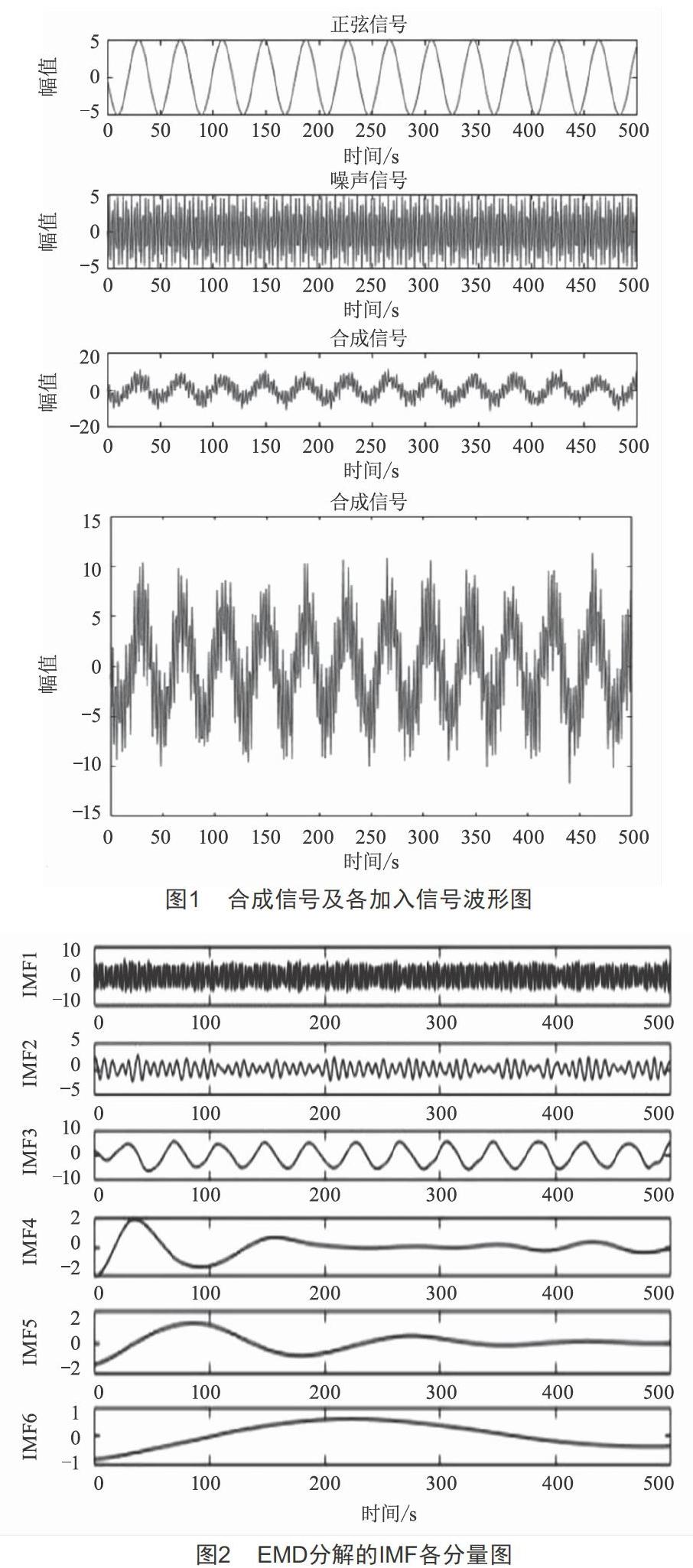
为了验证本文方法的可操作性，在Matlab中进行仿真分析。选用模拟噪声污染的故障信号x（t），x（t）由频率为50 Hz的正弦信号x1（t）、模拟故障的周期性指数衰减信号x2（t）、频率为正弦信号1.5倍的噪声信号x3（t）组成，具体为：x1（t）=

5sin（100πt）、x2（t）=e-50tsin（1 000πt）、x3（t）=10sin（1 500πt）。圖1为没有污染的正弦波信号x1（t）波形图、加入的噪声x3（t）的波形图及未经过滤波处理的输入合成信号x（t）的波形图，图2为EMD分解出的各IMF分量图。

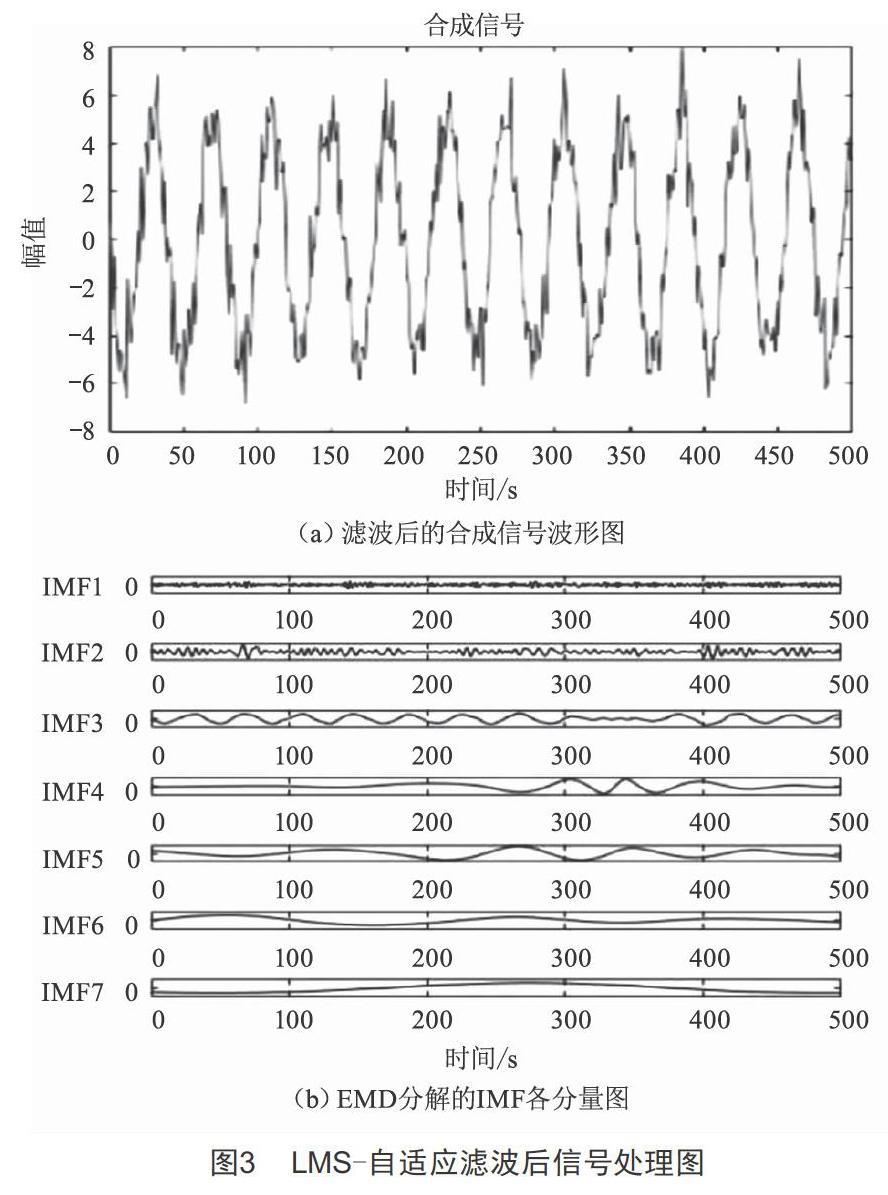
把原故障信号x（t）通过LMS-自适应滤波算法滤除噪声干扰项x3（t），滤波过程的目标函数为正弦信号x1（t），滤波之后得到的输入波形如图3（a）所示，图3（b）为滤波后的信号经过EMD分解出的IMF分量图。

将图1中的合成信号与图3（a）中滤波后的合成信号进行对比可以看出，经过LMS-自适应滤波之后的信号更圆滑，更接近目标信号，并且EMD分解出的IMF更加细致。图3（b）和图2相比EMD多分解出一个IMF分量，使得分解出的每一个IMF频率段更加清晰准确。

4    结语

针对含有电机振动噪声干扰的故障信号提取问题，本文提出LMS-自适应滤波与EMD分解相结合的特征信号提取方法，并且通过模拟故障信号在Matlab中进行了仿真实验，得到了如下结论：LMS-自适应滤波算法可以有效地滤除电机振动噪声的干扰，使输入信号更接近未污染状态，并且可以有效抑制EMD分解过程中的模态混叠问题。

[参考文献]

[1] 胡爱军，孙敬敬，向玲.经验模态分解中的模态混叠问题[J].振动、测试与诊断，2011，31（4）：429-434.

[2] 张小明，唐建，韩锦.基于SVD的EMD模态混叠消除方法[J].噪声与振动控制，2016，36（6）：142-147.

[3] 黎恒，李智，莫玮，等.噪声干扰环境下抑制EMD模态混叠方法[J].信号处理，2015（8）：956-961.

[4] 肖瑛，殷福亮.解相关EMD：消除模态混叠的新方法[J].振动与冲击，2015（4）：25-29.

[5] 卢斌，何勇，刘传群，等.自适应滤波算法在纱疵信号去噪中的应用[J].自动化与仪表，2018，33（3）：46-51.

[6] 张艳艳，刘新平，邢素红.随钻测量信号去噪方法研究及实现[J].信息通信，2016（3）：49-50.

[7] 曹昌勇，方杰.基于Wiener自适应滤波算法在语音信号去噪中的研究[J].齐齐哈尔大学学报（自然科学版），2013（2）：12-16.

[8] 宋志环.车用驱动电机电磁振动噪声源诊断技术[J].电机与控制应用，2018，45（7）：97-101.

收稿日期：2020-04-16

作者简介：李杨（1994—），女，辽宁抚顺人，硕士研究生，研究方向：电力电子与电力传动。