解决问题
2020-08-31胡廷江李昕昕
胡廷江 李昕昕
题记:教学的最终目标就是“授之以渔”;解决问题的教学中让学生发现并提出问题、解决并剖析问题。将问题贯串教学过程,让问题成为知识的纽带,培养学生的问题意识和问题能力,是我们数学教学成功的关键,是现代教育追求的理想。
教学内容:人教版三年级下册第72页例8及相关练习。
教学目标:
1、进一步熟悉有关面积的知识。
2、经历运用长方形和正方形的面积计算公式解决问题的过程,进一步掌握解决问题的一般步骤,提高分析和解决问题的能力。
3、能运用所学的知识解决简单的实际问题,并对方案的合理性做出解释。
4、在解决问题的过程中让学生体验学习数学的价值,培养学生的应用意识和实践能力。
教学重难点:培养学生发现问题、分析问题、解决问题的能力。
教学准备:方格纸、多媒体课件
教学过程:
一、问题引入
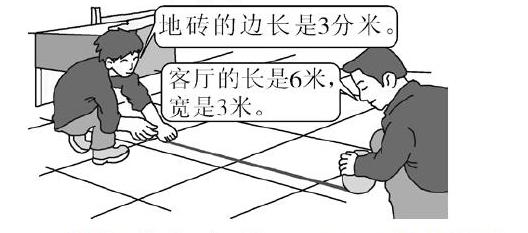
1、孩子们学习了长方形、正方形面积的知识,今天老师想请孩子们帮我家的客厅铺地砖,根据这个情景你能提出什么数学问题?
2、学生讨论,交流后重点引导学生讨论——“要买多少块地砖呢?”这个问题。(提前干预学生出错)
(1)要想知道应当买多少块地砖需要知道哪些条件?(地面的长和宽、地面的面积、方砖的长和宽、方砖的面积等)
(2)想一想给地面铺方砖时,能用方砖的边长或周长去铺地面吗?
(3)如果地面的大小不变,铺的方砖的大小不同,砖的块数会有什么不同?(地砖大,用的块数少,反之用的块数多。)
(4)地砖大是指的什么?(地砖的面积大)如果计算时,用面积大的地砖去铺比用面积小的地砖去铺用的块数还多,说明我们的计算肯定出错。需要孩子们重新计算找到出错的原因。
二、引领学生动手操作,找到解决问题的方案
(一)摆一摆,画一画,想一想
1、一个长5厘米,宽3厘米的长方形,想一想,用边长1厘米的小正方形把它铺满,需要多少个小正方形?(用学具摆一摆)
引导让学生说出自己的想法:
(1)摆一摆:一行要摆5个,要摆3行才能摆满。所以要15个小正方形。
(2)长方形的面积是15平方厘米,小正方形的面积是1平方厘米,15里面有15个1,所以要15个小正方形。
2、一个长6厘米,宽4厘米的长方形,想一想,用边长2厘米的小正方形把它铺满,需要多少个小正方形?(画一画)
放手让学生说出自己的想法,重点让学生找出两种方案的不同。
(1)看大长方形的面积里面包含了几个小正方面积,就需要多少块。(地面的面積÷地砖的面积=地砖的块数)
(2)先看铺一行要几块?(长6厘米能分成几个2厘米);再看要铺几行才能铺满?也就是一列要铺几块?(宽4厘米能分出几个2厘米)。用一行的块数×行数=地砖的块数。
3、想一想一个长方形的长9米,宽6米,用边长3分米的小正方形把它铺满,需要多少个小正方形?(能画吗?让学生画出示意图,然后说出自己的想法)
三、尝试解决例题
出示例8情景图。一共要用多少块地砖?
四、让学生独立完成后展示讲评学生不同的做法
1、方法一:
关键:用地砖的面积去铺客厅地面。
先求客厅的面积:6×3=18平方米=1800平方分米;
再求每块地砖的面积:3×3=9(平方分米);
最后求出地砖的块数:1800÷9=200(块)
剖析错因:
(1)6×3÷3错在哪里?(不是用边长去铺地面)
(2)6×3÷(3×3)又错在哪里?(没有统一面积单位)
(3)180÷9呢?(平方米和平方分米之间的进率是100)
2、方法二:
关键:摆一摆:
(1)一行要铺几块?
(2)要铺几行才能铺满?
先分别求出长和宽可以铺多少地砖:
长6米=60分米,每行铺地砖块数:60÷3=20(块)
宽3米=30分米,铺地砖块数:30÷3=10(块),也就是要铺满,要铺10行。
再求一共铺的地砖数:20×10=200(块)
剖析错因:
(1)6÷3=2(块)3÷3=1(行),2×1=2(块),错在哪里?
3、回顾与反思。
(1)通过以上的分析、解答,思考:如何对计算结果进行验算呢?
(2)学生讨论、交流。
(3)引导学生汇报、归纳。
验算:9×200=1800(平方分米)=18(平方米),结果与客厅面积相等,解答正确。在计算时,注意要将单位统一。
四、练习
1、完成教材第72页“做一做”。学生独立完成后,让两名学生在展台上展示不同的解法,然后集体讲评。
2、小青用边长5分米的方砖铺客厅地面,正好用了96块砖。客厅面积有多大?
五、全课小结
通过这节课的学习,你有什么收获?
板书设计:
