基于分数阶傅里叶变换和循环谱的雷达信号调制方式识别

张忠民，刘刚，刘鲁涛

哈尔滨工程大学 信息与通信工程学院，黑龙江 哈尔滨 150001

低 截 获 概 率(low probability of intercept，LPI)雷达具有低截获、高分辨率和抗干扰能力强等特点，传统的非合作截获接收机探测更加困难，所以明显提高了战场的生存能力，是军事领域反侦察、抗干扰的最有效技术之一。所以对LPI 雷达信号波形如何进行有效识别便成了非合作雷达信号处理研究的重点工作[1−3]。对于LPI 雷达信号波形识别的重点在于选取有效的信号特征和识别算法。早在20 世纪90 年代，A.K.Nandi 等[4−5]提出了一种基于时域瞬时和统计特征提取的雷达信号识别算法，当信噪比在10 dB 的情况下，对PSK、FSK 等信号的识别准确率达到了90%。但是对于多相码调制(如P1 码)，则无法进行有效识别。Barbarossa S 等[6−7]用Pseudo-Wigner 分布和Wigner-Ville 分布识别了线性调频信号和多种频率调制信号，对于相位调制类型的信号并没有进行研究。Lunden 等[8]提出基于CWD 和Wigner-Ville 分布(Wigner-Ville distribution, WVD)进行雷达信号识别的算法，识别了8 种雷达信号波形，信噪比在6 dB 的情况下，总体的识别准确率达到98%。但是在复杂的噪声环境下，由于算法对载波频率以及子脉冲宽度估计不准确导致了识别成功率的下降。文献[9]提出基于CWD 时频变换和图像处理等方法提取雷达信号波形特征，并结合ENN 神经网络分类识别，在信噪比−2 dB 条件下，对8 种雷达波形(LFM、BPSK、Costas、Frank 码、P1～P4码)识别率为94.7%，但是在工程实现上较为困难。戴亮军等[10]提出利用瞬时频率以及频谱的方法对信号进行分类，通过信号特征间的差异进行识别。文献[11]提出了基于频谱复杂度的识别方法，该方法使用信号的频谱复杂度的差异进行分类识别，但是在将信号进行平方后计算频谱复杂度进行信号区分的过程中，受噪声影响很大。

综上所述，为解决传统方法LPI 雷达波形特征提取困难、时频图像预处理过程复杂、低信噪比下多种类波形识别率低以及工程实现较为困难的问题，本文提出一种基于分数阶傅里叶变换和循环谱的方法。该方法利用分数阶傅里叶变换特征、频谱复杂度特征以及循环谱等特征实现几种常用雷达信号的分类识别。通过与文献[10]和[11]对比，结果显示识别率有很大提高，在低信噪比下仍然有很好的识别效果。

1 信号特征分析

雷达信号不同的调制方式可以体现在不同域中，如时域、频域以及时频域，由于信号的时域波形很容易受噪声的影响，根据信号的时域特征很难区分，所以，接下来利用信号在分数阶域上的特征，以及循环谱和频谱复杂度特征实现对雷达信号不同调制方式的分类。接下来针对NS、BPSK、QPSK、2FSK、LFM 和NLFM 这6 种常用的雷达信号进行研究。

1.1 分数阶傅里叶变换的基本理论

分数阶傅里叶变换表达式为

式中：P 是FRFT 的变换阶数； α是旋转角度；α=pπ/2。 参数P 以4 为周期，所以调整间隔在P ∈(−2,2]。 当 P=0时 ， X0(u)=X(u)； 当 P=±2 时，X±2(u)=X(−u)。

FRFT 用于信号识别，我们必须使用DFRFT数值运算。通过采样类型的Ozaktas 算法[12]映射时间的n 个采样点域原始功能，实现FRFT 快速算法，重写FRFT 表达式如下：

1.1.1 用于信号识别的FRFT 特征

FRFT 可用于信号识别的最重要原因是它对于LFM 具有出色的检测性能，因为FRFT 是线性的，而且可以进行旋转任何角度操作，LFM 在分数阶傅里叶域具有独特的能量聚集[13]，LFM 和编码信号可以通过在分数阶傅里叶域做二维峰值搜索进行区分。

下面对几种典型的调制信号及其FRFT 结果进行分析，仿真如图1 所示。

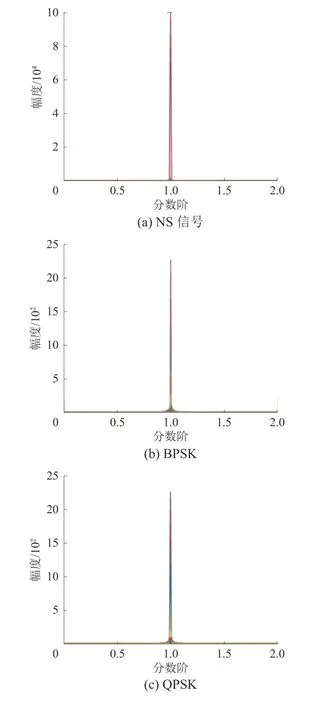
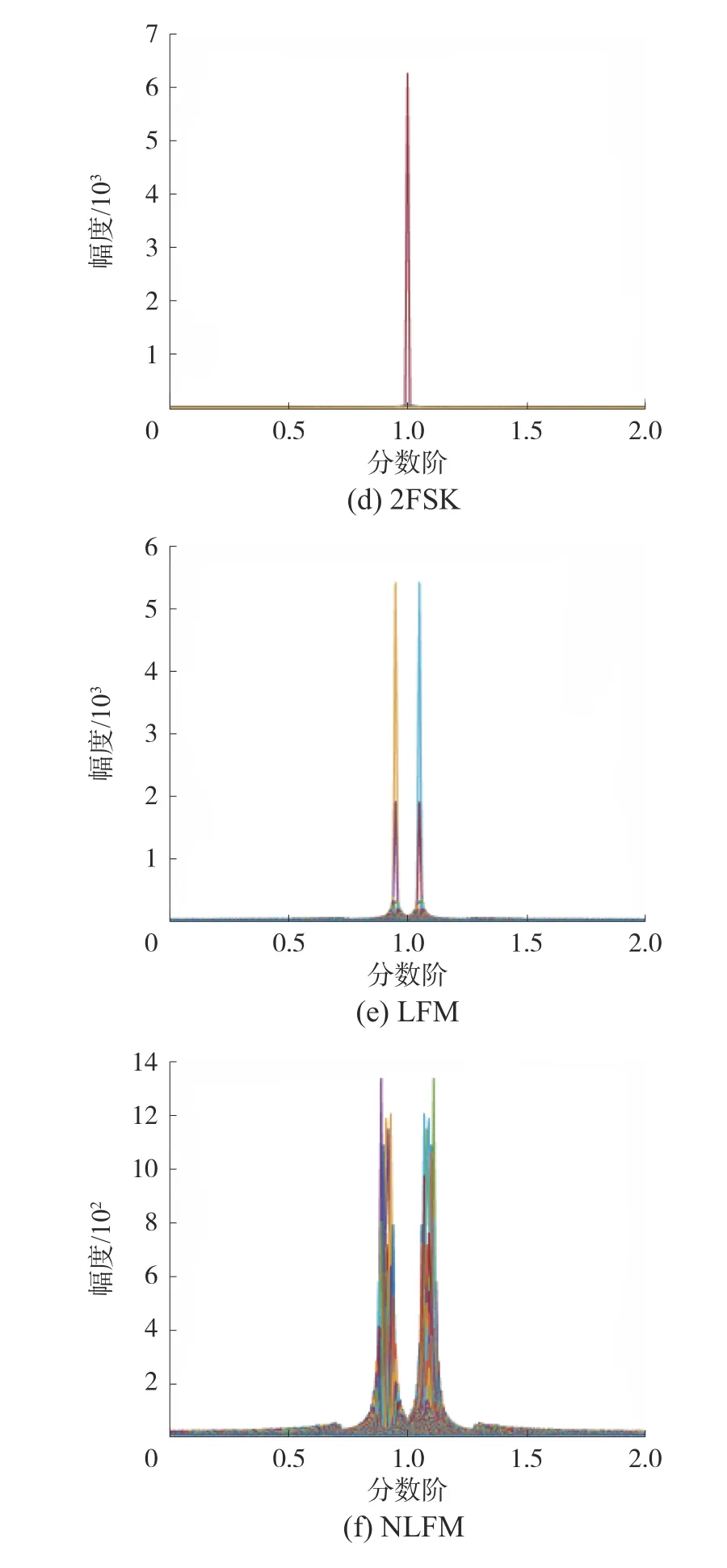
图1 6 种雷达信号的分数阶域曲线

仿真结果表明，编码信号的模量一定在P=1的位置，而LFM 信号的模量在P=1.25 的位置，不等于1。由于调频斜率的不同，对于不同的调频斜率，LFM 的峰值会出现在不同的值上，从而可以识别出LFM 信号和编码信号[14]。

在上述分析的基础上，总结了识别LFM 信号和编码信号的方法：将信号转换成分数阶傅里叶域，然后提取每个信号的最大模量对应的旋转角度；由此得到傅里叶变换的阶数，并根据阶数的不同位置对不同的信号进行区分；编码信号的模量在P=1 时出现峰值，而调频信号的模量在调频斜率匹配时出现峰值，即P≠1[15]。

从图1 可以看出，NS、BPSK、QPSK 和2FSK信号通过分数阶傅里叶变换后，在分数阶P=1 时模值会出现尖峰；而LFM 信号和NLFM 信号经分数阶傅里叶变换后，在P=1 处不会出现模值尖峰。所以以尖峰对应P 值是否为1 作为标准，可以将6 种信号识别为两大类[16]，即LFM、NLFM 调频信号为一类，NS、BPSK、QPSK、2FSK 非调频信号为另一类。

1.2 谱峰特征

对于2FSK 信号，利用其在频域上有2 个明显谱峰的特点将该信号与其他信号进行分类。为了减小噪声的影响，通过对信号频谱{s(k)}进行平滑操作处理，得到平滑后频谱{S(k)}，设定平滑步长是sstep，得：

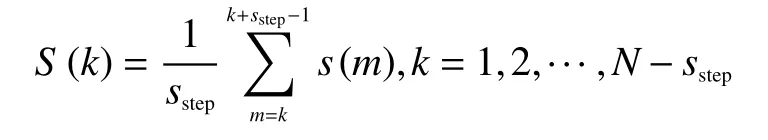
对平滑处理后的频谱{S(k)}进行谱峰搜寻，其过程如图2 所示，最终得到2FSK 信号处理前后的功率谱密度如图3 所示。

图2 2FSK 识别流程

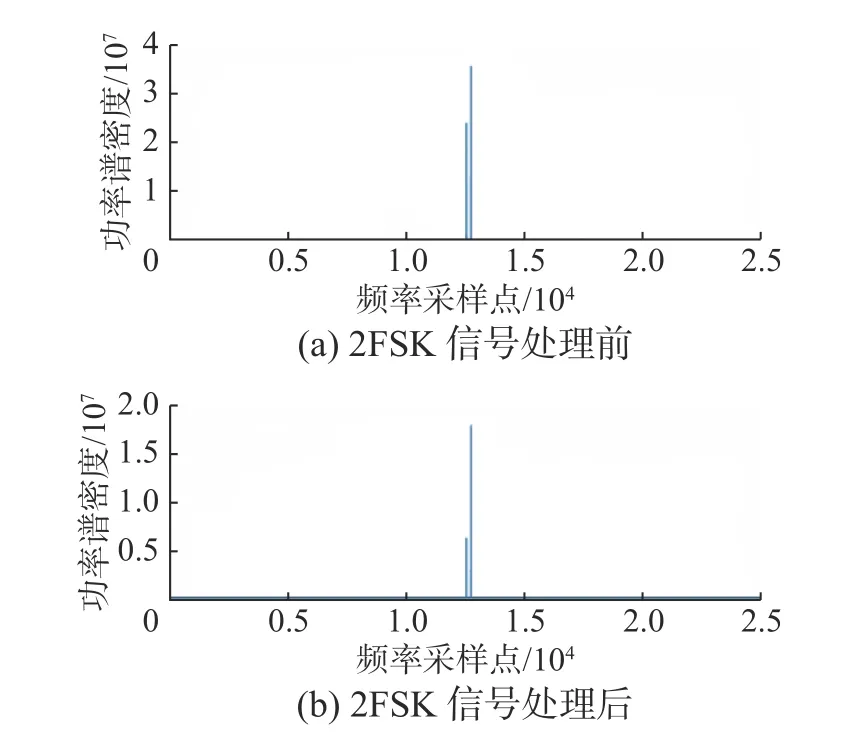
图3 平滑功率谱密度

从图3 可以看出，2FSK 信号的谱峰数为2，利用谱峰特征可以实现2FSK 信号与NS、BPSK、QPSK 信号的区分。

1.3 Lempel-Ziv(L-Z)复杂度特征

L-Z 复杂度用2 个简单的操作(复制和插入)表示序列特征，插入时间是复杂度，计算流程如图4 所示。

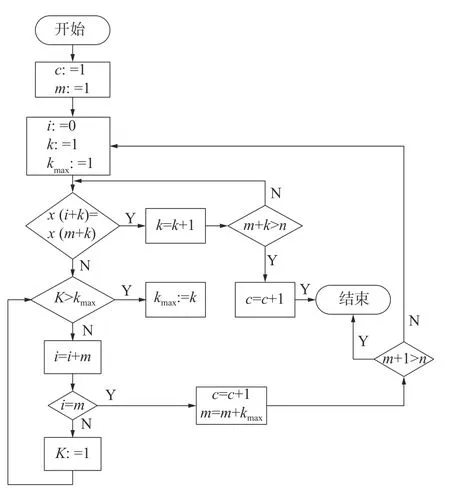
图4 L-Z 复杂度计算过程的流程

图4 中，c 为添加时间，即复杂度；m 是符号的个数，i 和k 是自然变量。

假设给定的字符串x(1)，x(2)，…，x(M)已由程序重建至数字x(M)，并且新插入了x(m) (即不通过简单地复制从x(1)，x(2)，…，x(M))。至x(m)的字符串将会用Y=x(1)，x(2),…，x(m)表示，x(m)是新插入的。为了检验剩下的Y，即x(m+1)，x(m+2)，…，x(M)是否可以通过简单的复制(或者是否需要插入新的数字)来重建，Lempel 和Ziv[17]进行了以下步骤：

1)集合Z=x(m+1)，确定是否可以从YZπ 中复制(YZπ 表示连接Y 和Z 新的字符串，然后删除最后一个符号)。

2)如果答案是肯定的，y 不变，但需要将下面的数字x(m+2)插入Z 中，则Z=x(m+1)，x(m+2)；如果答案是否定的，Z=x(m+2)，Y=x(1)，x(2)，…，x(m)，x(m+1)，继续判断。

3)重复步骤2)，直到Y 包含所有重建的数字，插入时间为L-Z 复杂度，表示为c(M)。但是，如果最后一个操作是复制的，则需要添加一个插入次数。

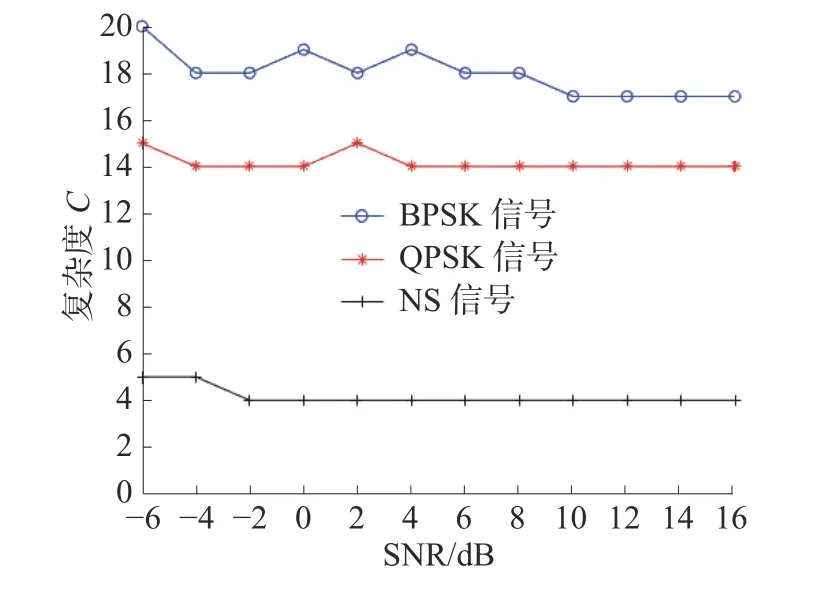
图5 BPSK、QPSK、NS 信号的频谱复杂度

从图5 可以看出，利用频谱复杂度可以实现NS 信号与BPSK 和QPSK 信号的区分。

1.4 循环谱

针对在低信噪比下对信号平方后频谱复杂度不够稳定、难以实现BPSK 信号与QPSK 信号的分类的问题，提出了循环谱的方法实现对BPSK和QPSK 信号的细分类。

对于循环平稳信号而言，其循环谱密度函数为循环自相关函数的的傅里叶变换[18]，表达式如下：

图6 BPSK 信号循环谱三维图

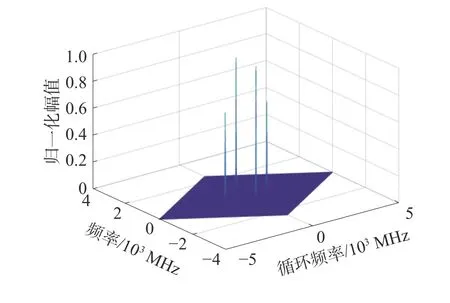
图7 QPSK 信号循环谱三维图

通过图6、7 信号循环谱三维图可以得到以下结论：

1)BPSK 信号的循环谱密度函数峰值出现在f=0 循环频率轴截面和α=±2f0上，而QPSK 信号的峰值不会出现在在α=±2f0处。

2)BPSK 信号循环谱密度函数的f=0 循环频率轴截面的最大值和在α=0 频率轴截面的最大值的比值非常接近1；而QPSK 信号两者之间的比值与1 相差很大。

所以根据结论2，定义循环谱在f=0 循环频率轴截面的最大值和α=0 频率轴截面的最大值的比值为λ，当比值λ 小于阈值时，判断为QPSK 信号，反之为BPSK 信号，如图8 所示。

(3)控制变量中，四种方法回归得出的成本收入比CRR的估计系数为负，且具有显著性，这表明盈利能力与成本收入比成反比．经营效率高的银行可以更好的统筹协调各部门业务往来，降低不必要的费用开支，提高收益．宏观经济水平GGDP的回归系数为正，均为显著，说明经济的增长对银行的盈利能力具有显著的正效应．而资本充足率CAR、存贷比LDR和对商业银行的盈利影响均不显著．

图8 BPSK 和QPSK 信号的λ 值

从图8 可以看出，利用循环谱的方法，在低信噪比仍然可以实现BPSK 信号和QPSK 信号的准确识别。

1.5 调频信号信号功率谱

非线性调频信号可以表示为

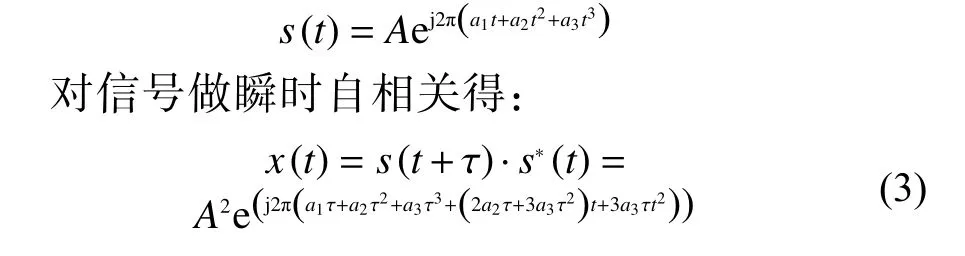
式中τ 为固定值。

式(3)变换为一个LFM 信号，如图9 中所示，其功率谱密度的外形特征近似为一个矩形。当信号s(t)为LFM 信号，此时a3=0，式(3)将转化为一个单载频信号，其功率谱密度在频域的外形特征表现为一根冲击谱线，所以，通过观察调频信号(LFM、NLFM)在瞬时自相关后的功率谱如图9，可以实现LFM 和NLFM 的细分类。

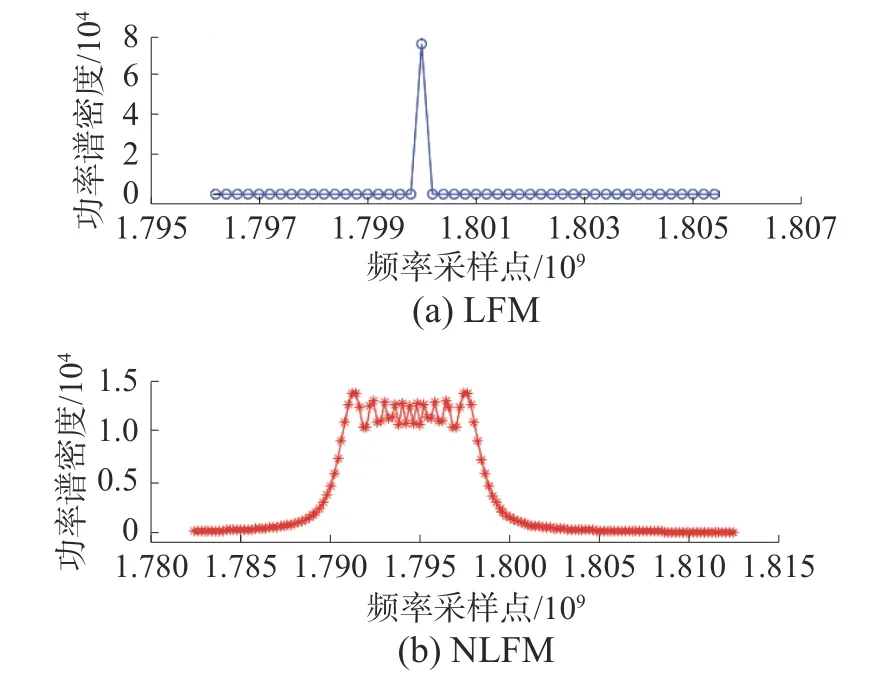
图9 瞬时自相关功率谱

2 信号识别流程

通过对调频信号以及非调频信号的特征分析，结合信号的分数阶傅里叶变换最大峰值对应的分数阶、信号复杂度和循环谱特征以及功率谱特征，设计如图10 所示的识别流程。

1)对接收信号进行分数阶傅里叶变换(FRFT)，分数阶记为P，P∈[0,2]，搜索出最大峰值对应的分数阶，记为P0。

2)根据P0是否等于1，将信号分为调频信号和非调频信号两大类[19]，调频信号包含LFM、NLFM 信号，非调频信号包含NS、BPSK、QPSK 和2FSK 信号。

3)对于非调频信号类进行处理。

①进行傅里叶变换，并对功率谱进行平滑去噪操作。搜索功率谱的谱峰个数n1，利用n1的值对信号进行判断，根据前文特征分析可知，2FSK 信号的谱峰个数n1为2，所以判断为2FSK信号，不然即为其他信号，再通过步骤②进行处理。

②对处理后的信号功率谱进行L-Z 复杂度计算，根据复杂度C 的大小，设定阈值为4。当C=4，判断为常规信号；否则判断为其他信号，再通过步骤③进行处理。

③计算循环谱在f=0 循环频率轴截面的最大峰值和在α=0 频率轴截面的最大峰值的比值为λ，当比值λ 小于阈值时，判断为QPSK 信号；否则为BPSK 信号。

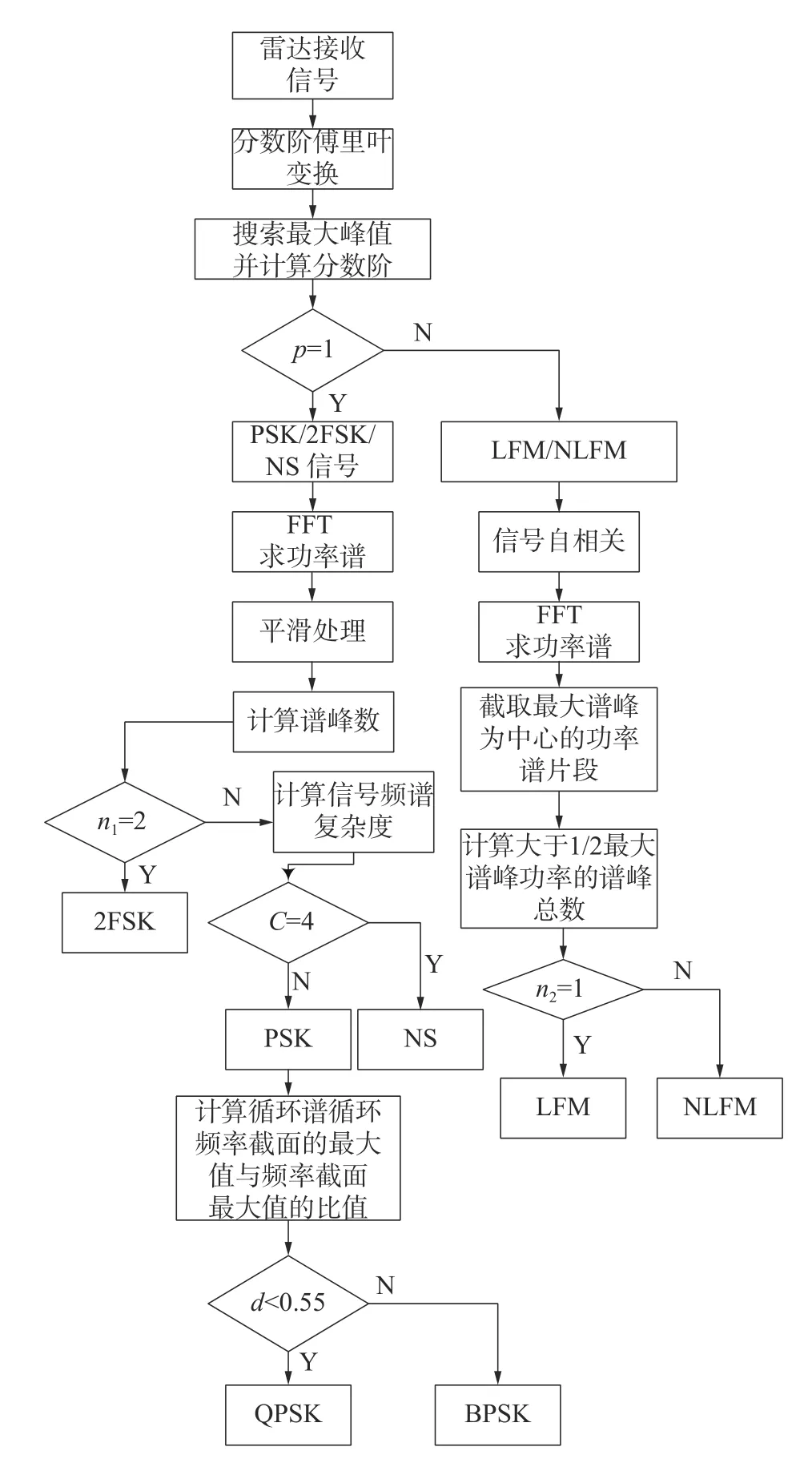
图10 雷达信号识别流程

4)对调频信号类进行处理。进行自相关傅里叶变换，求得其功率谱。由特征分析可知，线性调频信号会变换为单载频信号，其功率谱密度在频域的外形特征表现为一根冲击谱线，对功率谱进行谱峰搜索，当谱峰数n2等于1，即为线性调频信号；否则为非线性调频信号。

3 仿真结果与分析

实验参数的设定：信号的调制类型包括2FSK、BPSK、NS、LFM、QPSK 和NLFM 这6 种信号；脉冲宽度为5～30 μs；采样频率为500 MHz；载波频率为10～100 MHz；相位编码信号码元数为7～100；码元宽度为300～1 000 ns；频率编码信号的频率差为40 MHz；线性调频信号的带宽为5～100 MHz。通过1 000 次蒙特卡洛实验，绘制了在不同信噪比条件下的信号识别准确率图，如图11 所示。

图11 不同信噪比下的信号识别准确率

由图11 可以看出，BPSK 和QPSK 信号的识别效果最佳，信噪比在0 dB 时就达到了100%识别率，这是因为它的循环谱特征在噪声情况下表现稳定；NS 在低信噪比下识别率较低，因为频谱复杂度特征在低信噪比下不够稳定，但当信噪比为0 dB 时，识别率也达到了100%；当信噪比大于4 dB 时，LFM 信号和NLFM 信号以及2FSK信号的识别准确率都能够达到90%以上。因此可以说明利用谱峰搜索的方法进行识别是可行的，有着比较好的识别效果，将实验仿真结果通过与文献[10]比较，在低信噪比下，NS、BPSK、QPSK 信号识别率均大幅提升，其他不同调制类型信号在不同信噪比下也有所提高。

4 结论

1)根据信号的分数阶傅里叶变换最大峰值所对应分数阶以及雷达信号频谱等特点，设计了一个基于分数阶傅里叶变换及循环谱的雷达信号识别方法。实验结果显示，在信噪比为2 dB 的情况下，信号的总体识别准确率可以到达90%，所以该方法有很好的识别效果。

2)针对BPSK 及QPSK 信号，平方后利用频谱复杂度的方法受噪声影响太大，提出了利用循环谱的特征进行区分，在低信噪比下依然可以区分。

3)本文所用到的信号都是变化的，更接近于实际信号，具有较好的工程应用价值，虽然针对这6 种常用信号有着很好的识别效果，但过程较为复杂，如果要识别更多的信号，接下来需要研究更具有普适性的算法。