融合相邻单元高低页存储可靠性的闪存译码算法

郑敏华，韩国军

广东工业大学 信息工程学院，广东 广州 510006

近几年，NAND 闪存因为其高存储容量、快速读写、非易失性、低成本以及体积小等优点，被广泛应用于各类电子产品和数据存储中心。随着闪存工艺水平的发展，闪存芯片的尺寸由早期的50 nm缩减到20 nm 以下，使得闪存密度显著增大，相邻闪存单元距离越来越近，单元间干扰加剧[1−4]。同时，闪存在使用过程中存在不同程度的磨损，氧化层的绝缘性降低导致电子泄露从而引起持久性噪声，使得存储单元的阈值电压随时间向较低状态偏移[5−8]，闪存的数据可靠性和使用寿命都不同程度降低。为了提高MLC 闪存的传输完整性，可对信号进行数据后补偿或数字预失真的信号处理方式。其中，Adnan[8]利用闪存持久性噪声的特点对第一次译码错误的比特置信度进行修正，并重新译码。另一种算法[9]通过大量的译码数据样本找出更为准确的阈值量化电压。然而，这2 种算法复杂度高，鉴于此，本文利用闪存读取顺序和编程顺序之间的关系，通过相邻字线低页的译码信息来辅助改善高页的纠错性能，并利用译码过程中校验信息与置信度的关系来辅助改善低页的纠错性能。

1 信道模型

MLC 闪存信道的建模如图1 所示，数据先通过擦除与编程操作写入存储单元。不失一般性，闪存信道的干扰主要包括随机电报噪声[10−11]、持久性噪声和单元间干扰。

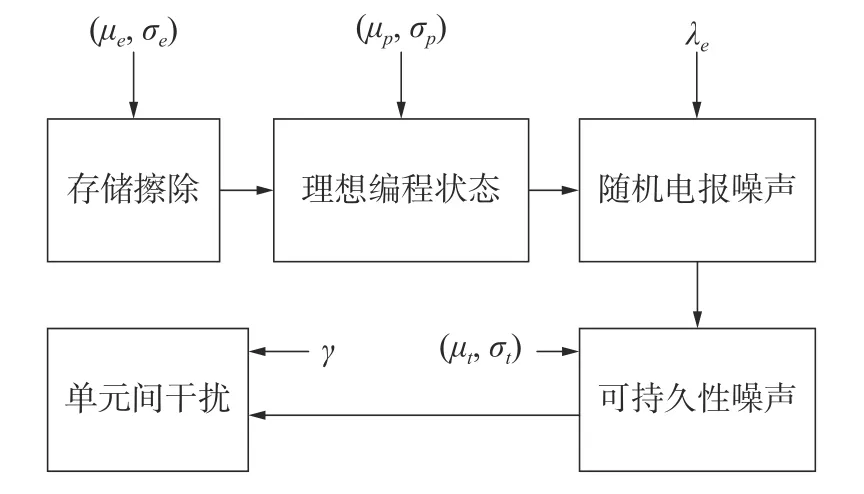
图1 MLC 闪存信道模型

1.1 擦除与编程操作

由于闪存的物理结构，不能直接改变闪存单元内的电子数量来完成编程，因此需要对整个闪存块进行擦除操作，再进行编程操作。处于擦除状态与编程状态下的阈值电压均服从高斯分布。

擦除状态下阈值电压概率密度函数为

式中： µe和 σe分别表示擦除状态下阈值电压概率密度函数的均值与标准方差， µp和 σp分别表示编程状态下阈值电压概率密度函数的均值与标准方差。

当前闪存采用的编程顺序为坡度编程顺序[5,12−13]，如图2 所示。对每个字线(记为WL i)的高页(记为MSB)与低页(记为LSB)都进行编号，并按编号从小到大的顺序进行编程。除了WL 0 对应的LSB 的编号为0 和最后的字线WL n 对应的MSB 的编号为2n+1，WL i 对应的LSB 的编号为2i−1，对应的MSB 的编号为2i+2。

图2 编程顺序

1.2 随机电报噪声

随着编程和擦除次数的增加，干扰也会增加，导致阈值电压向两侧漂移，随机电报噪声服从指数分布，其概率密度函数为

1.3 持久性噪声

闪存氧化层的绝缘性能会随着PE的增加而降低，使得电子泄露得更快，导致阈值电压向左偏移。持久性噪声服从高斯分布，其概率密度函数如下：

式中： µt=KS(Vs−x0)·[At(PE)ai+Bt(PE)a0]·log(1+T)，其中， Ks、 x0、 At、 Bt、 αi、 α0都是常数， T为持久性噪声时间； σt=0.3·|µt|。

1.4 单元间干扰

当闪存结构为干扰较小的全位线结构时，由于相邻闪存单元间寄生电容耦合效应，如图3 所示。因此，单元间干扰可用每个闪存单元的阈值电压变化量的线性组合来表示：

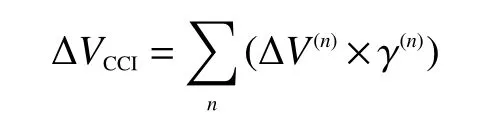
式中 ∆V(n)和 γ(n)分别表示第n 个干扰单元的阈值电压变化量和寄生电容的耦合系数。其中 γ有2 种形式： γy为垂直相邻方向和 γxy为斜对角相邻方向，令 γy=0.08s 和 γxy=0.006s ， s为单元间干扰影响因子。

图3 全位线结构下的单元间干扰示意

阈值电压的条件概率分布函数在受到随机电报噪声、持久性噪声和单元间干扰后的数学表达式为

图4 是MLC 闪存信道在单元间干扰下的阈值电压分布图。状态‘11’为擦除状态，不对相邻单元产生单元间干扰；状态‘10’、‘00’和‘01’为编程状态，会对相邻单元造成单元间干扰，因此大部分闪存单元会受到单元间干扰，阈值电压向右移。

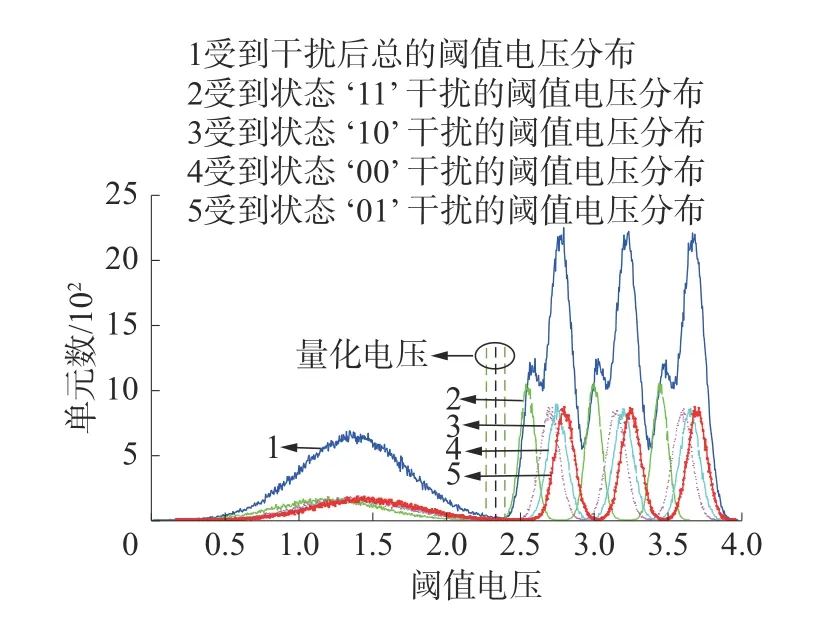
图4 MLC 闪存信道在单元间干扰下的阈值电压分布(s=1.6 、 PE=10 000、T =0)

2 优化方案

如图4 所示，状态‘11’与‘10’的重叠区设有3 个量化电压，同样地，状态‘10’与‘00’的重叠区和状态‘00’与‘01’的重叠区也设有3 个量化电压,共9 个 量 化 电 压 R={Ri|i=1,2,···,9}，其 中R2、R5、R8为硬判决电压。这9 个量化电压把MLC 闪存阈值电压划分为10 个阈值电压区域，并按阈值电压从小到大的顺序对阈值电压区域进行标号{flag(m)=m|m=1,2,···,10}。

存储单元上不同页的错误概率是不平衡的，通常高页(记为MSB)的错误概率比低页(记为LSB)的错误概率高，同一个存储单元上的2 个比特的可靠性不同[2]，并用置信度信息表示比特的可靠性，作为译码时的初始化信息。为了减少计算复杂度，定义MSB 与LSB 的置信度(可靠度)信息为RMSB(i) 和 RLSB(i),i=1,2,···,N，N 为码长，如图5 所示。

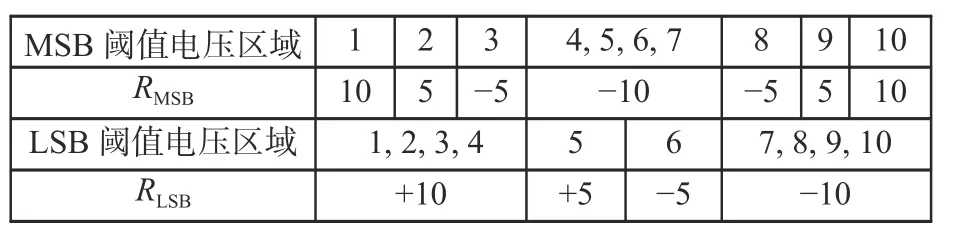
图5 MSB 和LSB 的置信度信息赋值

2.1 利用相邻低页修正高页

闪存在相同干扰下通过阈值量化电压对整体阈值电压进行量化，并不能确保该量化电压满足闪存每一字线的阈值电压量化，存在量化电压补偿不足和过渡补偿的可能。如图6 所示。当阈值电压右移严重时，量化电压会出现补偿不足的情况，使得圆形标注的闪存单元在阈值电压量化后为‘10’状态的单元，因此其置信度信息赋值为RMSB(3)。而当阈值电压右移不严重时，量化电压会出现过渡补偿的情况，使得三角形标注的闪存单元在阈值电压量化后为‘11’状态的单元，因此其置信度信息赋值为 RMSB(2)。A2 状态重叠区也出现同样的置信度赋值错误，因此需要对译码错误的MSB 状态重叠区的置信度进行纠正。

图6 MLC 闪存信道高页重叠区置信度错误分析

根据闪存的读取机制[4,13−14]，可同时读取到WL i 的MSB 和LSB，由 图2 可 知，在WL i 的MSB 编程前，WL i+1 的LSB 已完成编程。因此，当读取到WL i 的MSB 时，结合闪存的编程顺序可 读 取 到WL i 的LSB(记 为LLSB)和WL i+1 的LSB(记为NLSB)，则译码错误的MSB 可利用LLSB和NLSB 的译码信息。

首先找到译码失败的MSB 重叠区中的闪存单元在码字中的位置U。若译码错误的MSB 读取到的LLSB 和NLSB 都译码正确，说明LLSB和NLSB 的译码信息可靠。则译码失败的MSB 可利用译码成功的LLSB 和NLSB 在位置U 上的比特值来确定MSB 重叠区中置信度赋值错误的比特位，并纠正其置信度信息。比如，当RMSB(U)==−5,BLLSB(U)==1时，该闪存单元在[R2,R3]区间内，若BNLSB(U)==0，说明该字线阈值电压右移严重，使得量化电压补偿不足，则修正其置信度RMSB(U)==RMSB(2)。具体过程如算法1。

算法1 利用相邻低页信息辅助修正高页

1)若MSB 译码失败，LLSB 和NLSB 都没有译码成功，则执行步骤5)。

2)读取LLSB 和NLSB 在译码后的比特信息，并分别记为 BLLSB(i)和 BNLSB(i),i=1,2,···,N，其中N 为码长。找出MSB 的变量节点{vi∈flag(2,3,8,9)}的位置U， U=find(RMSB==|5|)。

3)读取并更新MSB 重叠区中错误比特的自信度信息：

4)该译码错误的MSB 页重新BP 译码。

5)结束。

算法1 的延伸：在译码错误的MSB 读取到的LLSB 和NLSB 中，会出现只有一个译码成功的情况，则此LLSB 和NLSB 并不完全可靠，在位置U 上的比特值未必正确。而阈值电压区域对应的置信度信息表示该阈值电压区域的可靠性，因此可判断LLSB 和NLSB 在位置U 上的置信度信息是否可靠，若可靠则表明LLSB 和NLSB 在位置U 上的比特信息可靠。由已发表的大量文献[15−18]可知，LSB 只有一个状态重叠区，相比LSB 其他区域的可靠度要低很多。如果LLSB 或NLSB在位置U 上的置信度信息是LSB 在状态重叠区的置信度信息，则LLSB 和NLSB 在位置U 上的比特信息不可靠，若(RLLSB(U)!=|5|)&&(RNLSB(U)!=|5|)，进行算法1 的步骤3)。

2.2 修正低页

由于在算法1 中，找出MSB 状态重叠区置信度信息赋值错误的比特需要借助LLSB 和NLSB的译码信息，若LLSB 和NLSB 译码失败会影响MSB 的修正，所以需要提高LSB 的纠错性能。

在状态‘10’和状态‘00’的重叠区中，存在着少量LSB 可靠性低的变量节点 vf∈flag(5,6)，该部分变量节点通过校验节点ci的更新[19−20]，如式(1)；传递可靠性低的信息给其他变量节点 vj∉flag(5,6)。变量节点vj通过更新节点信息，如式(2)；对外传递含有vf的信息。并在完成一次译码后计算vj的总信息，如式(3)；并进行硬判决，如式(4)。

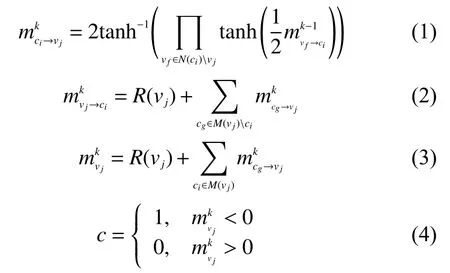
由式(1)～(4)可知，可靠性低的变量节点有可能会影响到可靠性高的变量节点总信息的计算及其向外传递信息的可靠性，从而影响硬判决，导致可靠性高的比特翻转。在闪存信道内，LSB 的变量节点 {vi∈flag(1,10)}的可靠性高，比特错误率低[15−17]，且比特数几乎占了一个码字的一半。为了防止LSB 的变量节点 {vi∈flag(1,10)}的比特因为错误的变量节点导致翻转，对比了255 帧LSB 在不同单元间干扰影响因子s 下，LSB 的变量节点{vi∈flag(1,10)}在传统BP 译码算法和无算法译码(硬判决)下的总比特错误量，如表1 所示。

表1 BP 译码算法和无译码下‘11’和‘01’的总比特错误量

对LSB 的变量节点 {vi∈flag(1,10)}不进行译码直接硬判决，由表1 可推断：

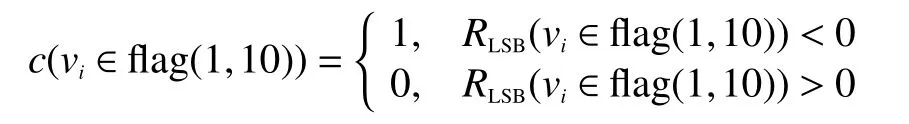
经过BP 译码后，LSB 的变量节点vi∈flag(1,10)中存在少量错误比特，则该错误比特的总信息与置信度信息的正负关系为

因此根据式(3)，可得出该错误比特的总信息与校验信息的正负关系为

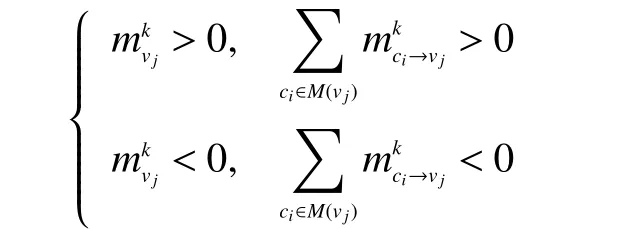
所以该错误比特的置信度与校验信息的正负关系是

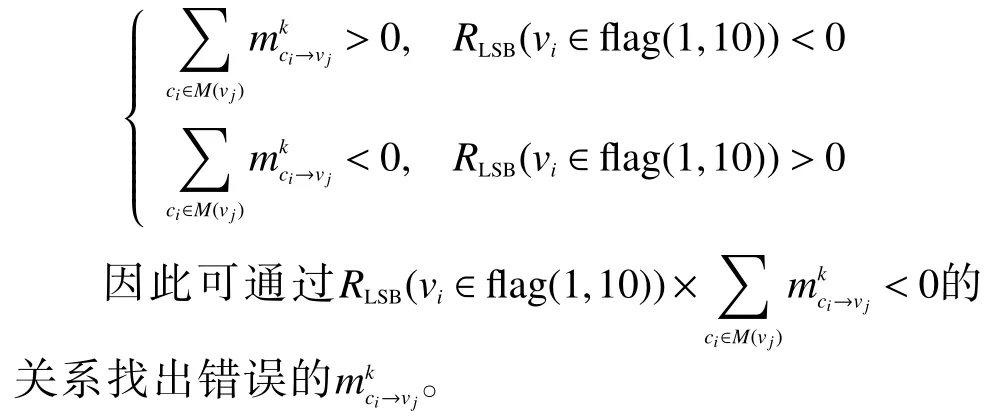
由以上推导可知，可靠性高的比特会因接收到可靠性低的校验信息而发生翻转，因此对校验信息增加可靠性权重a。为了去除可靠性低的校验信息对可靠性高的比特造成影响，令a=0；若校验信息可靠则保留，令a =1。具体过程如算法2 所示。

算法2 增加LSB 加权可靠度

2)更新校验节点，计算式(1)。

3)更新变量节点，计算码字总信息。

if {vj∈flag(1,10)|vj∈LSB}

更新式(2)变量节点，计算式(3)码字总信息。

else 计算式(3)，并计算校正信息可靠性权重：

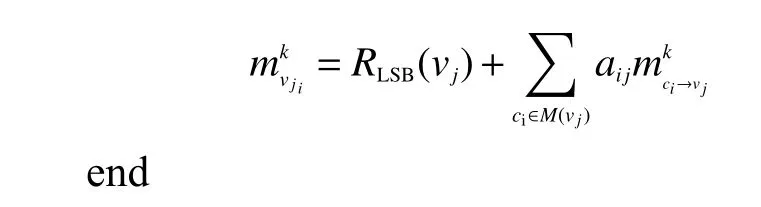
4)硬判决式(4)。

5)若满足 c·HT=0，则停止迭代，否则继续重复步骤2)、3)，直到满足 c·HT=0或迭代到最大迭代次数 Imax。

3 仿真结果

本实验仿真是在MATLAB 平台上实现，所有算法都基于传统并行BP 译码算法上进行改进，在每一算法中MSB 和LSB 同时参与译码，参数T =0,PE=104。图7 表示的是在不同的单元间干扰影响因子s 下，MSB 重叠区域的错误比特数以及MSB 的误码率和误帧率在传统BP 译码算法和算法1 及其延伸算法下的比较。当s=1.4 时，算法1 及其延伸算法的误码率降低尤为明显；当s 逐渐增大，算法1 的延伸比算法1 有更明显的性能提升。算法1 及其延伸算法通过结合闪存的写入与读取机制，通过相邻字线LSB 的译码信息，有效确定译码错误的MSB 重叠区中置信度赋值错误的比特，并对其进行改正，能大幅度提升译码性能。

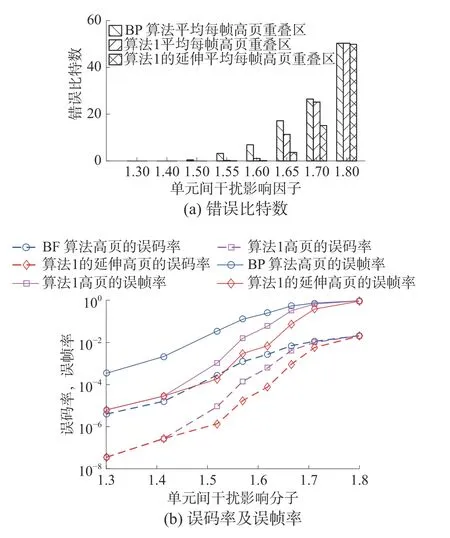
图7 BP 算法和算法1 及其延伸算法性能分析

图8 表示在不同的单元间干扰影响因子s 下，状态‘11’和状态‘01’在LSB 非重叠区下的错误比特数，以及LSB 的误码率和误帧率在传统BP 译码算法和算法2 下的比较。可见LSB 中变量节点vi∈flag(1,10)的校验信息，在传统BP 译码算法下，受到可靠度低的变量节点的影响很大，导致少部分该变量节点的比特发生翻转。算法2 通过这部分变量节点的置信度信息与校验信息之积的正负信息来计算校验信息的可靠性权重，能有效降低这部分的错误比特数，提高译码性能。

图8 BP 算法和算法2 性能分析

4 结论

根据高密度NAND 闪存数据的写入与读取机制，以及高低页比特之间的关联关系，提出了一种融合相邻单元高低页存储可靠性的BP 译码算法。

1)算法1 利用读取顺序与编程顺序之间的关系，通过相邻字线的译码信息来辅助改善高页的纠错性能。由于算法1 性能的改进需通过相邻字线，因此提出算法2 来改善相邻字线的纠错性能。

2)算法2 利用了可靠性较高的比特位上的总信息求和，对该比特位接收到的校验信息增加可靠性权重，保证可靠性较高的比特位向外传递信息的可靠性，并防止可靠性较高的比特位翻转。理论分析以及数据的仿真表明该算法能够有效提高纠错性能。