基于PEEK注塑的石油电连接器仿真与设计研究

王敏兴，朱 赫，杜建东

(贵州航天电器股份有限公司，贵州贵阳，550009；苏州华旃航天电器有限公司，江苏苏州，215129))

1 引言

由于各种石油、矿井勘探开采设备的大量使用，电连接器和接插件得到了蓬勃的发展，目前连接器的结构主要分为矩形连接器、圆形连接器等。由于石油设备需要承压设计,设备一般采用圆形结构设计，设备内部转换器和电连接器以圆形为主。根据使用环境和成本要求，石油连接器分为承压电连接器和非承压电连接器，其中承压电连接器又可分为玻璃烧结电连接器[1]和PEEK注塑电连接器[2]。近年来，研究者和工程师们提出了不同设计结构提升PEEK注塑电连接器的耐液压能力和耐温能力，文献[3]提出一种CAE技术在注塑成型中的应用。本文通过热与结构仿真，快速提升产品的研发速率，并实现耐压140MPa、耐温200℃，耐压175MPa、耐温175℃产品的研发。

2 热与结构力学耦合模型的建立

为了解决注塑连接器耐高温、耐高压力的问题，本文接下来提出了一种耐高温高压的多芯注塑连接器的结构设计，使得电气性能满足耐压1000VAC，漏电流小于5mA；绝缘性能5000MΩ@500VDC；气密性满足1×10-3Pa.cm3/s。

2.1 电连接器的结构设计

本文电连接器采用支撑环和插针直接注塑成型，其几何三维结构设计模型如图所示。

图1 连接器几何结构设计模型

根据设计目的，并结合图1可知，当连接器承压时，支撑环端面作为支撑面承压，支撑环与peek体的接触面积与相同温度下的压力成正比。

根据连接器的结构设计图可知，其热量传导模型可简化为：外部环境、peek介质、金属插针，且体积裁剪方式降低仿真计算量、提高计算速率，多芯注塑连接器的热传导有限元模型如图2所示，其在热传导分析可简化为单芯模型，如图3所示。

图2 多芯连接器的热传导有限元物理模型

图3 连接器简化模型的热传导有限元物理模型

2.2 连接器压力与热传导计算

由于石油连接器承压为轴向承压，其承压能力取决于结构设计和材料的弯曲强度，根据连接器的结构设计，温度恒定条件下，连接器的承压能力方程可表示为

(1)

式中：P——连接器承受的压强；

S——连接器的承压面积；

s——轴向非支撑的面积；

Pf——初始压强。

由公式1可知，温度恒定环境下，支撑面积越大，承压能力越强，故本文采用支撑环开孔式设计。

由于电连接处于温度浮动较小的环境中，可认其工作环境为热稳态环境，即认为通过传导传递给表面的能量与通过对流传递的能量相等。

从工程设计考虑，石油类连接器一般为圆柱形结构，对连接器进行物理模型简化成复合材料圆筒壁导热结构，并搭建其数学模型，其数学模型如图所示。

通过数学模型建立圆柱坐标系，壁内的温度仅沿着径向R进行传导，其中内径为r1、外径为r2、长度为l，内外壁表面分别为均匀稳定的温度tw1和tw2，且tw2>tw1。

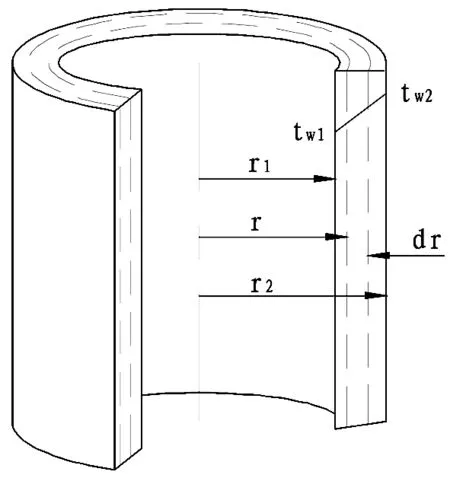
图4 热传导数学模型

根据傅里叶导热定律，并结合连接器的热传导有限元模型，求解出连接器不同界面的温度。

傅里叶导热定律为

(2)

式中：qx——传热率在x轴的分量；

h——介质的导热系数；

A——垂直于热流的面积；

负号——热量沿温度降低的方向传递。

根据傅里叶导热定律推导出连接器热量传导矩阵方程为

(3)

其中，h1、h2、A1、A2、T1、T4已知，故可求出T2、T3。

2.3 结构应变和热应变的计算

根据连接器的承压特征，连接器在外部压力的作用下，发生轴向压缩，其轴向应变计算方程为

(4)

式中：ε——结构应变；

σ——平均应力；

F——压应力；

E——材料的弹性模量；

A——承压面积。

根据材料温度特性，连接器随着温度升高，发生轴向和径向的热膨胀，其热应变公式为

ε=α(T-Tref)

(5)

式中：ε——热应变；

α——热膨胀系数；

T——实际环境温度；

Tref——基准环境温度。

通过peek材料牌号的选定，其材料的物理参数均为固定，可计算peek材料压力和温度条件下的应变，以及温度条件下的应变。

3 PEEK注塑模流仿真分析

本文采用软件对PEEK注塑的过程进行模流分析，主要分析注塑过程中peek收缩率大小和各向收缩率的差异，以及peek流动性、结晶性等。

3.1 模流仿真分析

根据PEEK注塑产品设计模型进行模流分析，其产品模型如图5所示。

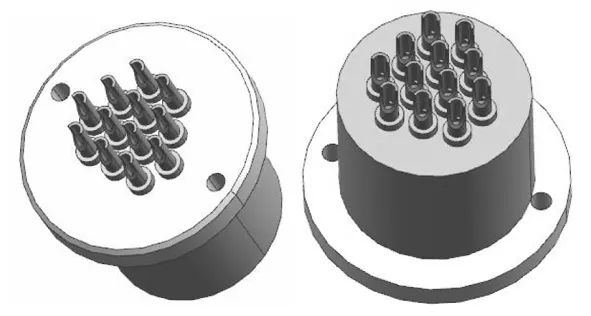
图5 多芯连接器注塑合件模型

注塑温度的控制尤为重量，它不仅能够保证料的流动性，而且能够使得peek颗粒结晶一致性较好，避免结晶度不均匀的问题，图6为peek料流动前和填充后的温度模型。

由于注塑过程是peek料体承压的过程，随着温度的变化，peek材料在成型过程中存在一定的气孔，且材料存在有一定的收缩性，两者均关乎注塑合件的承压特性和成型尺寸，图7为注塑合件的缩痕指数和气穴分布。

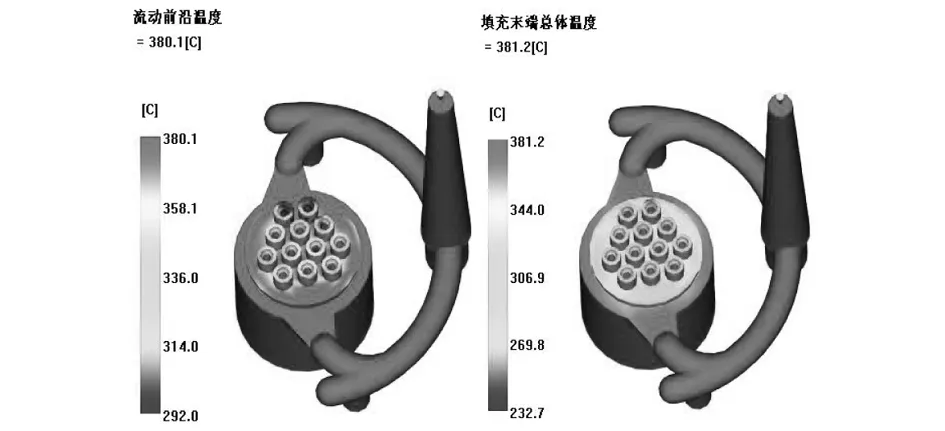
图6 peek料流动前和填充后的注塑模的温度分布图

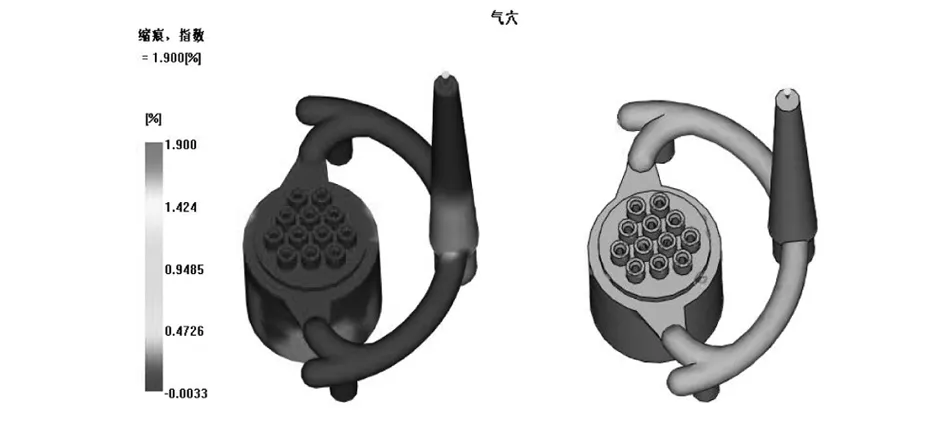
图7 注塑合件的缩痕指数和气穴分布图

注塑合件其变形直接影响产品的密封性和安装尺寸，通过注塑模流对注塑合件进行模流分析，如图8所示。

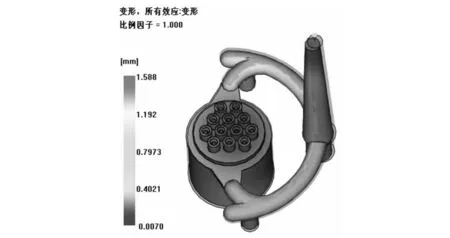
图8 注塑合件的变形图

由模流分析图8可知，注塑合件的形变为主要集中在0.01mm左右。

3.2 注塑产品分析

注塑件的重量是衡量注塑结构可靠性的一个重要指标，本文通过对26件注塑产品进行重量统计分析，如表所示。

表1 26件产品的重量统计分析

由表可知，考虑支撑环和插针因公差导致产品重量不一致，在此取0.02g作为划分差，产品重量服从高斯分布，主要集中在22.48g-22.54g范围内，产品重量一致性较好。

4 热与结构力学耦合仿真

本文首先在仿真软件中采用(热)求解器进行分析，再使用热和结构力学进行耦合分析。

4.1 电连接器的热仿真

本文采用仿真模拟连接器的真实工作环境，求解连接器在200℃条件下的注塑材料的膨胀特征[4]，以检验注塑连接器在热环境下，是否会引起气密性不良。

图9 单针的径向热膨胀

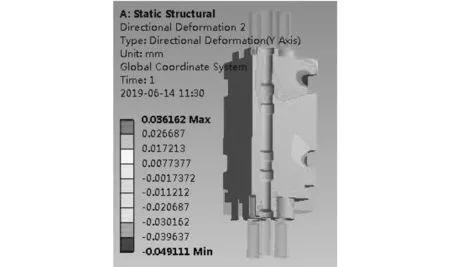
图10 peek基座的径向热膨胀图

由于多芯注塑连接器的基座呈圆柱状结构，为了降低计算量、加快仿真速度，本文对模型进行简化，简化为1/4结构，图9为分析单针径向热膨胀图，图10为peek基座的径向热膨胀图。

由图9可知，插针的径向膨胀0.018mm，插针为对称结构，其在密封环境内受热均匀，其膨胀呈对称趋势。

基座的径向膨胀0.007至-0.01mm范围内，其值小于插针的径向膨胀尺寸，可判断为插针与基座紧密接触，不会发生泄漏。

4.2 电连接器的热与结构力学仿真

注塑电连接器在相同材料和高温条件下的承压能力，取决于PEEK材料的热条件下的抗拉强度，以及产品支撑环的支撑面积[5]，本文支撑环设计为圆盘开孔式，此种方式增加了金属支撑环对peek基座的支撑面积。

本文对注塑连接器加载温度条件为200℃和压力条件为140MPa，网格划分采用6面体方式，其仿真结果如图11基座的应力分布图；图12注塑连接器的形变分布图；图13为基座的形变分布图。

图11 连接器基座的应力分布图

由图11可知，基座的应力主要分布在支撑环接触部和基座顶部，其最大值分布在支撑环过孔处，其值为74MPa左右，其值小于PEEK在200℃条件下的弯曲强度，如表2所示。

图12 连接器的形变分布图

由于连接器顶部为承压端，参考面为支撑环，尾端为正方向，通过图12可知，连接器的形变最大集中在顶部，其值最大为0.215mm。

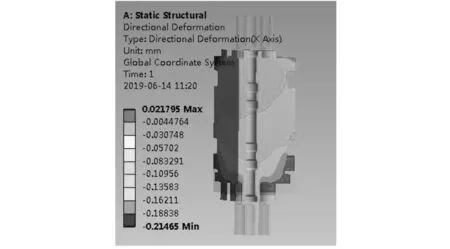
图13 基座形变分布图

由图13可知，参考面为支撑环，方向朝顶端为正方向，最大形变位于基座与支撑环的接触面，其最大值为0.215mm。

4.3 温度对材料机械性能的影响

PPEK材料作为一种耐高温、自润滑、易加工的工程塑料，其在石油连接器领域有着广泛的应用，但其弯曲强度随着温度的升高而降低，表1为peek材料温度与机械性能(弯曲强度)之间的关系。

表2 材料与温度的线性关系

本文对比两种常用的加30%玻纤的增强型peek料，其弯曲强度随着温度的升高，不断降低，两者相比较，结合仿真分析多芯注塑连接器的最大应力在74MPa左右，22GL30的材料能够满足本文所述多芯注塑连接器在200℃和160MPa的使用环境。

5 结束语

本文提出了利用仿真分析的方式，验证注塑电连接器设计的合理性和可行性。首先，建立热与结构力学耦合模型；其次，对PEEK注塑模流进行仿真分析，最后对热仿真、热与结构力学耦合仿真进行分析研究。使得本文设计的注塑电连接器满足使用环境为140MPa、200℃和175℃、175MPa两种环境的条件。