基于强化学习的苏拉卡尔塔博弈算法

王仁泉， 丁 濛， 李淑琴， 石露颖， 戚译中， 刘朔言

（北京信息科技大学 计算机学院， 北京100101）

0 引 言

自计算机诞生以来，机器博弈就是其重要的研究方向，被称为计算机领域的“果蝇”。 很多人工智能领域的方法及技术都在其上进行了实验和应用。

机器博弈研究的发展主要分为两个阶段。 第一阶段，利用手工构造的估值函数权重，辅以搜索树剪枝，以降低计算复杂度，这个方法也被称为传统方法。 在此期间，最引人注目是1997 年，深蓝打败了国际象棋大师加里· 卡斯帕罗夫（ Garry Kasparov）［1］。 但传统方法面临着两大挑战：一是手工构造的估值函数实际上是一个专家系统，对函数的构造具有很高的要求；二是计算难度大，Allis 曾计算［2］出，国际象棋搜索树的复杂度为10123、中国象棋为10150，而围棋的搜索树复杂度则为10360，这对机器的运算能力提出巨大的挑战。 鉴于以上原因，近年来许多学者引入人工智能的自学习方法进行优化和学习，使机器博弈进入第二阶段，即机器学习方法。 主要方法包括差分学习方法［3-5］和基于蒙特卡洛树搜索的神经网络方法［6］。 将人工神经元引入机器博弈的评估函数，通过强化学习方法，表现了走子的内在逻辑和潜在规则。

本文介绍了自学习方法与苏拉卡尔塔棋机器博弈的阶段性成果，该方法主要是将神经元与蒙特卡罗方法结合，引入苏拉卡尔塔机器博弈的评估函数，通过自对弈方法，获得大量对局数据，并通过反向传播算法［7］提高神经网络的评估能力。

程序的代码已经发布： https：／／github.com／jimages／surakarta－cpp

1 苏拉卡尔塔棋简介

苏拉卡尔塔棋（Surakarta）是源自印尼爪哇岛的两人吃子类别的游戏。 棋盘由6x6 的正方形网络和4 个角落上的圆弧构成，正方形网格构成的交叉点为落子的棋子位置。 双方采用不同的颜色，各十二枚，一般采用黑白或者红黑两色。 棋局开始时，双方在各自的底线排成两排，如图1 所示。

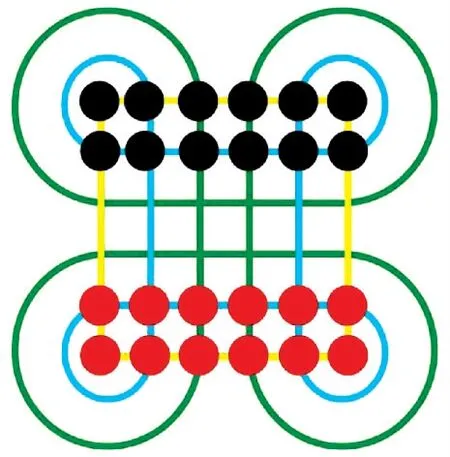
图1 苏拉卡尔塔棋盘、棋子以及开局布局Fig.1 Iayout of the Surakarta and Opening

在游戏开始时，双方轮流走棋，每次可以移动一个棋子或者吃掉对方的棋子。 当移动棋子时，只能沿垂直或者对角方向走动一格，并且在该位置上没有己方或者对方的棋子。 而当需要吃掉对方的棋子时，则需要经过至少一条完整的弧线，并且在我方棋子对对方棋子的路径上没有棋子阻碍。 游戏以吃掉对方棋子获取胜利，比赛结果以剩余棋子多的一方获胜。

2 基于蒙特卡洛树搜索的神经网络博弈方法

2.1 树搜索方法

通过使用蒙特卡洛方法，在树中对每一个棋局状态进行搜索。 随着模拟次数的增多，搜索树的深度和广度越来越大，并且对棋局的评估越来越接近实际情况。 因此，随着搜索时间的增多，选择具有高价值的子节点，算法选择的策略则越来越好。

神经网络为残差卷积神经网络fθ，其中θ 为神经网络的参数，输入值为当前对局的局面s，p 为将棋子移动到某个点的概率，值为0～1。v 是当前局面的评分，表示当前局面对我方的有利或不利程度，值为－1－－1， －1 表示输、1 表示赢。 表达形式如下：

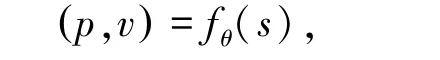
对于蒙特卡洛搜索树中的每一个节点，都存储了以下值；

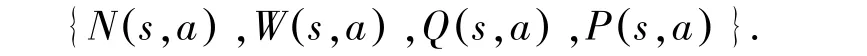
其中，N (s，a) 表示该节点的访问次数。W（s，a）表示评估值的总和。 Q（s，a） 表示评估值的平均。P（s，a） 表示在父亲节点来看选择该节点的概率值。蒙特卡洛树搜索通过以下步骤选择最优的下棋方法：

（1）选择

搜索开始时，要从根节点到达叶子节点。 在这个过程中，需要不断的选择搜索的节点，直到叶子节点。 当选择子节点时，通过PUCT 变种算法计算每个子节点的选择值［8］，并选择其中选择值最大的节点。

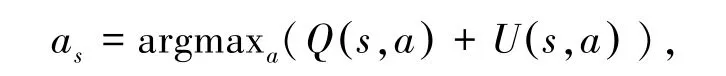
其中：

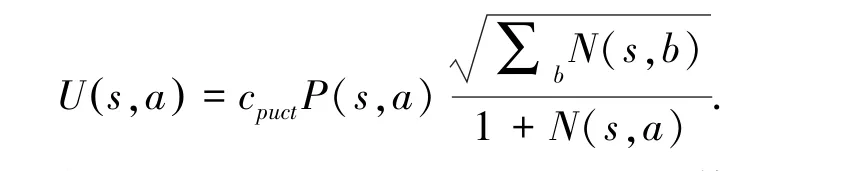
式中， Q (s，a) 表示对于子节点的评估的平均值；∑bN（s，b） 表示所有子节点访问次数的总和，即父节点的访问次数N（sp，ap），cpuct为一个常数；用于控制探索更多节点和利用已有信息的平衡。

（2）扩展和评估

当通过选择到达叶子节点时，对于局面s 通过神经网络进行前向推理获得p 和v。 对于可行域中的每一个可行动作a，新建对应的节点edge（s，a），值被初始化为｛N (s，a) ＝0，W (s，a) ＝0，Q (s，a) ＝0，P (s，a) ＝p｝，而对于v 将进行回溯更新。

（3）回溯更新

当叶子节点被扩展和评估后，将按照搜索树的选择自下而上对所有祖辈节点回溯更新，所有祖辈节点的访问次数均加一，即N (s，a) ＝N (s，a) ＋1。对于评估值的总和以及均值则根据行动方加v 或者－ v，即若当前的下棋方为评估局面方，则W (s，a) ＝W (s，a) ＋ v；若为评估局面方的对手方，则W (s，a) ＝W (s，a) － v。 同时均值也相应的更新为

（4）选择最优行动

经过多次选择、评估和扩展、回溯更新之后，则根据所有可行域的访问次数得到选择行动的概率其中， τ 为控制探索程度的温度参数，训练时τ ＝1，使得探索更多的可行域以提高探索程度；而当进行性能评估或对局时τ→0，尽可能获得更优的局面。

2.2 神经网络

与传统方法不同，机器学习方法并不需要特别的特征设计，只需要将棋盘数据和历史数据输入到网络中即可。 本文使用的输入特征见表1。 值得注意的是，与围棋不同，苏拉卡尔塔为移动型棋子，即把棋子从某一个位置移动到另外一个位置。 本文使用一个平面表示移动棋子的位置，用另一个平面表示棋子移动到的位置。 除此之外，使用了一个平面指示当前是否为先手方，若为先手方，则该平面全置为1，否则置为0。

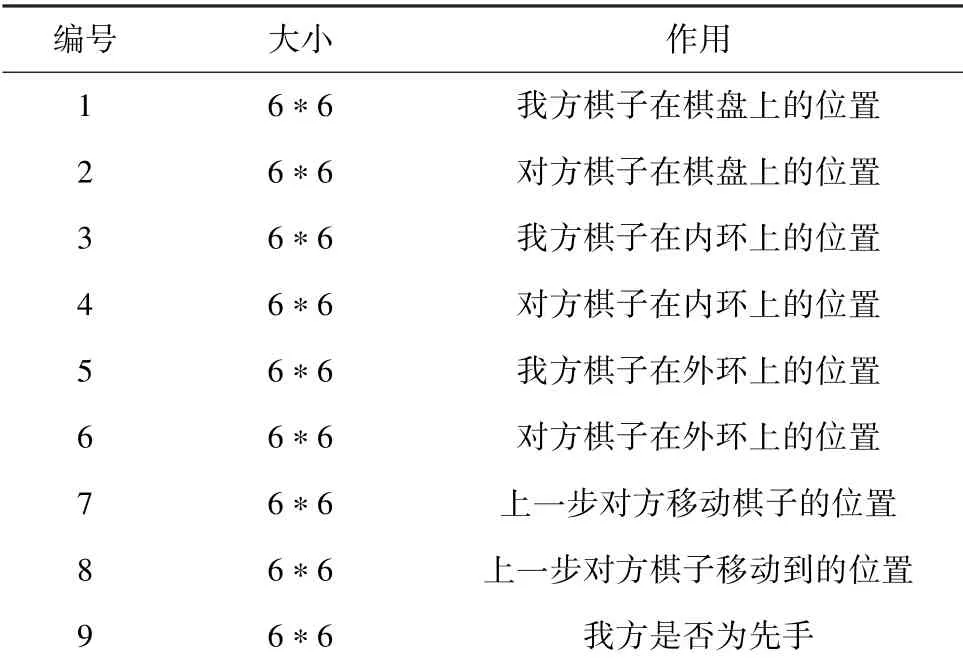
表1 输入特征Tab.1 Feature Representation

神经网络为6 层卷积残差网络，根据策略网络（见表2）和价值网络（见表3）分为2 个部分。 策略网络为36∗36 的输出，表示所有可行的移动。 价值网络为1 的神经元。

表2 策略网络Tab.2 Policy Network

表3 价值网络Tab.3 Value Network

随机初始化神经网络后，运用基于蒙特卡洛树搜索的神经网络方法进行自对弈，收集对弈数据（s，π，z）。 对于双方的历史棋局，结束时的棋局为sL，则对于所有历史局面sll ≤L， 得到选择行动的概率值π（a ｜sl）， 同时根据棋局最后的胜负结果，给予胜负值z ∈｛1，－1｝，即若当前方胜利z ＝1，否则z ＝－ 1。 为了防止过拟合［9］，程序将所有自对弈的历史放入到数据集中，当完成一定数量的自对弈后，则从数据集中采样一定数量的历史数据，通过反向传播算法对神经网络训练。 损失函数由交叉熵和平方差两部分组成，即对于某一历史：

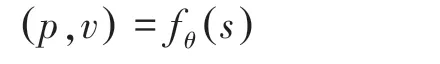
其中，c 为控制L2 正则化的参数。

2.3 并行训练方法

为了加快自对弈速度，本文使用了根并行方法［10］，如图2 所示。 当自对弈需要评估和扩展节点时，程序把当前局面发送到评估队列中，评估服务器按批进行前向推理并返回相应的自对弈程序。 当一局自对弈程序完成后，对弈程序将局历史发送到训练服务器，训练服务器维护一个训练数据集池，训练服务器将数据加入到数据集池后，从数据池中采样进行一次反向传播计算更新权重。 同时每1 min，训练服务器和评估服务器进行一次权重的同步，以保证评估服务器的权重是最新的。

图2 并行训练架构Fig.2 Architecture of Parallel Training

3 实验

为了检验实际训练效果，神经网络在训练和评估时，cpuct＝2；对于温度控制常量，训练时τ ＝1，性能评估时τ ＝0.1。 训练中，选择走子时仅进行了1 600次模拟。 而在评估性能时，应适当增加模拟次数，以获得更好的性能表现。 通过将训练560 局的神经网络与训练1 000局的神经网络进行100 局对战，双方均模拟30 s。 结果证明：1 000局训练后的神经网络胜率为60%。 由此可见，随着训练局数的增多，神经网络的水平逐渐提高，使用基于蒙特卡洛树搜索的神经网络博弈方法有助于提高苏拉卡尔塔程序的博弈水平。

4 结束语

本文将基于蒙特卡洛树搜索的神经网络博弈方法，应用于苏拉卡尔塔机器博弈中。 从零知识进行自学习的方案，能在五子棋、围棋等非移动型棋种上获得良好效果，但本文的实验不能证明其方法也适合于移动型棋子。 但经过自学习训练，程序的水平有明显的提高，可以断言，若自对弈上百万盘，程序的博弈水平必然有更好的提高。 在未来的研究实践中，还将在优化网络结构、调整自学习策略、引入人类对战数据等方面进行探索。