数学学业表现能力测评体系构建——中国义务教育质量监测的实践
2020-08-29王立东王烨晖史宁中宋乃庆刘晓玫
王立东,杨 涛,王烨晖,史宁中,宋乃庆,刘晓玫,马 复
数学学业表现能力测评体系构建——中国义务教育质量监测的实践
王立东1,杨 涛1,王烨晖1,史宁中2,宋乃庆3,4,刘晓玫5,马 复6
(1.北京师范大学 中国基础教育质量监测协同创新中心,北京 100875;2.东北师范大学 数学与统计学院,吉林 长春 130024;3.西南大学 基础教育研究中心,重庆 400715;4.中国基础教育质量监测协同创新中心西南大学分中心,重庆 400715;5.首都师范大学 教师教育学院,北京 100048;6.南京师范大学 教师教育学院,江苏 南京 210046)
从国家层面了解中国数学教育质量整体状况,有效地测量评价中国数学教育质量状况是中国义务教育质量监测工作的基本目标.基于2015—2018年两轮数学学科国家义务教育质量监测的实践,介绍了作为监测理论框架核心内容的数学表现能力指标体系.其中包括运算能力、空间能力、数据分析能力、推理能力和问题解决能力等多个表现能力维度.在此基础上,对于该指标体系的构建依据,命题原则及相应的监测结果做出述评.
数学学科;义务教育质量监测;表现能力指标;命题数学;数学表现
为贯彻党的十八大、十九大精神,落实《国家中长期教育改革和发展规划纲要(2010—2020年)》关于开展教育质量监测的有关要求,摸清作为中国未来发展和参与国际竞争最重要“家底”的中小学生的发展现状,进一步促进中国义务教育质量乃至基础教育质量的提升,根据《中华人民共和国义务教育法》和《国家义务教育质量监测方案》的相关规定,自2015年起,教育部基础教育质量监测中心(北京师范大学中国基础教育质量监测协同创新中心)在多年试点监测工作的基础上,正式在全国32个省、自治区、直辖市及新疆生产建设兵团范围内周期性地开展了义务教育质量监测工作.目前已完成2015—2017年第一周期[1]和2018年第二周期数学学科监测工作[2].
学业质量监测的有关研究是近年来得到学界广泛关注的主题[3].研究者基于教育部基础教育质量监测中心多年试点监测与两轮数学学科国家义务教育质量监测的理论设计与实践经验,向读者介绍作为监测理论框架核心内容的数学表现能力指标体系的构建依据,命题原则及相应的监测结果与政策启示等.
1 数学表现能力指标体系的构建
在设计教育质量监测的理论框架方面,学界提出了“五个统一”[4]的原则性要求,即,“现实性与前瞻性相统一、政策性和科学性相统一、全面性与指向性相统一、一般性和特殊性相统一、对代表性横断数据和纵向追踪数据均有显著预测力和规范性与实用性相统一”.在此基础上,构建数学学科监测的指标体系框架要考虑数学学科自身的特点,体现出数学学科与数学教育的本质要求.在关注学生数学基础知识和基本技能的掌握的基础上,同样要关注学生抽象能力、推理能力和创新能力的发展;还要反映出社会发展对个体素养的要求,引导学生主动建立数学世界与外部现实世界的联系,使学生充分发展提出问题、分析问题以及用数学思想和方法解决现实生活中问题的能力[5].
在数学监测的指标体系中,特别设置了表现能力指标体系,期望关注数学教育研究的前沿,结合中国数学教育的实际,在全面提高数学教育质量现状的要求下,指向数学教育的核心育人目标,在兼顾数学学科特殊性的同时,体现育人目标的一般性,期望监测结果能够为数学教育研究和数学教育政策实践提供实证基础.
1.1 数学学业表现能力指标体系的理论基础
注重能力导向的数学教学与评价已经形成学界共识[6],构建数学学科能力表现的指标体系框架,成为监测框架构建的核心问题.在有关指标体系的构建过程中,既基于中国数学教育研究相关的理论与实践成果,也参考借鉴了国际课程与大型测评项目的有关经验.
1.1.1 中国数学教育的研究传统
“能力立意”历来是中国数学教育培养目标的基本出发点之一.著名数学家华罗庚和关肇直于1958年提出:运算能力、逻辑思维能力和空间想象能力是数学的3种基本能力,这种阐述对中国的数学教育,尤其是培养学生的能力起了很大的作用[7].“我国数学教育的追求是:‘在良好的数学基础上谋求学生的数学发展.’这里的‘数学基础’,其内涵就是‘三大数学能力’;这里的‘数学发展’是指:提高用数学思想方法分析问题和解决问题的能力,促进学生在德智体各方面的全面发展.”[8]
随着社会与教育的进一步发展,对“三大能力”的片面强调,使得学校培养出来的学生虽然具有扎实的基础知识和技能、善于模仿、善于解常规题和竞赛题等优点,但学生的创造能力、动手能力、解决实际问题的能力相对较弱[9].对于数学能力结构的理解也得到了较大的拓展,呈现出多维化的特点.
有研究构建了基于“学习—应用—创新”的数学学科能力表现指标体系[3],包括数学学习理解能力、数学实践应用能力和数学创新迁移能力等问题解决倾向明显的能力维度.
中小学生的数学能力是一个多维度、多层次的结构系统.中小学生的数学能力可以分为两个层次.运算能力、空间想象能力、信息处理能力是第一个层次.以第一层次能力的获得为基础,学生会逐渐获得更高级的能力,理性思维方面会发展起逻辑思维能力,实践操作方面会发展起问题解决能力,这是第二个层次.而模式能力则在这两个层次之间起着非常重要的桥梁作用[10].
近年来,得到极大发展和政策应用的核心素养理论认为,核心素养是学生在接受相应学段教育过程中,逐步形成的适应个人终身发展和社会发展需要的必备品格与关键能力[11].数学核心素养是数学学习者在学习数学或学习数学某一个领域所应达成的综合性能力.数学核心素养是数学教学应当特别关注的基本素养[5].作为2015—2018年两轮数学学科义务教育质量监测理论设计依据的《义务教育数学课程标准(2011版)》明确提出10个核心素养,即数感、符号意识、空间观念、几何直观、数据分析观念、运算能力、推理能力、模型思想、应用意识和创新意识[12].10个核心素养既有内容维度,又有思维考量,这成为近年来中国数学教育课程设计与教学实践的基本依据.
1.1.2 国际课程与大型测评项目的经验借鉴
在各国的国家课程中,通常将数学能力的目标置于课程目标框架中十分核心的位置.例如,德国数学课程标准中的小学一般数学能力标准包括:解决问题能力、关联能力、数学论证能力、数学建模能力、数学描述能力;中学一般数学能力标准包括:数学论证、解决问题、数学建模、数学表征、数学符号、公式以及技巧的熟练掌握以及数学交流.英国国家数学课程规定了学生应掌握的3项数学能力,每个学段的每个不同领域的内容中都有一些标准是按问题解决、交流、推理3项基本能力划分的.美国数学教师协会在2000年《数学课程标准》提到6项能力,即,数的运算能力、问题解决的能力、逻辑推理能力、数学联结能力、数学交流能力和数学表示能力.
在国际大型测评项目中,也十分关注能力维度的测评.如PISA2012数学素养模型包括8项数学能力:交流,数学化,表述,推理和论证,设计问题解决策略,运用符号的、正式的、技术的语言,运算以及使用数学工具,细化了数学问题解决过程的方方面面.
依据上述考量,在国家义务教育质量监测的理论框架设计中,特别关注了学生数学学习的能力维度.数学表现能力维度作为数学学科国家义务教育质量监测的核心目标之一,用以刻画数学学科义务教育质量的现状,进而为后续的政策建议与质量提升提供依据.基于已有研究成果的启示、课程标准的要求以及监测工作的实际,在数学监测的理论框架体系中,监测专家团队构建了一个数学学业表现能力的指标体系框架,作为监测试题研制设计的基本蓝图.
1.2 数学学业表现能力指标体系的内涵
基于以上分析结果,来自全国不同地区的数学教育、数学课程、数学教研等领域的专家团队经过反复研讨、修订,达成共识:数学学业表现内涵及其测评指标的选取要充分体现义务教育的性质,突出数学教育促进学生发展,尤其是终身发展和适应未来社会发展的核心目标,突出数学的本质特征,关注公民核心素养,体现能力主线,充分发挥数学监测的导向作用.义务教育阶段学生数学学业表现是学生获得全面发展的基本素养,是学生未来生活、工作和学习的重要基础.数学学业表现是指学生经过一定阶段的数学学习后所获得的数学知识和技能,运用知识和技能解决问题的综合能力.
同时,由于国家监测的框架设计需要实现政策性和科学性相统一,既要服务于政策,又要来源于政策,还要遵循科学性的原则[1].开展国家数学教育质量测评,不仅要借鉴国际数学教育测评的经验,更要立足于中国数学教育的现实状况,体现国家数学教育目标,并对中国数学教育发展起到导向的作用.因此,在整个数学监测研发过程中,主要的依据包括:(1)国家教育方针政策相关规定,(2)《义务教育数学课程标准》的具体内容要求,(3)义务教育中小学十几套数学教材的深入分析比较结果.通过系统调研、访谈等方式,充分掌握中国数学教育教学发展的实际状况,尤其是地区差异状况,以及教育测量评价的基本理论和相关要求[3].
监测能力指标的框架设计首先以国家课程政策文件(《义务教育数学课程标准(2011版)》)的10个核心素养为基础.这是义务教育学业质量的基本目标.同时考虑到已有研究对于数学基本能力的深入讨论(能力的不同维度和不同层级),兼顾服务国家政策的需要(简明易懂,易于理论解释与政策应用).将核心素养进行分类整合提取,形成5个基本能力维度.
该框架选取的能力指标包括:运算能力、空间想象能力、数据分析能力、推理能力和问题解决能力(如图1).各指标的含义和作用如下.
(1)运算能力:主要是指学生能够根据法则和运算定律正确进行运算,并能理解计算的原理,寻求合理简捷运算途径的能力.兼顾核心素养中的数感、符号意识、运算能力等.
运算能力是学生数学思维能力发展的重要基础,是学生未来生活需要掌握的基本技能之一.
(2)空间想象能力:主要是指对空间图形的特征和关系进行认识,并利用图形描述和分析问题的能力.兼顾核心素养中的空间观念、几何直观等.
空间想象能力是人类基本智能形式之一,良好的空间想象能力是认知能力发展的重要体现,培养学生的空间想象能力能够帮助学生运用空间信息更好地描述、理解、分析和解决问题.
(3)数据分析能力:主要是指知道现实生活有许多问题应当先做调查研究,能够收集、整理和分析数据,能够从数据中提取信息并进行简单推断的能力.兼顾核心素养中的数据分析观念.
(4)推理能力:主要包括合情推理和演绎推理能力,合情推理主要指能从已有的事实出发,凭借经验和直觉,通过归纳和类比等过程推断某些结果;演绎推理主要指从已有事实(包括定义、公理、定理等)和确定的规则(包括运算的定义、法则、顺序等)出发,按照逻辑推理法则进行证明与计算.兼顾核心素养中的推理能力.
推理是数学的基本思维方式,是学生在学习和生活中必须学会和经常使用的思维方式;良好的推理能力有助于学生更好地获得新知识和新技能,并帮助他们解决生活中的各种问题.
(5)问题解决能力:主要是指学生凭借独立思考、创造性地运用所学知识和经验解决非常规问题的能力.兼顾核心素养中的模型思想、应用意识和创新意识等.
问题解决能力是学生创造性思维发展水平的重要体现,培养学生的问题解决能力有助于提升他们的创新意识和实践能力.
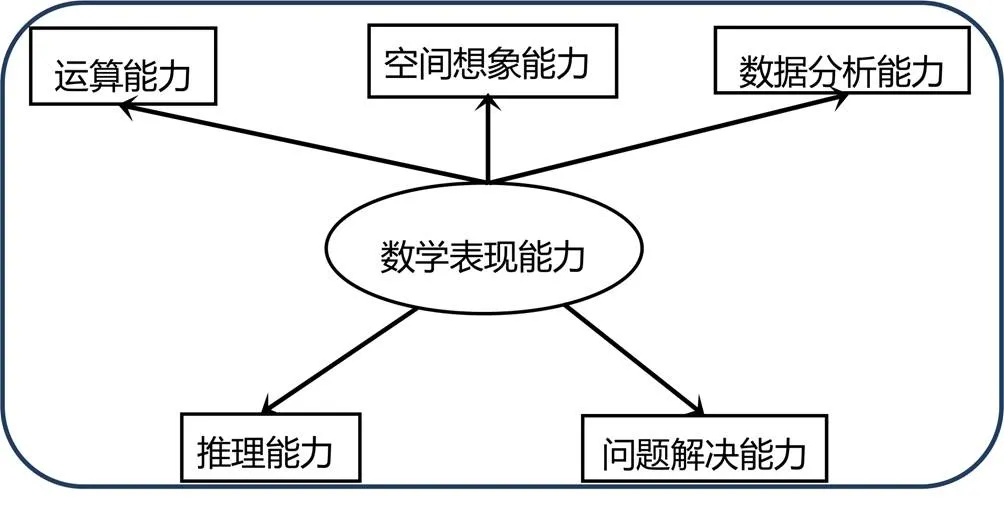
图1 中国义务教育质量监测数学能力指标体系框架
可以看到前3个基本能力涉及以数学学科的基本知识内容为载体,后2种能力涉及以数学学科的基本思维方式为载体,5个能力的指标体系较为全面地涵盖了数学核心素养的基本要求,符合数学学科育人的基本目标.
2 能力测评试题的命制
在特定的能力指标框架下,如何研发高质量的测试工具测评学生在5个能力指标上的表现,是义务教育质量监测工作的基本研究问题.
在两轮的数学监测工作中,结合多名专家意见,除了采用国际上通行的命题原则与命题方法之外,还提出了若干能力测评试题命题的原则与方法.
综上所述,我院行万古霉素血药浓度监测的ICU老年感染患者比例不高,且治疗有效率偏低;大部分患者的血药谷浓度不在有效范围内,且不同肾功能状况患者血药谷浓度的分布有所差异,肾功能异常患者的万古霉素血药浓度可能更高。临床上应重视老年重症感染患者血药浓度监测,并根据其血药谷浓度、肾功能指标等及时调整用药方案,实行个体化给药,以提高用药的有效性和安全性。但本研究的样本量略少,且患者数据收集路径过于单一,尚有待后续研究进一步完善。
2.1 试题与能力指标的关系——多能力指标试题
在能力指标体系及双向细目表的框架下,利用纸笔测验的方式考查学生在各个能力指标上的表现是大型教育测评中的基本做法.
从教育教学实践与命题实践可以看到,一道具有数学学科意义的数学试题的解答往往涉及多个内容相关能力或思维相关能力,而通常的教育测评要求将能力指标与试题实现一一对应,这种做法虽然在数据分析和学生能力水平估计上较为简单,但是与学生的实际心理认知过程不符,同时也丢失掉了部分题目信息,影响试题整体的效度.
基于上述考虑,结合多位专家意见,在2018年数学监测的试题研制指南中提出,每道题目所对应的具体能力指标可以设置两个能力要求.命题者在编码时需要设定权重,共有3种类型可选:100%—0%,75%—25%,50%—50%.
同时配套研发相应的多维项目反应理论的数据分析方法,以更好地估计学生在各能力水平上的表现.
2.2 能力测评试题的命题原则——以“问题解决”为例
对于学生问题解决能力的考查历来是教育测评的难点.特别是教育质量监测中以模型思想、应用意识和创新意识考查为目的的问题解决类题目的命制,更是需要系统的研究与实践作为基础的.
常规的数学问题在考查问题解决能力的功能上往往有限.问题不同于考题,好的问题具有启导性,诱发智力,不断提出新问题,甚至是无唯一解答的开放题.它反对“单纯模仿”,更多从问题情境出发,构造数学模型,提供数学想象,伴以实际操作,鼓励发散思想,诱发创造能力,把数学嵌入活的认知过程中去,而不是死的知识积累[13].
基于上述考虑,综合多位专家意见,在2018年数学监测的试题研制指南中提出,用于测量问题解决能力的试题宜单独命制,强调将数学学习理解能力、数学实践应用能力和数学创新迁移能力等思维层次的能力蕴含到问题解决能力当中,并结合第一轮监测的命题实践总结如下具体的、富有操作性的命题原则.
(1)问题解决测量的目标.对于未来数学教学的有所导向性,特别是学生创新能力培养.
(2)问题解决测试题目的基本特征.命题要求基于真实的情境(现实生活情境或者真实的科学问题情境,但不包括纯数学问题情境),需要学生对于情境有一个数学化的过程.试题应是非常规的,没有既定的模式,往往是(但不局限于)结构不良的、有冗余信息的问题.即使是达到课程标准所规定的学业目标的学生,也并非能够一目了然地、直接地解决问题,而需要有一个自己设计解题策略的数学思维的过程,而不是简单的回顾、模仿已有的数学问题(如教科书和教辅材料中的常见问题).问题解决命题基于数学知识,但要避免过于依赖具体数学知识,造成测量目标不够聚焦.问题解决问题测量功能聚焦.例如,2015年测试中,需要问题解决试题设计多个问题,其中第一问往往是常规问题,在本次命题中要规避这种形式.
(3)几种可能的问题类型(但不局限于这几个类型).可以考察要求学生说理的问题(应用数学结果决策,如统计决策、评价规则问题);可以考察要求学生基于给定信息材料“提出问题”“提出方案”的问题,但要考虑如何评价学生提出的问题、方案,或者要求学生提什么样的问题、方案(有难度的,有意义的,容易实施的);也可以考察包括要求学生基于给定信息材料提出数学猜想的问题;要求学生下定义的问题不作为问题解决问题.
3 首轮义务教育质量监测数学能力维度监测结果
2018年7月28日,教育部基础教育质量监测中心发布了首份中国义务教育质量监测报告.报告指出,首轮义务教育质量监测依据国家课程标准,对采用国际通用的程序和技术方法,将学业表现划分为4个水平段,分别是:待提高、中等、良好、优秀.监测结果显示,中小学生数学良好.四年级、八年级学生数学学业达到中等及以上水平的比例分别为84.6%、78.9%,达到优秀水平的比例分别为23.8%、26.7%.
学生数学学业5项能力上,四年级学生达到中等及以上水平的比例分别为运算能力(87.7%)、空间想象能力(82.2%)、数据分析能力(80.2%)、推理能力(82.3%)及问题解决能力(82.2%);八年级学生达到中等及以上水平的比例分别为运算能力(82.8%)、空间想象能力(78.7%)、数据分析能力(74.6%)、推理能力(78.5%)及问题解决能力(76.8%),如图2.
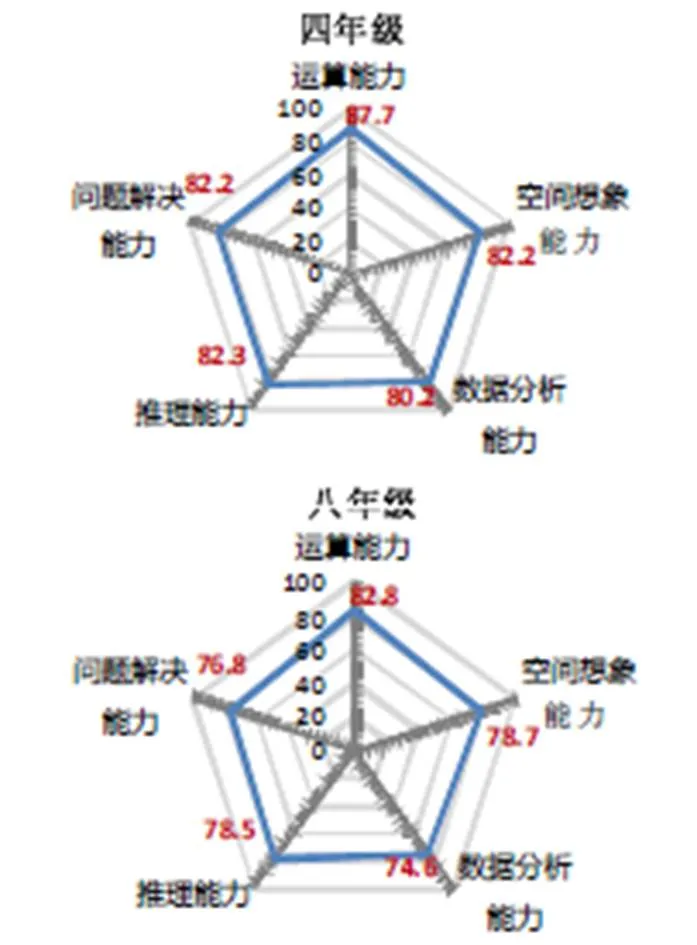
图2 四年级和八年级学生数学学业各项能力达到中等及以上水平的比例(%)
可以看到,按照课程标准的相关要求,四年级学生的运算能力水平较高,其它能力水平大体相当,这为后续的相关学习提供了很好的基础.八年级学生的数据分析能力相对于其它能力较弱,需要在课程政策与教学实践中加以关注,特别是在国家十分重视大数据的时代背景下.
特别值得关注的是,四年级、八年级学生均在问题解决能力方面取得了较好的成绩,结合以往有关研究[7,14],对于中国学生有关能力的担忧,可以看到,近年来,中国的数学教育工作者在培养学生提高多方面的数学能力上取得了重要的成绩,特别是在补齐“能力短板”方面有诸多建树.
监测同时包括对于32个省级行政区及新疆生产建设兵团的学生数学表现能力测评结果,可以为各省的数学教育教学政策的制定与质量提升提供依据.
4 结语
数学表现能力指标框架可以直接、高效地评价、监测学生的数学学习状况,进而反映中国数学教育质量的现状.
基于5项能力的数学教育质量监测实践过程建立了系统的监测工具研发,数据分析以及结果报告的规范化原则与流程,为后续“有效推进素质教育的落实,大力促进基础教育的均衡发展,切实实现教育行政与管理部门决策和管理的科学化、民主化和专业化,提高管理效能”[15]提供了重要的实证支撑.
[1] 教育部基础教育质量监测中心.中国义务教育质量监测报告[EB/OL].(2018-07-24)[2018-10-30].http://www. moe.gov.cn/jyb_xwfb/moe_1946/fj_2018/201807/P020180724685827455405.pdf.
[2] 王烨晖,张岳,杨涛,等.义务教育数学相关因素监测工具研发的探索与思考[J].数学教育学报,2018,27(5):12-16.
[3] 丁锐,盖晓松.东北地区某省会城市小学生数学学业质量监测报告[J].数学教育学报,2018,27(4):46-52.
[4] 李勉,张平平,罗良.中国义务教育质量关键影响因素监测框架——构建过程中应考虑的若干问题[J].北京师范大学学报(社会科学版),2017(2):37-44.
[5] 杨涛,辛涛,罗良,等.义务教育数学教育质量监测的探索与思考[J].数学教育学报,2018,27(5):1-7.
[6] 曹一鸣,刘晓婷,郭衎.数学学科能力及其表现研究[J].教育学报,2016,12(4):73-78.
[7] 孙宏安.数学能力新探[J].课程·教材·教法,1996,16(7):15-20.
[8] 张奠宙.关于中国数学教育的特色——与国际上相应概念的对照[J].人民教育,2010(2):36-38.
[9] 徐稼红.“三大能力”与“建模能力”[J].课程·教材·教法,1997,17(11):30-31.
[10] 史亚娟,华国栋.中小学生数学能力的结构及其培养[J].教育学报,2008,4(3):36-40.
[11] 辛涛,姜宇,林崇德,等.论学生发展核心素养的内涵特征及框架定位[J].中国教育学刊,2016(6):3-7.
[12] 中华人民共和国教育部.义务教育数学课程标准(2011年版)[M].北京:北京师范大学出版社,2011:1.
[13] 张奠宙.数学教育改革的十个问题[J].学科教育,1993(3):12-15.
[14] 蔡金法.中美学生数学学习的系列实证研究:他山之石,何以攻玉[M].北京:教育科学出版社,2007:1.
[15] 董奇.构建具有中国特色的基础教育质量监测体系[J].人民教育,2007(Z2):2-3.
Constructing an Assessment Framework of Mathematical Performance in China National Assessment of Education Quality
WANG Li-dong1, YANG Tao1,WANG Ye-hui1, SHI Ning-zhong2, SONG Nai-qing3, 4, LIU Xiao-mei5, MA Fu6
(1. Collaborative Innovation Center of Assessment of Basic Education Quality, Beijing Normal University, Beijing 100875, China;2. School of Mathematics and Statistics, Northeast Normal University, Jilin Changchun 130024, China;3. Research Center of Basic Education, Southwest Normal University, Chongqing 400715, China;4. Sub-Center of Southwest Normal University of National Innovation of Basic Education Quality Assessment center, Chongqing 400715, China;5. Faculty of Teacher Education, Capital Normal University, Beijing 100037, China;6. Teacher Education College, Nanjing Normal University, Jiangsu Nanjing 210046, China)
At the national level, the basic goal of the National Assessment of Education Quality is to understand the overall quality of national mathematics education as well as to effectively assess and evaluate the quality of national mathematics education. Based on two rounds of the National Assessment of Education Quality-Mathematics from 2015 to 2018, this paper introduces a framework of evaluating students’ performance in mathematics, which is the core content area. It includes computation, spatial visualization, data analysis and interpretation, reasoning, and problem solving. We describe how the theoretical framework was constructed for item development and also report on students’ performance in mathematics.
mathematics; National Assessment of Education Quality; performance indicators; mathematical item development; mathematical performance
2020–03–12
王立东(1983—),男,黑龙江哈尔滨人,博士,主要从事为数学教学论、教育测量评价研究.
G622.4
A
1004–9894(2020)04–0058–04
王立东,杨涛,王烨晖,等.数学学业表现能力测评体系构建——中国义务教育质量监测的实践[J].数学教育学报,2020,29(4):58-61.
[责任编校:陈汉君、陈隽]
