小学四年级学生数学情境问题解决能力调查研究——以湖南省为例
2020-08-29邓海英魏亚楠
邓海英,魏亚楠,严 卿
小学四年级学生数学情境问题解决能力调查研究——以湖南省为例
邓海英1,魏亚楠2,严 卿3
(1.湖南第一师范学院 数学与计算科学学院,湖南 长沙 410205;2.南京师范大学 数学科学学院,江苏 南京 210023;3.南京师范大学 课程与教学研究所,江苏 南京 210097)
数学情境问题解决指学习者从情境中抽象出数学问题并分析、解决问题的过程.解决情境问题的水平按照由低到高分为知识理解、知识迁移和知识创新3个层次.调查表明:(1)湖南地区小学四年级学生解决数学情境问题属于偏低水平.(2)性别对数学情境问题的解决能力没有显著差异.(3)城市与农村学生数学情境问题解决能力存在显著差异.(4)学习成绩与数学情境问题解决能力密切相关,其中知识迁移的作用至关重要.
小学四年级学生;数学情境;问题解决
1 问题提出
《义务教育数学课程标准(2011年版)》提出了“十大核心词”:数感、符号意识、空间观念、几何直观、数据分析观念、运算能力、推理能力、模型思想、应用意识和创新意识,引发了数学基础教育的变革.随后又颁布了《普通高中数学课程标准(2017年版)》并提出六大数学核心素养(数学抽象、逻辑推理、数学建模、数学运算、直观想象和数据分析),势必对小学数学教育教学产生新的启示,对小学数学核心素养的培育必然产生新的要求.在国际上,研究数学核心素养培育的一个重要视角就是与情境的结合[1].大型国际教育测评项目PISA在数学素养测评中一直特别关注学生“在各种现实情境中表达、运用和解释数学的个人能力”[2],特别关注数学情境和问题之间的关联[3].国内有学者认为要在数学教学活动中创设合适的教学情境形成和发展数学核心素养[4],国外亦有研究者认为数学核心素养要借助特定情境潜移默化习得[5].这些有关现实情境与数学核心素养的认识对小学阶段也具有启发性:在小学数学教学中,也要重视解决现实情境问题的能力培养,以促进学生核心素养的发展,但是这方面的理论和实证研究目前都非常缺乏.
解决数学情境问题本质上也是一种情境学习,基于PISA理念它更倾向于以弗赖登塔尔为主要代表的现实数学教育.有关现实情境对数学学习的促进作用,已有不少论述:如20世纪90年代西方情境学习理论认为学习是在情境中发生的;有利于学习发生的情境是一种真实的社会情境、实践情境和文化情境[6];数学情境(包含现实情境)是校外数学走向学校数学的中介,并在此过程中起着导向功能[7].在实践层面,2000年,全美数学教师联合会(NCTM)在《学校数学的原则与标准》中提出了“教师要有计划地要求学生依据各种数学情境提出自己感兴趣的数学问题,包括数学内部和外部问题”的要求[8],之后有专家学者开始聚焦如何评价学生在现实情境中提出问题的创新能力.同年,在中国,吕传汉等提出了“以数学情境为基础,以数学问题为纽带的启发式教学”的数学“情境—问题”教学基本模式[9],由此带动了情境在数学教学设计中的运用,拉开了情境教学改革的大幕,以培养学生提出问题、解决问题和创造创新的能力[10–11].但是,也有研究发现,经过正规教育的儿童,在解决需要考虑现实情境或现实意义才能正确解决的问题时,却存在着严重忽视现实情境的倾向[12].由此,不得不引发如下的思考:在提倡数学核心素养的今天,在PISA数学素养理念之下,小学生解决情境问题的水平如何?怎样评价?为了探讨这些问题,依据朱智贤、林崇德等一批心理学者的研究结论(小学三~四年级是儿童思维独创性、深刻性发展的转折点,是初步本质抽象概括能力发展的关键时期[13],这些能力也是中小学数学核心素养的关键成分),选择湖南省部分城区和农村的四年级小学生为调查对象,测试分析数学情境问题解决水平,探索不同性别、不同地区学生情境问题解决能力的差异、情境问题解决与学业成绩的关系,情境问题解决的影响因素等.
2 研究设计
2.1 工具的基本结构与水平划分
喻平主张知识是学科关键能力生成的本源,认为知识学习的3种形态(知识理解、知识迁移和知识创新)是学科关键能力的生成机制,进而生成学科关键能力的一、二、三级水平[14],认为要发展学生的数学核心素养,就要发展学生的关键能力[15].由此,提出了一个数学核心素养评价的框架,该框架将关键能力的生成分为知识理解、知识迁移和知识创新3个阶段.情境问题解决同样是一种数学能力,知识也是情境问题解决能力生成的本源,需要理解知识、创造性地运用知识.因此测试借鉴该框架,将总量表分成知识理解、知识迁移、知识创新3个维度.这里参照PISA的情境分类,将情境分为个人情境、教育或职业情境、公共情境、科学情境[16].个人情境指与学生个人的日常活动直接相关的情境;教育或职业的情境指与学生的学校生活或工作环境相关的情境;公共情境指与学生周边更广泛的环境相关的情境;科学情境指与技术过程、理论情境或明确的数学问题有关的情境.
测试卷由数学教育专业教授、研究生和小学数学特级教师共同编制完成,包括9道大题共13小题.数学关键能力三级水平的描述、测试卷基本结构及样题见表1.

表1 数学情境问题解决的三级水平与试卷的结构对应
2.2 工具的指标分析
在湖南省随机选取了190名四年级学生进行预测,男生108人,女生82人,试卷回收后使用SPSS17.0进行统计分析,结果如下.
(1)题项分析.依据总分高低将样本分为3组,每组各占总人数的约三分之一,高分组为总分大于等于59分的样本,共60人;低分组为总分小于等于33分的样本,共56人.对高、低组样本在每个题项上做独立样本检验,规定显著性水平为0.01.结果表明所有题项差异均达到显著水平.其次,计算得到每个题项得分与总分的相关系数都大于0.2,且都在0.001的显著水平上相关,说明题项与测验卷总分有较好的相关性,因此保留所有题项.
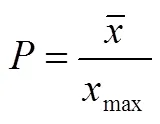
(3)信度检验.测试卷划分为知识理解、知识迁移、知识创新3个水平,计算得到3个水平内部及测试总分的克伦巴赫系数分别为0.725、0.568、0.555、0.799.总测验的内部一致性系数为0.799,说明该测验总体的信度是可以接受的.
(4)效度检验.计算3个水平及总测验得分间的相关系数,结果见表2.
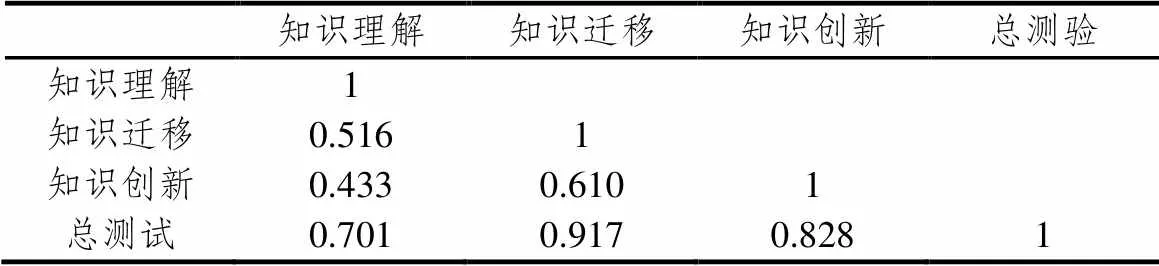
表2 测试卷结构效度分析
3个水平之间的相关系数小于每个水平与总量表的相关系数,表明该测验卷具有较好的结构效度.同时,知识理解和知识创新之间的相关系数小于知识理解与知识迁移,同时也小于知识迁移与知识创新,说明3个水平的层次划分合理.
2.3 被试选择
随机选取湖南省长沙市两个城区4所学校,湖南省郴州地区两个县4所学校(视为该测试农村地区学生样本),这些地区、学校在经济水平和办学质量上层次不同,具有一定的代表性.根据学校办学规模不同,选取班级有两种情况:学校四年级班级总个数为3个以内的,全选,若为10个的则随机选取4个.具体情况为:随机选取湖南省长沙市A城区实验小学4个班,长沙市B城区两所学校3个班和一所学校两个班,湖南省郴州地区C县县中心完小4个班,郴州地区D县一所乡镇小学两个班和一所乡村小学一个班,共8所学校17个班级,下发814份试卷对四年级学生进行正式测验.测试卷收回后,除去白卷(无作答且无记名,视为自动放弃测试或缺考或余卷),得到有效试卷800份,其中男生415人,女生385人,湖南省城区学生415人,农村地区学生385人.所得数据用SPSS17.0进行处理.
3 调查结果
3.1 数学情境问题解决的总体情况
表3显示,此次测验知识理解、知识迁移、知识创新和总测试平均得分分别为16.23、15.36、3.76和35.35,样本统计到最高分98、最低分0.以60分作为及格水平,对各水平得分做单样本检验,3个水平的检验值分别定为28×0.6=16.8≈17,41×0.6=24.6≈25,31×0.6=18.6≈19,测验总分的检验值定为60,分别对3个水平以及总分作单个总体检验.结果见表4.
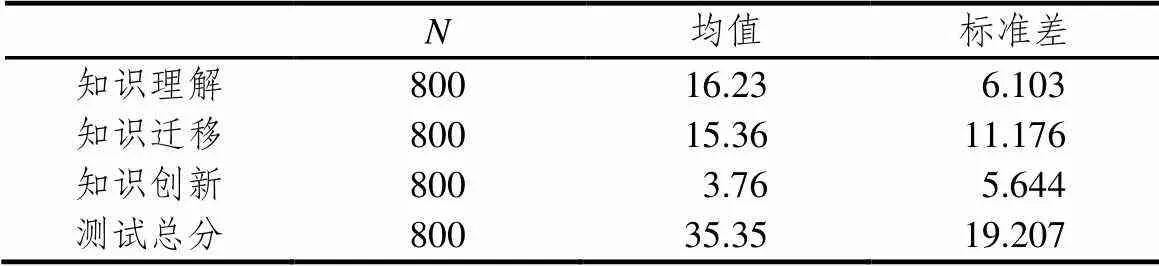
表3 基本统计数据

表4 单个样本检验
分析得知,(1)总测验<0.01,说明样本不是来自均分为60的总体,样本的实际均分为35.35<60,整体而言湖南地区小学四年级学生的数学情境问题解决的能力低于及格水平.(2)知识理解水平<0.01,说明样本不是来自均分为17的总体,样本的实际均分为16.23<17,整体而言湖南地区小学四年级学生接近知识理解的及格水平.(3)知识迁移水平<0.01,说明样本不是来自均分为25的总体,样本的实际均分为15.36<25,整体而言,湖南地区小学四年级学生低于知识迁移的及格水平.(4)知识创新水平<0.01,说明样本不是来自均分为19的总体,样本的实际均分为3.76<19,整体而言,湖南地区小学四年级学生远未达到知识创新的及格水平.
3.2 数学情境问题解决的性别差异
对男女生得分进行独立样本检验,女生得分在各水平及总分上都略高于男生,但差异均没有达到显著水平.结果见表5.
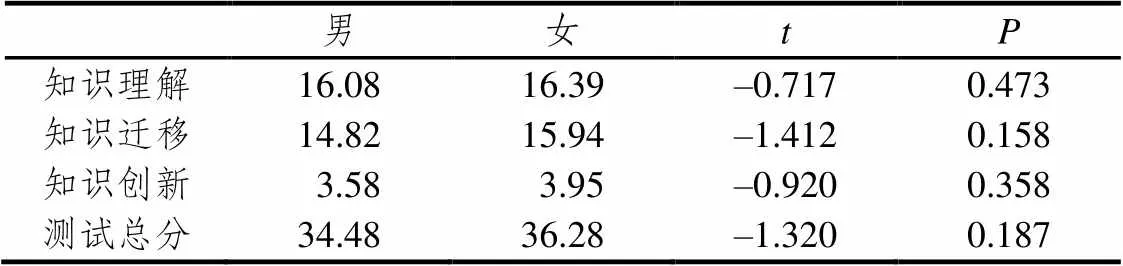
表5 男女学生测试得分检验
3.3 数学情境问题解决的区域差异
对农村和城市两个区域做独立样本检验,结果显示农村地区和城市地区在3个水平和测试总分上都存在着显著差异.结果见表6.
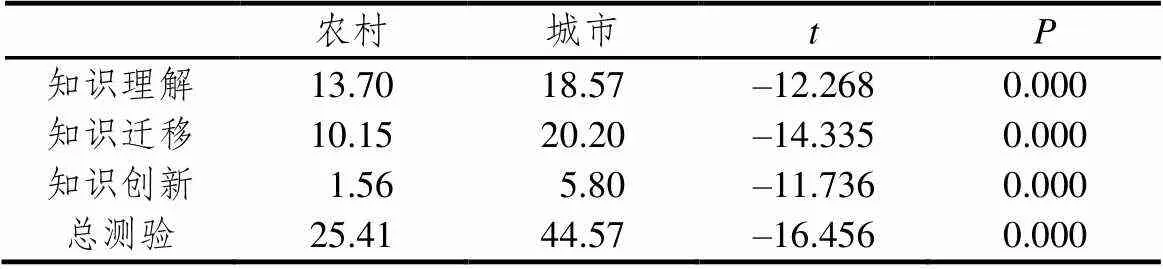
表6 区域比较
3.4 数学情境问题解决与学业成绩的相关性
为了分析数学情境问题解决的三级水平及测试总分与被试的学业成绩是否有关联,在17个班级中选取了长沙市B城区3所小学5个班的200名学生,并调取他们四年级第二学期期末考试成绩(注:3所学校位于同一个区,使用统一的教材,四年级的期末考试内容基本接近或相同,考试难度适中,若年级考试成绩优秀比例为40%,则优秀分数线一般在93分左右),结果见表7,并进一步做相关度分析,得到表8.
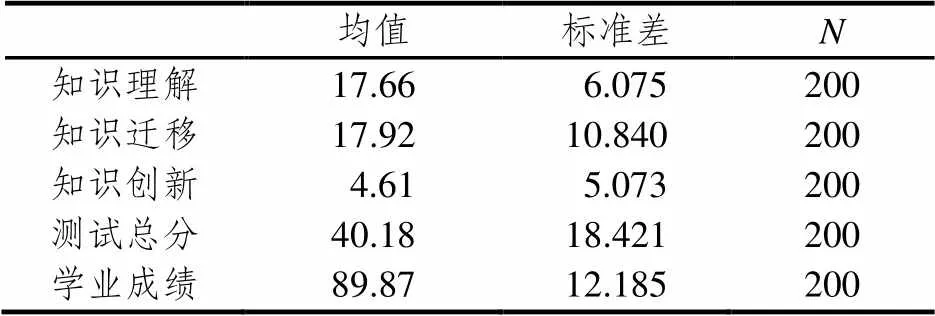
表7 描述性统计量

表8 数学情境问题解决能力与学业成绩的相关矩阵
从表7看出,这200名被试的期末考试平均成绩为89.87分,分数中等偏上.由表8看出,知识理解、知识迁移、知识创新3个维度、测试总分与学业成绩的相关系数分别为0.424、0.504、0.333、0.528,在显著水平为0.01时(双尾),结果显示3个维度、测试总分与学业成绩呈显著相关,在3个维度中,知识迁移与学业成绩的相关度最高.
3.5 数学情境问题解决能力与数学学习兴趣及解题策略和元认知的相关性
为了进一步研究数学情境问题解决能力的影响因素,编制了包括数学学习兴趣(总分20分)、解题策略(总分20分)、元认知(总分16分)3个维度(总分56分)的调查问卷,此外问卷还包括了6道其它的题(总分24分),用来调查学生对试题难易程度等的看法.在测试的800份样本中,去掉调查问卷漏答、答案规律明显(如全部选非常符合但试卷得分又极低)、白卷等废卷,共获得622份有效答卷.学习兴趣、解题策略、元认知与测试总分的相关性结果如表9所示.
从表9看出,学生在数学学习兴趣、解题策略、元认知3个维度上的总分平均得分为36.71分,优于情境问题测试得分.从表10看出,数学学习兴趣、解题策略、元认知与测试总分的相关度分别为0.244、0.152、0.203,学习兴趣与测试总分的关联度居3个维度之首,元认知次之,解题策略位居第三.
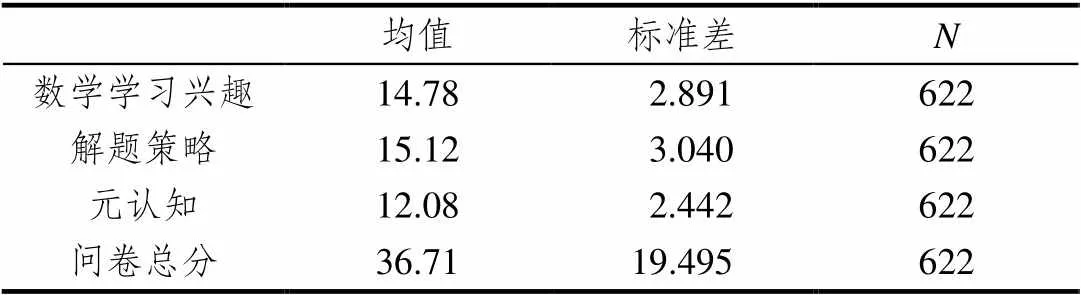
表9 描述性统计量
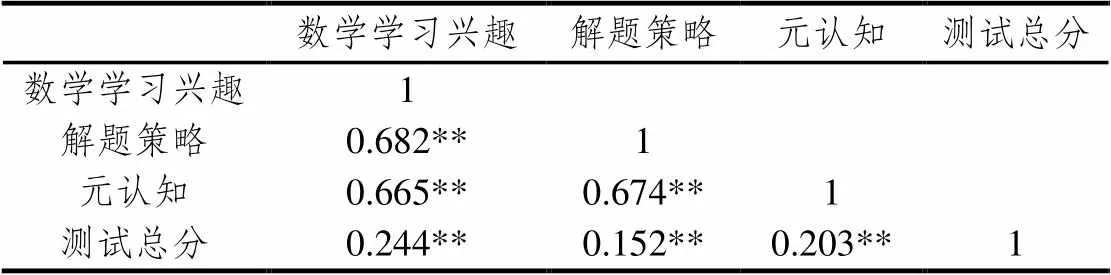
表10 相关矩阵
4 结论
综合以上调查结果,以湖南省为例,小学四年级学生数学情境问题解决水平总体偏低,尤其是知识迁移和知识创新水平均没有达到及格标准,知识理解水平接近及格标准.性别对数学情境问题的解决能力没有显著差异;城市与农村学生数学情境问题解决能力存在显著差异;学习成绩与数学情境问题解决能力密切相关,其中知识迁移的作用至关重要.数学学习兴趣、解题策略、元认知也与数学情境问题解决能力关系密切,学习兴趣是其中相关度最大的因素.
5 讨论
5.1 学校教育是数学情境问题解决能力的客观影响因素
测试结果显示,被试在数学情境问题解决中,知识理解的水平和稳定性都高于知识迁移和知识创新的水平和稳定性,这与中国重视“双基”的学校教育是分不开的,夯实了学生的知识基础,在情境问题解决中也能较好地运用相关基础知识;但是测试也显示,被试数学情境问题解决中迁移和创新能力都普遍偏弱,这与中国小学数学教育长期不够重视学生数学活动经验、数学思想方法等的培养也有很大关系.可见,学校教育是影响学生数学情境问题解决能力培养的重要客观因素.
5.2 数学情境问题解决中知识迁移起着决定性作用
当代认知心理学派认为“学习是一种迁移”.数学情境问题解决中的知识迁移是结合各种具体情境的高水平的迁移,调查显示这种迁移能力的高低在数学情境问题解决中具有很大的影响力.在表8中,数学情境问题解决能力与学业成绩密切相关,知识迁移是最大的相关因素.在表3、表7中知识迁移的标准差也都超过知识理解和知识创新的标准差,更接近测试总分的标准差,一方面说明知识迁移水平是被试知识理解、知识迁移、知识创新3个水平中最参差不齐的,另一方面说明被试知识迁移水平的稳定程度对被试测试总分的稳定程度影响最大.又如表5中知识迁移的值小于知识理解和知识创新的值,说明尽管男女学生在测试总分不存在显著性别差异,但是男女学生在数学情境问题解决中,知识迁移的性别差异要大于知识理解和知识创新的性别差异,更接近测试总分的性别差异.由此看到,在数学情境问题解决中,知识迁移对测试总体水平的高低以及稳定性起着决定性作用.
5.3 数学学习兴趣和元认知及解题策略是数学情境问题解决重要的内部因素
湖南A城区实验小学某教师在接受访谈时提到:学生平日很少接触与测试题类似的题型,只有部分参加数学竞赛的学生会有练习,或者平日善于总结、归纳的学生才善于解决这样的题型.这就涉及到解题策略和元认知的问题,实际上,表10的数据也显示,数学学习兴趣、元认知、解题策略两两之间呈中度相关,3者联系在一起,共同影响数学情境问题解决能力.通过分析调查问卷也发现:部分测试成绩很好的学生体现了较高的数学学习兴趣,如喜欢解答数学题、在课外有数学阅读、会做一些竞赛题等;会采取一些较好的解题策略,如在读题时先找关键词和数量关系、答完题后会检查一遍是否正确等;还能较好地监控自己的解题行为,在遇到障碍时会做出调节,做完题后会反思等,表现出较好的元认知水平.而测试不好的学生在这些方面都有所不足,尤其害怕困难,容易放弃,不敢尝试,缺乏信心.从表10的数据进一步看出,数学学习兴趣与测试总分的关联度居3个维度之首,元认知次之,解题策略位居第三.说明在此次陌生的测试题型面前,数学学习兴趣是答题的第一驱动力,而元认知一旦形成,则具备较好的稳定性,不会轻易随试题类型、难度等外部条件的变化而变化;而惯有的解题策略是否有效,会受到试题类型、难度等外部条件的影响,稳定性不及元认知.因此,元认知能表现出比解题策略与测试总分更高的相关度,也说明被试以往的解题策略在此次测试题的诸多“情境”中失效严重.
调查发现,影响数学情境问题解决能力的因素是多方面的,影响程度也各有不同,如情境类型、情境熟悉度、认知负荷等,在另文中有讨论.
6 启示与建议
(1)学校教育应重视数学情境问题解决教学,缩小地区差异,促进学生发展.
学校重视数学情境问题解决教学,包括以下4个方面.① 要意识到在现实情境中解决问题是一种高水平的数学能力,是学生数学核心素养的良好体现,如何培养这种能力也是当前国际教育研究关注的焦点,学校教育也要与时俱进,力争与国际接轨.② 培养学生解决情境问题的能力,与中国的“四基”教育并不矛盾.由表8的相关性可以看出,这种能力的高低可以很好地成为学生学业成绩好坏的风向标,提高学生数学情境问题解决能力,也能提高学生的学习成绩,提升学校教学质量.③ 学校应认识到在数学情境问题解决能力上,男女学生不存在性别差异.实际上,早在PISA2012的测试结果也显示了21个国家或地区学生数学素养无性别差异[17],中国相关研究也发现无性别差异[18].由此得到启示:在四年级这个关键的思维发展时期,男女学生在数学情境问题解决能力方面是在同一水平线上的.所以,外界不能对学生的数学学习带有性别歧视,尤其是教师,不能对学生性别先入为主的区别对待,而应平等相待.④ 学校要看到以下现象:由于当地社会文化背景、经济发展水平[19–20]等的影响或条件约束,不同地区、不同学校之间在教学理念、教学质量等方面存在一定的差异.情境问题解决能力与核心素养关系密切,而中国正在不断深入的核心素养教育改革,也出现了明显的地区差异:一方面经济发达地区的学校已经走在了改革的前列,出现了核心素养教育改革“强省”“强校”,一方面却有不少学校因为地理位置偏僻、办学条件较差、师资力量薄弱等原因尚未开展教学改革或者改革进展相当缓慢,显得教学理念滞后,教学水平落后,跟不上改革的步伐.因此,不同学校、不同地区之间要克服困难、创造条件加强教学交流,分享和学习好经验,以“强”扶“弱”,以“先”带“后”,减少地区差异,促进学生发展.
(2)加强数学概念与现实情境的关联,促进解题策略的正迁移.
从认知心理学角度分析,数学问题解决就是解题者在元认知调控下,对问题进行表征,对问题进行模式识别,然后在自己的长时记忆中提取解题图式(包括个体已有的与新问题有关的知识基础、解题策略、解题经验)并迁移至新的问题情境,进而达到目标状态的信息加工行为[21].解题者能根据问题情境有效地选择解题策略是解决问题的关键.而四年级小学生在面对陌生的现实情境时,正是缺乏正确选择解题策略的能力.此次测试结果表明了这一点:被试普遍偏低的测试总分和他们中等偏上的学校期末考试成绩不太相称,说明学生在常规的学校数学学习中获得的多种解题策略,在遇到此次情境问题时失效严重.表10的数据反应了这个现象:解题策略与测试总分的相关性低于数学兴趣和元认知与测试总分的相关性,这并不说明解题策略在数学情境问题解决中不重要,而是说明了解题策略在这次测试中作用发挥不明显.其中最大的原因,就是问题中现实情境的设计,因为情境本身既有外显的表征方式,也内隐了它所联系的数学概念、运算、推理等,从而增加了有现实背景问题的难度[22],这个难度不一定是问题本身的难度,而是问题解决的难度,它的本质是表征复杂性[23].比如一个问题本身所涉及的知识非常基础,几乎没有难度,但是置于现实情境之后,由于情境的干扰使得解决这个问题的过程变难,那么解题者在提取解题图式的每一个成分时都会变难.此外,在现行核心素养理念下,解决情境问题往往需要结合现实情境进行推理、运算、分析数据、建立模型,需要有强烈的数感、清晰的空间观念、很好的应用意识和创新意识等,这种更高要求的解题过程本身也增加了解决数学情境问题的难度,这些难度都会直接影响解题者解题策略的选择和迁移.
要克服这些因为引入情境而使“关系变得复杂”带来的难度,首要任务就是要在平日的学习中加强数学概念与现实情境的关联,将数学概念与它在现实世界中的“现实原型”联系起来.比如此次测试题1“登富士山”的公共情境问题:“每年的7月1号到7月30号富士山对公众开放,在这段时间里,大约有9 000名游客去富士山爬山,平均每天大约有名游客.”这道题目需要学生将“平均数”的概念与登山情境中“平均每天登山人数”这一现实原型建立对应关系, “9 000名”对应“总数”,1号到30号之间有“30天”对应“平均分成的份数”,完成这些关系对应之后,求平均数的解题策略“9 000÷30=300”也顺利迁移.又如表1中的试卷第9题,根据题意可以设计“等待红灯”为增加的条件.被试在这样新创设的情境中,将数学公式中的“路程”“速度”“时间”与题中的“千米数”、高速限速、实际车速、到办公室需要的时间进行对应,从而将“路程÷速度=时间”的解题策略迁移至问题情境.这道题相比题1,“时间”的现实原型稍显多样化,不但要分数段将开车行驶的时间相加,还要加上等待红灯的时间才能等于“到办公室需要的时间”.由此,关联数学概念与现实情境也是有层次性的.当然,现实原型与数学模式之间也有许多关系不明确[24],如表1中试卷第5题的科学情境,学生很难找到“数组”的现实原型,而只有仔细观察、比较、概括、归纳数据的异同,做出判断、解决问题、再进行检验等.但是,总体来看,在解决情境问题时,先找出数学概念与现实情境中“量”的对应关系,是明确解题策略的好方法.
(3)关注现实情境,明确问题指向,突出问题解决.
基于PISA和核心素养的共同理念,现实情境对培养学生的数学素养和关键能力具有积极的作用.数学情境问题解决中的情境设计,不是通过情境创设学习一个概念、一个规则,而是要突出问题解决,要有明确的问题指向,最终要在情境中解决问题.在实际教学中,中小学教师易倾向于选择一些数学故事、游戏、数学史等素材设计情境,并且还不乏有教师对情境的创设和运用多是拿来主义,既不理解为什么要引入情境,也不理解情境创设是否有效,尤其缺乏针对某一学科的情境设计[25];在数学教学中,情境的使用少有教师会深入到问题解决的内部.为了突出问题解决,可以参考前文中提到的四大现实情境分类(个人情境、教育或职业情境、公共情境、科学情境)进行情境创设,再进一步让学生经历“数学化”过程(包括3个方面:懂得表征问题情境为数学问题,会运用数学概念、事实、程序和推理,阐释、运用、评估数学结果到现实情境[26]),引导学生解决问题.以表1中的试卷第4题公共情境为例,教师在“两点间距离知识”教学中应当注意到在现实世界中3个实体建筑间距离的复杂性与多样化,可以让学生利用课余时间在合适的公共场合下切身体会3个实体建筑两两之间的距离关系,也可以在教室里模拟,再从中抽象出数学问题,感受数学问题的生成过程,感受数学发现的拟真过程,运用相关知识解决问题并结合情境进行评估和反思.就公共情境的创设而言,不一定要把“超市、体育中心、学校”“搬”到PPT和电脑屏幕上,只要能准确反映数学问题,让学生明确问题目标,可以采取灵活多样、生活化的方式进行.由于四大现实情境的复杂性,各种情境创设的要点各有不同,但创设现实情境的宗旨是一样的:让学生“重”在体验情境,“贵”在感知情境与数学的关联,“深”在认清情境之下问题的本质,“活”在能够正确迁移,最终提高数学情境问题解决能力.
[1] 常磊,鲍建生.情境视角下的数学核心素养[J].数学教育学报,2017,26(2):24–28.
[2] 陈敏,杨玉东.小学生解决真实情境问题的调查研究——基于PISA数学素养的视角[J].上海教育科研,2016(9):46–49,54.
[3] 周慧,綦春霞.PISA2012数学素养测试分析框架及例题分析[J].教育测量与评价(理论版),2015(5):36–42.
[4] 史宁中.试论数学推理过程的逻辑性——兼论什么是有逻辑的推理[J].数学教育学报,2016,25(4):1–16.
[5] LENGNIK. Reflecting mathematics: An approach to achieve mathematical literacy [J]. Zdm the International Journal on Mathematics Education, 2005, 37 (3): 246–249.
[6] 崔允漷,王中男.学习如何发生:情境学习理论的诠释[J].教育科学研究,2012(7):28–32.
[7] 曹新,纪雪颖,张永雪.对数学情境及其性质、作用的探讨[J].课程·教材·教法,2011,31(1):89–94.
[8] National Council of Teachers of Mathematics (NCTM). Principles and standards for school mathematics [M]. Reston, Va: NCTM, 2000: 258.
[9] 汪秉彝,吕传汉.创新与中小学数学教育[J].数学教育学报,2000,9(4):34–37.
[10] 吕传汉,汪秉彝.论中小学“数学情境与提出问题”的数学学习[J].数学教育学报,2001,10(4):9–14.
[11] 吕传汉,汪秉彝.再论中小学“数学情境与提出问题”的数学学习[J].数学教育学报,2002,11(4):72–76.
[12] 张丽,辛自强.简论数学现实性问题解决能力[J].上海教育科研,2005(1):56–58.
[13] 林崇德.智力发展与数学学习[M].北京:中国轻工业出版社,2011:185.
[14] 喻平.数学核心素养评价的一个框架[J].数学教育学报,2017,26(2):19–23,59.
[15] 喻平.发展学生学科核心素养的教学目标与策略[J].课程·教材·教法,2017,37(1):48–53,68.
[16] 陈慧,袁珠.PISA:一个国际性的学生评价项目[J].外国中小学教育,2008(8):53–58.
[17] OECD. PISA2012 assessment and analytical frame-work, mathematics, reading, science, problem solving and financial literacy [M]. Paris: OECD Publishing, 2013: 25.
[18] 王蕾,景安磊,佟威.PISA中国独立研究实践对构建中国特色教育质量评价体系的启示——基于PISA2009中国独立研究[J].教育研究,2017(1):114–123.
[19] 吴桂翎,辛涛,张文静.学校教育资源对学生数学素养预测效应的跨文化比较[J].心理科学,2012(2):352–357.
[20] 黄正正,郭亚歌.学校因素对学生数学素养成绩影响的跨文化比较:基于PISA2012多水平分析的结果[J].中国考试,2014(10):47–56
[21] 喻平.数学教学心理学[M].北京:北京师范大学出版社,2018:289.
[22] 张夏雨.基于关系—表征复杂性模型的有背景问题难度研究[J].数学教育学报,2010,19(3):46–49.
[23] 辛自强.关系—表征复杂性模型的检验[J].心理学报,2003(4):504–513.
[24] 罗增儒.关于情景导入的案例与认识[J].数学通报,2009,48(4):1–6,9.
[25] 杨玉东,张波.教师运用数学问题情境教学的潜在观念和理论倾向[J].上海教育科研,2014(11):54–56.
[26] 王鼎.PISA数学测评核心能力运用启示[J].外国中小学教育,2014(2):11–16.
Investigating Fourth Graders’ Performance in Solving Situation-Based Mathematical Problems in Hunan Province
DENG Hai-ying1, WEI Ya-nan2, YAN Qing3
(1. School of Mathematics and Computational Science, Hunan First Normal University, Hunan Changsha 410205, China;2. School of Mathematical Sciences, Nanjing Normal University, Jiangsu Nanjing 210023, China;3. Institute of Curriculum and Teaching, Nanjing Normal University, Jiangsu Nanjing 210097, China)
Solving situation-based mathematical problems refers to those leaners need to formulate a mathematical problem from a situation and analyze and solve it. The ability to solve such situation-based problems can be divided into three levels: understanding, knowledge transfer, and innovation. The results of this study show that: (1) the fourth-grade students in a Hunan elementary school are at a low level in solving situation-based mathematical problems; (2) there are no gender differences in solving situation-based mathematical problems; (3) there are significant differences between urban and rural students in solving such mathematical problems; and (4) students’ achievement in mathematics is closely related to their ability at solving situation-based problems in general, mainly due to the component of knowledge transfer.
fourth graders; situation-based mathematical problems; problem solving
G622
A
1004–9894(2020)04–0052–06
邓海英,魏亚楠,严卿.小学四年级学生数学情境问题解决能力调查研究——以湖南省为例[J].数学教育学报,2020,29(4):52-57.
2020–02–07
国家社会科学基金教育学一般项目——中学生学科核心素养的评价研究(BHA170150);湖南第一师范学院校级教改课题——立德树人视域下师范生小学数学教育理论水平与教学实践能力双重提升的教学改革研究(XYS19J36)
邓海英(1982—),女,湖南邵阳人,讲师,硕士,主要从事课程与教学论和小学数学教育研究.
[责任编校:周学智、陈汉君]
