高中生直观想象素养的测量与评价研究
2020-08-29郑雪静陈清华王长平林京榕
郑雪静陈清华王长平林京榕
高中生直观想象素养的测量与评价研究
郑雪静1,2,陈清华1,王长平1,林京榕3
(1.福建师范大学 数学与信息学院,福建 福州 350117;2.泉州师范学院 数学与计算机科学学院,福建 泉州 362000;3.福建省尤溪第一中学,福建 尤溪 365100)
直观想象素养是新一轮普通高中数学课程改革凝练的6个数学学科核心素养之一.基于数学学科核心素养的评价是课程改革的突破口.通过情境的复杂程度和图形的呈现形式,构建一个更加精细、更具可操作性的5层次直观想象素养水平评价框架,利用编制的直观想象素养测评试卷,对福建省2 111名高二学生进行测试.结果表明:(1)测评试题难度从类型一到类型二再到类型三呈递增趋势,情境的复杂程度与图形的呈现形式对学生直观想象素养水平要求的高低存在差异;(2)学生直观想象素养水平一般.总体而言,只有三成的学生达到层次4的水平;(3)男生与女生直观想象素养水平存在显著差异;(4)市区、县城、乡镇不同地域学生直观想象素养水平不均衡.
高中生;直观想象素养;评价框架;测评
1 问题提出
评价是课程改革的突破口,随着新一轮普通高中数学课程改革的推进,基于数学核心素养的评价研究迫在眉睫.直观想象素养是高中数学课程改革凝练的6个数学学科核心素养之一.通过文献梳理发现,当前学术界对直观想象素养的研究更多是关注直观想象素养的内涵与结构、直观想象素养的培养、直观想象素养的试题考查、直观想象素养的评价等方面的研究[1-11].其中,关于直观想象素养的评价研究有喻平构建了关于数学核心素养的三级水平评价框架:知识理解、知识迁移和知识创新;董林伟等对初中数学学科核心素养的水平进行了三级划分,并将三级指标从高到低分为、、、四个水平;徐德同等基于2016年江苏省八年级学生学业质量监测,对江苏省八年级学生的直观想象发展水平的基本状况进行了研究;张和平构建了小学生几何直观能力测评模型:=0.3+0.3+0.4,其中,代表“小学生几何直观能力”,符号、、分别代表形成图形的认识、利用图形描述问题、利用图形分析问题3个指标;殷殿宇从内容、结构和过程3个维度构建了直观想象素养的复制、联系、反思3水平测评框架;沈晓凯基于董林伟的研究,构建了高中生直观想象素养4个水平的评价框架;翁艳萍以“向量与几何”的知识团为例,对高中生直观想象素养水平进行了测评研究.综上可见,对学生直观想象素养的评价研究,主要以小学、初中学生为主,且测试内容也相对片面.
因此,试图以高中的函数、几何与代数、概率与统计为内容主线,从情境的复杂程度和图形的呈现形式,构建一个更加精细、更具可操作性的五层次直观想象素养水平评价框架,利用编制的直观想象素养测评试卷,通过大样本对高中生直观想象素养水平现状进行研究,以期为高中生直观想象素养的评价提供借鉴.
2理论基础
2.1 直观想象素养的内涵与价值
《普通高中数学课程标准(2017年版)》(以下简称《课标(2017年版)》)从内涵、价值、表现对直观想象素养进行描述[12]:“直观想象是指借助几何直观和空间想象感知事物的形态与变化,利用空间形式特别是图形,理解和解决数学问题的素养.主要包括:借助空间形式认识事物的位置关系、形态变化与运动规律;利用图形描述、分析数学问题;建立数与形的联系,构建数学问题的直观模型,探索解决问题的思路.”可见,直观想象虽是一个新的名称,却不生疏,它是《普通高中数学课程标准(实验)》中“空间想象”和《义务教育数学课程标准(2011年版)》中所提及的“空间观念”“几何直观”的融合与凝练,是从几何学的视角——“几何直观”“空间想象”“空间形式”“图形”等进行的描述,凸显了直观想象的几何特征.
《课标(2017年版)》还指出:“直观想象是发现和提出问题、分析和解决问题的重要手段,是探索和形成论证思路、进行数学推理、构建抽象结构的思维基础.通过高中数学课程的学习,学生能提升数形结合的能力,发展几何直观和空间想象能力;增强运用几何直观和空间想象思考问题的意识;形成数学直观,在具体的情境中感悟事物的本质.”可见,直观想象不仅是着眼于学生“四能”的培养,还着力于学生数形结合、几何直观、空间想象能力的发展,而且更为宏观地期望通过直观想象素养的发展,学生借助直观想象思考问题、感悟事物本质的能力得以提升;直观想象能够成为学生论证思路、推理、抽象的思维基础.这些正是直观想象素养的数学学科价值和育人价值.
直观想象素养与数学抽象、逻辑推理、数学建模、数学运算、数据分析等另外5个数学学科核心素养密不可分.直观想象是数学抽象、数学建模的基础,也是发现、得到数学结论的思想方法.在复杂的情境中发现、提出和解决问题时,往往需要通过直观想象对问题进行分析,探索问题的本质,再通过数学抽象或数学建模将其数学化.数学中的抽象并非无根之本、无源之水,其“根和源”是具体的、形象的.在进行逻辑推理或数学运算时,通常需要运用直观想象来理清逻辑推理或数学运算的思路,通过思考、想象、猜想一些可能的结论,探寻逻辑推理或数学运算的方向和路径,将问题简捷化、形象化.很多数学家认为,结果常常是“看”出来的,思路也常常是“看”出来的.在进行大数据分析时,通常需要借助直观想象将数据图表化,再利用图表和相关统计方法对数据进行分析和处理.可见,6个数学学科核心素养既相互独立,又相互交融,是一个有机整体.
2.2 直观想象素养的评价理念
《课标(2017年版)》从情境与问题、知识与技能、思维与表达、交流与反思4个维度将直观想象素养划分为3个水平:水平一是高中毕业应当达到的要求,也是高中毕业的数学学业水平考试的命题依据;水平二是高考的要求,也是数学高考的命题依据;水平三是基于必修、选择性必修和选修课程的某些内容对数学核心素养的达成提出的要求,可以作为大学自主招生的参考.《课标(2017年版)》从宏观的角度对直观想象素养进行水平划分,但对于开展直观想象素养的测量与评价,其精细度不够,操作性不强.
《课标(2017年版)》强调:对直观想象素养的评价,应该以课程目标、学业质量标准为依据,注意阶段性、连续性与整体性,结合教学内容,通过创设合适的情境,围绕直观想象素养4个方面的主要表现进行评价:建立形与数的联系、利用几何图形描述问题、借助几何直观理解问题、运用空间想象认识事物.可以从以下4个递进层次对直观想象素养的评价作进一步理解[13]:第一层次:能够建立数与形联系;第二层次:图形描述.即能够借助几何图形的形象关系去描述一个相对复杂、抽象的问题,把研究的问题图形化;第三层次:几何直观(图形)理解.即能够对空间形式和数量关系进行直接感知、整体把握,从而把复杂的数学问题简捷化、形象化,促进数学的思考与想象;第四层次:能够运用空间想象认识事物.即能够根据物体特征抽象出几何图形,或根据几何图形想象出所描述的物体及物体的方位和位置关系,描述图形的运动和变化.
2.3 Van Hiele理论
20世纪50年代荷兰学者范希尔夫妇(Pierre Van Hiele & Dina Van Hiele)在长期的实践研究基础上提出Van Hiele理论,他们将几何思维划分为5个水平[14].水平1——视觉(visuality):辨认和操作几何图形;水平2——分析(analysis):建立图形特性,描述几何对象;水平3——非形式化的演绎(informal deduction):建立图形与图形性质的关系,进行非形式化推论;水平4——形式的演绎(formal deduction):单一公理系统下建立定理,进行逻辑推理证明;水平5——严密性(rigor):在不同公理系统下严谨建立定理.到了20世纪80年代,Van Hiele又将5个思维水平合并为3个[15]:直观水平(visual level)、描述水平(descriptive level)、理论水平(theoretical level).三水平分类法中的3个层次虽然更为清晰,但目前用得更多的是五水平分类法.Van Hiele建立的几何思维水平体系,是关于学生几何概念发展与学习研究中最有影响的理论之一[16-17],对构建直观想象素养的评价框架具有一定的借鉴意义.
3 直观想象素养的评价框架
情境是知识转化为素养的重要途径,没有情境的知识就只剩下符号,知识的产生、应用及背后蕴含的思想方法就无从谈起.没有数学内容,数学能力也不能被激活和发展,数学素养就没有根基,也就没有考查的基础.因此,对学生直观想象素养的评价应注重借助情境和数学内容.根据情境的复杂程度以及图形呈现的形式,将直观想象素养的评价分为3种类型,结合《课标(2017年版)》中直观想象素养三水平划分及评价理念,借鉴Van Hiele理论,构建了直观想象素养的评价框架(表1).

表1 直观想象素养的评价框架
4 测评过程
4.1 测评试卷编制
测评试卷的编制,以《课标(2017年版)》中关于学业水平考试和高考命题的建议为指导,以函数、几何与代数、概率与统计为内容主线,以学习数学的4个层次(知识内容是基础、思想方法是根本、能力意识是目的、核心素养是本质)和直观想象素养的4个方面表现为依据,以表1评价框架为标准,注重考查学生直观想象素养的能力和意识.主要包括数形结合、几何直观、空间想象等能力;能够主动运用直观想象去思考问题;在感悟事物上能借助数学直观,依托情境去感悟事物的本质等意识.当然,直观想象素养与其它5个数学学科核心素养紧密相联,这里侧重评价的是学生的直观想象素养.
测评试卷是经过十多名研究生多轮讨论,同时综合一线教师和多位专家的意见编制,有课标中的案例原题或改编的题,有自编的题,最后设置10道与直观想象素养紧密相关的试题,其中两道客观题除了要求选择和填空外,还要求说明选择的理由和填空的具体解答过程,测试时间为120分钟.考虑到测试内容的知识水平,选择的测试时间段是高二下半学期.
4.2 测评试题水平分析
以表1的评价框架为依据,将测评试题分为3种类型(类型一有4道题、类型二和类型三各3道题),下面以一道试题为例,对直观想象素养的水平评价进行分析(表2).
4.3 前测及分析
为保证测试更加科学有效,对测试卷进行前测研究.以某一级达标高中高二年级两个班级的学生为前测对象,班级学生的总体水平中等以上,回收有效问卷88份,其中男生52人,女生36人.测试卷的内部一致性信度为0.851,具有较好的信度[18];试卷区分度为0.73,具有较好的区分度;试卷难度系数为0.30,总体难度较大.测试结果统计分析发现,第10题的难度系数为0.09,这出乎预料,该题是《课标(2017年版)》的案例31,从学生答题分析,困难主要在于对图形的推理论证,也可能与该题处于试卷最后一道题有一定关系.第9题难度系数为0.05,试题难度最大.第6题属于数据统计分析题,学生反馈该题比较常规.
在前测基础上,对测试题进行适当调整,把原第10题调整至第5题;将原第9题设置为两小题,以分解试题的难度;删除第6题,用一道几何概型题替换.最终形成一份10道测评高二学生直观想象素养水平的试卷(第1、2、3、5题属于类型一,第4、6、7题属于类型二,第8、9、10题属于类型三),并制定详细的评分标准,开展正式测评.
4.4 正式测试及分析
采用分类和整群相结合的随机抽样方法,以福州、莆田、泉州、厦门、三明等市区、县城、乡镇中学的高二学生为正式测评对象,样本覆盖面比较广,具有一定的代表性,共回收有效问卷2 111份,其中男生1 178份,女生933份.具体地区样本量及所占比例见图1.
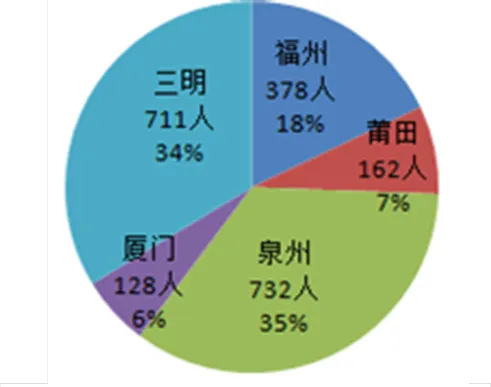
图1 样本量及地区分布
对回收的2 111份有效测试卷,由多名中学一线数学教师根据评分标准进行初评,并由作者逐份复评,当初评与复评分数不一致时,通过讨论协商确定分数.对于第4题和第6题,常见有数形结合(记为“J”)和代数方法(记为“D”)两种解法,为尽可能地不仅关注学生解答的正确程度,也力求通过解题方法和策略进行辅助诊断,采用TIMSS双重计分制进行成绩录入.录入前对试卷进行6位数编码:地区、学校、性别(男生编码1,女生编码2)、三位数编号,如福州一中女生第18份试卷编码为AY2018.采用SPSS22统计软件进行数据分析.

表2 直观想象素养水平评价试题分析
(1)试卷信度分析.
采用信度系数的内部一致性信度,对2 111份样本的10道测试题(第1题和第6题以主观题形式参与分析)得分进行信度分析,结果显示:测试卷的信度系数为0.808,具有较好的信度,说明这份测试卷测试结果具有较高的可靠性(见表3).

表3 信度分析
(2)试卷难度与区分度分析.
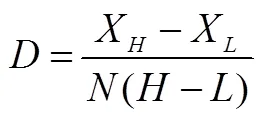
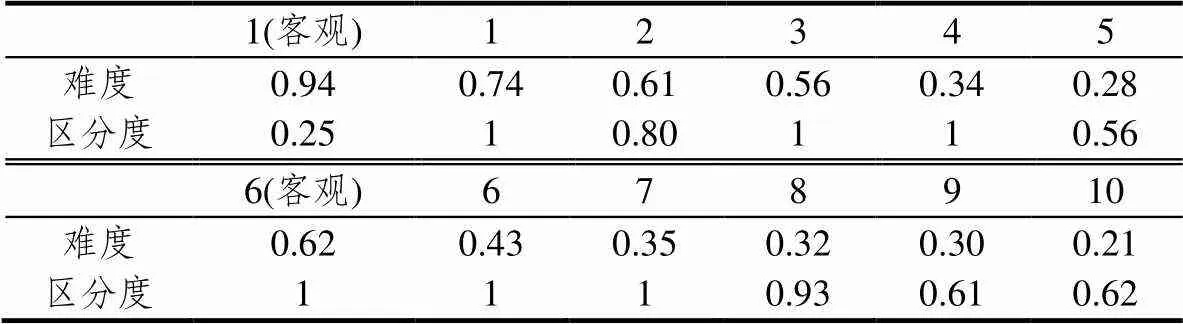
表4 试题的难度和区分度
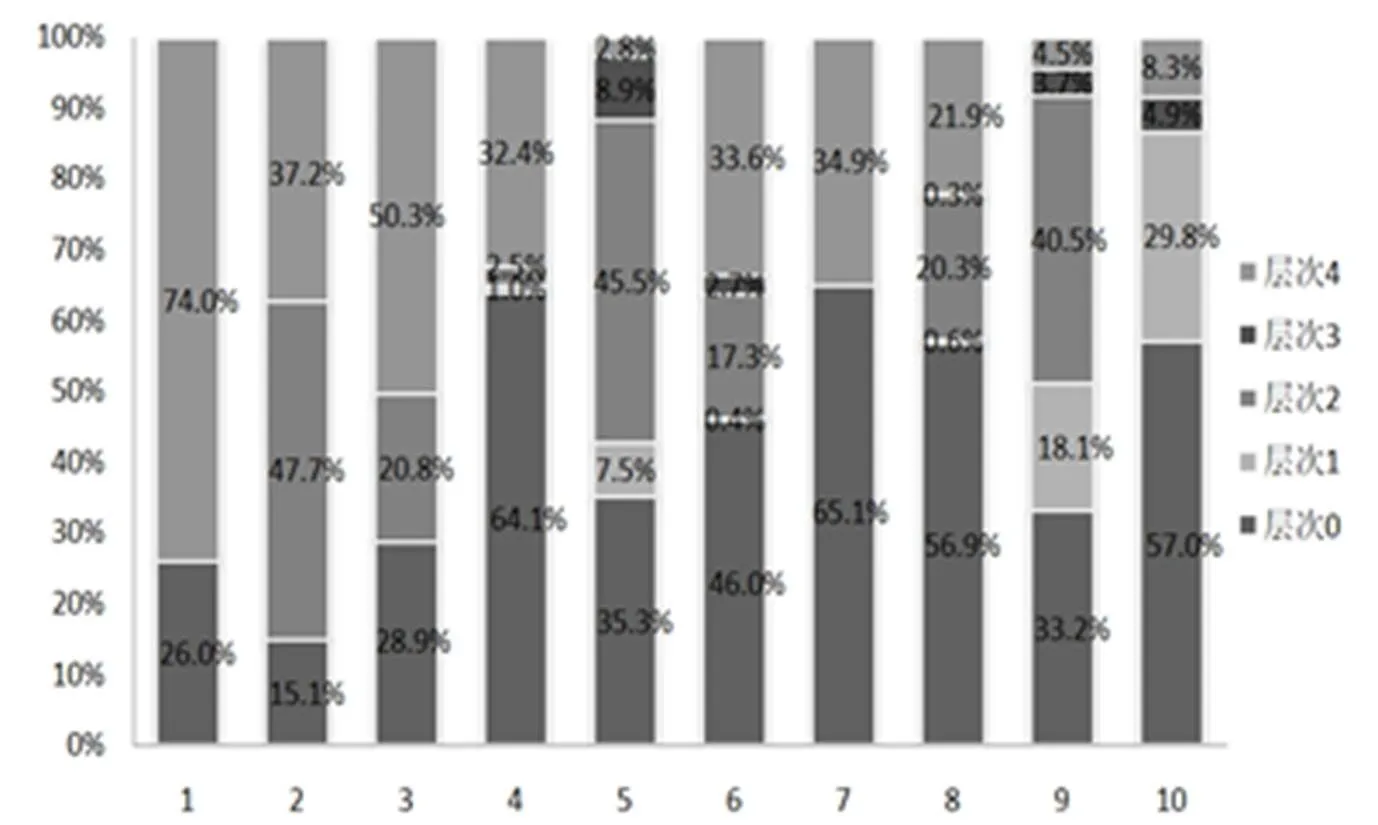
图2 高中生直观想象素养水平的层次分布
表4显示,类型三的试题难度最大,第8、9、10题的难度分别为0.32、0.30、0.21;类型二试题的难度比类型三略低,第4、6、7题的难度分别为0.34、0.43、0.35,第6题作为客观性试题难度为0.62,属于比较容易的试题,相比作为主观性试题难度降低很多;类型一试题难度属于中等偏易,第1、2、3题的难度分别为0.74、0.61、0.56,但第5题的难度为0.28,与前侧放在最后一题时难度为0.09相比,降低了很多,但仍较难.整个试卷难度采用各题难度与分值权重的乘积的总和进行计算,试卷难度系数为0.39,具有一定难度.对于区分度,除了第1题作为选择题,区分度仅为0.25,区分度一般外,其它试题的区分度都非常好.整个试卷区分度采用各题区分度与分值权重的乘积的总和进行计算,试卷区分度为0.85,具有很好的区分度.
(3)高二学生直观想象素养水平分析.
对每道测试题得分的情况进行统计,分析高中生直观想象素养水平的层次分布情况.
图2显示各题学生的直观想象素养水平的层次百分比,其中,属于类型一的第1题,学生达到层次4的比重最大,有74.0%,最少的是第5题,层次4的比重仅为2.8%;将类型一的4道试题进行层次求和平均,得出学生直观想象素养水平处于层次0、1、2、3、4的比例分别为26.3%、1.9%、28.5%、2.2%、41.1%,有四成多的学生水平达到最高层次;属于类型二的3道试题,学生达到层次4的百分比差不多,在32%至35%之间,但第4题和第7题处于层次0的分别有64.1%、65.1%,将类型二的3道试题进行层次求和平均,得出学生直观想象素养水平处于层次0、1、2、3、4的比例分别为58.4%、0.5%、6.6%、0.9%、33.6%;属于类型三的第9题,学生达到层次4的百分比最小,仅4.5%,第8题达到层次4的学生有21.9%,将类型三的3道试题进行层次求和平均,得出学生直观想象素养水平处于层次0、1、2、3、4的比例分别为49.0%、16.2%、20.3%、2.9%、11.6%.将10道试题进行层次求和平均,得出学生直观想象素养水平处于层次0、1、2、3、4的比例分别为42.8%、5.7%、19.5%、2.0%、30.0%,总体而言,只有三成学生达到层次4的水平.
(4)高二男、女生直观想象素养水平差异显著性检验.
对男、女生直观想象素养水平测试成绩进行独立样本检验.结果如表5、表6所示.

表5 基本描述性统计量
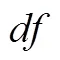

表6 独立样本t检验结果
(5)市区、县城、乡镇的高二学生直观想象素养水平差异显著性检验.
将测评对象所在学校分成市区、县城、乡镇3种类型,采用单因素方差分析,对这3类学校学生的直观想象素养水平进行差异显著性检验.具体见表7~表10.
表8是莱文方差齐性检验结果,显著性概率=0.00<0.05,表明市区、县城、乡镇3类学校的方差在0.05的显著性水平上差异显著,即3类学校方差是不齐的.表9显示,3类学校学生直观想象素养水平的平均成绩之间存在显著的差异(=126.177,=0.00<0.01).用检验进行各类学校均值配对比较,事后分析的多重比较结果显示(表10):市区与县城、市区与乡镇、县城与乡镇之间的平均成绩均存在显著性差异.从平均值来看,市区为46.54,县城为36.42,乡镇为25.53,市区学生直观想象素养的平均水平比县城高,县城学生直观想象素养的平均水平比乡镇高.
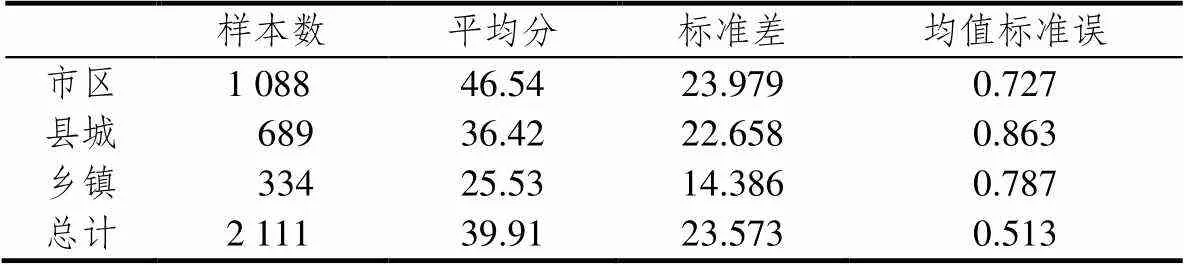
表7 描述统计量

表8 方差齐性检验
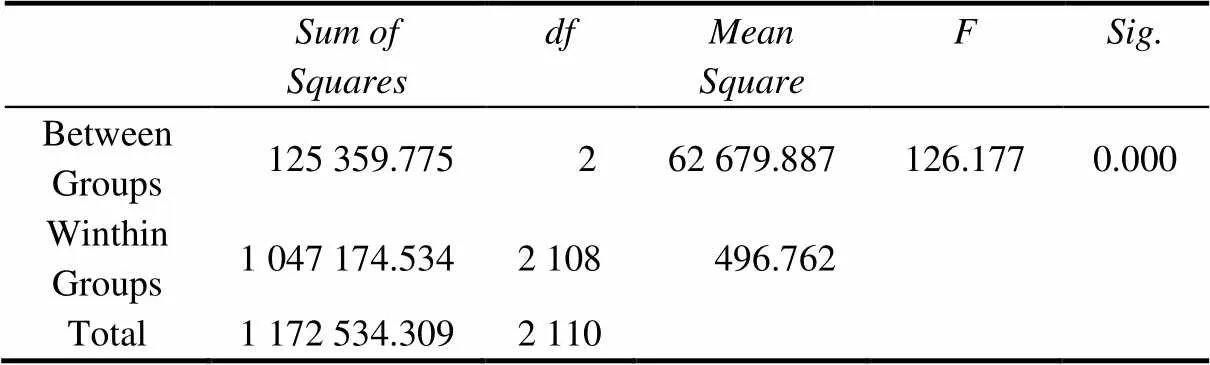
表9 方差分析表

表10 均值多重比较
5 结论
(1)测评试题难度随着试题类型的不同而不同,从类型一到类型二再到类型三,试题的难度呈递增趋势.情境的复杂程度与图形的呈现形式对学生直观想象素养水平要求的高低存在差异.
(2)福建省高二学生直观想象素养水平一般.对于类型一、类型二、类型三的试题,学生达到层次4水平的比例呈现明显的递减趋势.总体上,只有三成的学生达到层次4的水平.
(3)高二男生与女生直观想象素养水平存在显著差异,总体上,男生直观想象素养的平均水平比女生高.
(4)市区、县城、乡镇不同地域高二学生直观想象素养水平不均衡.总体上,市区学生直观想象素养的平均水平比县城高,县城学生直观想象素养的平均水平比乡镇高.
6 反思与讨论
6.1 控制测评试题的难度
根据数据分析,类型一、类型二、类型三测评试题的难度呈递增趋势.可见,情境的复杂程度、图形的呈现形式对学生直观想象素养水平的测评存在较大影响.通过情境复杂性和图形的呈现形式来控制测评试题的难易程度将是一种有效途径.
6.2 协同直观想象与逻辑推理的发展
测试题第1题作为选择题,有94%的人选对,但要求学生说明选择的理由时,只有74%的学生解释合理.测试题第5题,有56.9%的学生能够画出1~3种图形,有7.6%的学生能够把所有可能的图形完整画出.但要求学生对结论进行推理论证时,仅有2.8%的学生能够严格推理论证,还有86.9%的学生完全不懂得如何推理论证.
直觉与逻辑的完美结合是数学发展与学生思维发展的根本之道[19],应该追寻直觉背后的逻辑与引领逻辑的直觉.在培养学生直观想象素养的同时,也要注重学生逻辑推理素养的协同发展,以促进学生思维的发展.
6.3 加强学生直观想象意识的培养
测试题第4题,对于直观想象素养意识较强的学生,很快就能找到证明思路:将问题转化为寻找椭圆上到原点最大距离的点和最小距离的点.在直角坐标系中将椭圆画出,即可直观看出距离的最大值与最小值的点分别在椭圆的右端点和左端点.当然,该题也可以用代数方法或极坐标方程求解,但相比图形直观的方法,其求解过程要复杂得多.2 111个样本中,只有20.9%的学生用数形结合的方法,有15.6%的学生用代数方法.可见,具有较强直观想象意识的学生,在解决问题过程中可以起到事半功倍的效果,应该加强对学生直观想象意识的培养.
6.4 培养学生更高层次的直观想象素养水平
6.5 均衡地域之间学生直观想象素养的发展
高中学生的直观想象素养水平存在地域间的显著差异.文[21]的研究结果也表明高中学生的数学抽象素养水平存在地域间的显著差异.“素养”理念下的数学教育如何进一步缩短地域差异,推进教育公平?这是整个教育部门需要认真思考的问题[22-32].
6.6 关注直观想象素养与其它数学核心素养之间的影响
研究侧重的是直观想象素养,但一道测试题并不能完全只涉及直观想象素养的考查,数学抽象、逻辑推理、数学运算等其它数学核心素养是否会影响直观想象素养水平的考查,需要进一步的关注.
[1] 吴立宝,刘哲雨,康玥媛.直观想象素养的内涵与结构探究[J].现代基础教育研究,2018,31(3):109-113.
[2] 高文龙.高中数学直观想象素养的培养研究[J].数学学习与研究,2018(22):130.
[3] 胡云飞.基于提升直观想象素养的立体几何法则课的设计与反思——以《直线与平面垂直》为例[J].数学通报,2016,55(12):24-26,31.
[4] 戴有刚.直观想象在2018年高考理科数学试卷中的体现[J].现代中小学教育,2018,34(12):55-58.
[5] 喻平.数学核心素养评价的一个框架[J].数学教育学报,2017,26(2):19-23,59.
[6] 董林伟,喻平.基于学业水平质量监测的初中生数学核心素养发展状况调查[J].数学教育学报,2017,26(1):7-13.
[7] 徐德同,钱云祥.基于质量监测的初中学生直观想象发展状况的调查研究[J].数学教育学报,2017,26(1):22-24.
[8] 张和平,裴昌根,宋乃庆.小学生几何直观能力测评模型的构建探究[J].数学教育学报,2017,26(5):49-53.
[9] 殷殿宇.高中生数学直观想象水平调查研究[D].苏州:苏州大学,2017:18-20.
[10] 沈晓凯.直观想象素养现状测评研究[D].武汉:华中师范大学,2018:18-20.
[11] 翁艳萍.高中生数学直观想象素养测评研究[D].福州:福建师范大学,2017:1-64.
[12] 中华人民共和国教育部.普通高中数学课程标准(2017年版)[M].北京:人民教育出版社,2018:6.
[13] 史宁中,王尚志.普通高中数学课程标准解读(2017年版)[M].北京:高等教育出版社,2018:114-126.
[14] 鲍建生,周超.数学学习的心理基础与过程[M].上海:上海教育出版社,2009:4-5.
[15] VAN HIELE P M. Structure and insight: A theory of mathematics education [M]. Orlando, FL: Academic Press, 1986: 80-86.
[16] BATTISTA M T. The development of geometric and spatial thinking [M] // LESTER F K. Second handbook of research on mathematics teaching and learning. Charlotte, NC: Information Age, 2007: 843-908.
[17] CLEMENTS D H, BATTISTA M T. Geometry and spatial reasoning [M] // GROUWS D A. Handbook of research on mathematics teaching and learning. New York, NY: National Council of Teachers of Mathematics/Macmillan Publishing Co, 1992: 420-464.
[18] 吴明隆.问卷统计分析实务——SPSS操作与应用[M].重庆:重庆大学出版社,2010:237.
[19] 李昌官.追寻直觉背后的逻辑与引领逻辑的直觉[J].数学教育学报,2018,27(4):76-81.
[20] 史宁中.漫谈数学的基本思想[J].中国大学教学,2011(7):9-11.
[21] 郑雪静,陈清华,王长平.基于测试的高中生数学抽象素养水平现状研究[J].数学教育学报,2017,26(6):26-32.
[22] 王光明,李爽.初中生数学学习非智力因素调查问卷的编制[J].数学教育学报,2020,29(1):29-39.
[23] 何勇刚,张立昌.基于结构方程模型的学习策略影响因素探究——以初中生学习“统计与概率”为例[J].数学教育学报,2020,29(1):40-47.
[24] 柯跃海,陈清华.高考数学命题质量评价的基础与方法[J].数学教育学报,2020,29(1):48-51.
[25] 傅海伦,张丽,王彩芬.基于Fuzzy-AHP质疑式数学核心素养评价指标体系的研究[J].数学教育学报,2020,29(1):52-57.
[26] 任子朝,佟威,赵轩.高考试题难度预估的校准与改进研究[J].数学教育学报,2019,28(6):1-4.
[27] 陈婷,孙彬博,张彩云.百年高中数学课程能力目标发展的回眸与反思——基于课程标准(教学大纲)的文本分析[J].数学教育学报,2019,28(6):5-9.
[28] 严必友,宁连华,赵静亚.高中学生数学书写状况的调查研究[J].数学教育学报,2019,28(6):10-15.
[29] 黄翔,童莉,李明振,等.从“四基”“四能”到“三会”——一条培养学生数学核心素养的主线[J].数学教育学报,2019,28(5):37-40.
[30] 李红云,朱文芳,伍春兰.学生统计思维发展水平划分探究[J].数学教育学报,2019,28(5):41-46.
[31] 邓清,夏小刚.数学思维视域下“教表达”的再认识与思考[J].数学教育学报,2019,28(5):47-50.
[32] 宁锐,李昌勇,罗宗绪.数学学科核心素养的结构及其教学意义[J].数学教育学报,2019,28(2):24-29.
Measuring and Evaluating Senior High School Students’ Intuitive Imagination Literacy
ZHENG Xue-jing1, 2, CHEN Qing-hua1, WANG Chang-ping1, LIN Jing-rong3
(1. College of Mathematics and Informatics, Fujian Normal University, Fujian Fuzhou 350117, China; 2. College of Mathematics and Computer Science, Quanzhou Normal University, Fujian Quanzhou 362000, China;3. Fujian Youxi No.1 High School, Fujian Youxi 365100, China)
Intuitive imagination literacy is one of the six core literacies of mathematics in the new mathematics curriculum reform for high school. Evaluation based on the mathematics core literacies is a breakthrough in curriculum reform. This study constructed a five-level framework to evaluate intuitive imagination literacy based on the complexity of the situation and image presentation. A test for measuring students’ intuitive imagination literacy was developed based on the five-level framework and was then administered to 2,111 junior high school students in Fujian province. The results showed that: (1) The difficulty of the test increases from Type 1, Type 2, and to Type 3, and there was a significant difference between the complexity of the situation and visual representations on the requirements of students’ intuitive imagination; (2) only 30% of students reached Level 4; (3) there were significant differences between female and male students’ intuitive imagination literacy; and (4) there were significant differences in intuitive imagination literacy among the students who came from urban cities, rural town centers, and countryside.
high school students; intuitive imagination literacy; evaluation framework; measurement
G633.6
A
1004–9894(2020)04–0007–06
郑雪静,陈清华,王长平,等.高中生直观想象素养的测量与评价研究[J].数学教育学报,2020,29(4):7-12.
2020–03–06
2016年全国教育科学规划课题——高中生数学核心素养培养的策略及评价研究(DHA160364)
郑雪静(1978—),女,福建泉州人,副教授,博士,主要从事数学教育、考试命题与评价研究.
[责任编校:陈隽、陈汉君]
