基于独立分量分析的物联网多设备通信干扰抑制方法
2020-08-28郑潇
郑 潇
(福建商学院 信息工程学院,福建 福州 350506)
物联网(Internet of Things,简称IOT)是采用多个信息传感器、全球定位系统和激光扫描器等多种设备和技术,完成对人、机、物的智能化感知、识别和管理[1].物联网多设备在通信过程中会存在跳频通信(Frequency Hopping,FH),跳频通信会根据射频频率的变化产生伪随机跳变,能够减少跳频信号被查验的概率,加强通信安全性,因此跳频信号在物联网多设备通信中被广泛应用[2].但是,随着物联网多设备通信干扰信号的增多,干扰方式逐渐多元化,其中以梳状阻塞干扰为主要代表,所以物联网多设备跳频通信的抗干扰能力逐渐降低,已经无法满足实际需求.梳状阻塞干扰信号的干扰频率较高,主要原因在于梳状阻塞干扰能够将有限功率聚集在跳频信号的各个频点,严重干扰了跳频信号的传输[3-5].因此,提升物联网多设备通信抗梳状阻塞干扰抑制能力是目前对物联网多设备通信干扰抑制方法研究的重要方向[6].
独立分量分析(Independent Component Analysis,ICA)是在某个衡量独立性的标准下,采用优化算法将一组混合信号分解成多个独立成分.独立分量分析也是一种盲源分离技术,将其应用至物联网多设备通信干扰抑制中,能够实现跳频信号和梳状阻塞干扰信号的分离,实现物联网多设备通信干扰抑制.
1 物联网多设备通信干扰抑制方法
1.1 独立变量分析的混合模型
独立变量分析混合-解混模型如图1所示.
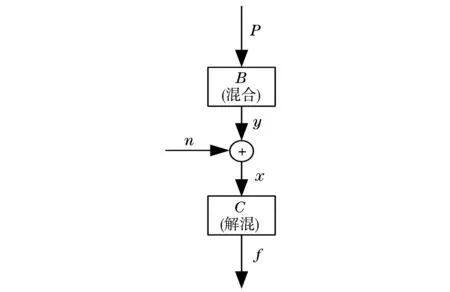
图1 混合-解混模型图
其中,n维的信号源P经过混合矩阵Bm×n转换为m维混合信号y;n维信号x,由y通过加性高斯白噪声信道后获得;n维分离信号f,由x通过解混矩阵Cn×m获得.
独立分量分析问题的混合模型用(1)式表示:
X=BP+k,
(1)
式中,由n个信号源组成的独立向量P=[p1,p2,…,pn]T;n维信号是x=[x1,x2,…,xn]T,代表每个物联网传感器的输出信号;混合矩阵是m×n维矩阵,B=[b1,b2,…,bn]T.n维加性高斯白噪声是k=[k1,k2,…,kn]T.
通过观测信号的高阶统计量进行信号分离是独立分量分析算法的基本理念[7],高斯白噪声对该算法没有影响.暂不考虑噪声的影响,将(1)式简化成(2)式:
y=BP,
(2)
式中,n个信号源经过混合后获得y=[y1,y2,…,ym]T.
独立分量分析问题的解混模型由(3)式表示:
f=Cy=CBP=QP,
(3)
式中,全局矩阵用Q表示.求解解混矩阵C是独立分量分析问题的基本思想,当C=Jn(Jn是n×n阶单位矩阵),则f=P,能够实现分离源信号的目的.在实际应用中,混合信号分离成功的条件是:
(1)全局矩阵Q的各行各列中只有一个元素接近等于1;
(2)其余元素接近等于0.
当能够通过f估计出P和B时,则以没有一切关于P和B的先验知识条件为前提,因此独立分析问题一定能出现很多组解.应做出如下的假设,确保解的唯一性.
(1)源信号pn均值都是0,并在任意时刻都互相独立.信号能够分离的重要前提是源信号间的独立性,该假设在实际情况下非常容易满足,但是在某种特定情况下却难以实现[8];
(2)当源信号中的高斯信号数量是1个或小于1个时,对线性混合后的两个高斯信号实行分离,由于混合后的信号也是高斯信号,其高阶统计量是0,分离后的信号满足统计独立性[9],但是分离结果和源信号不一致,致使分离失败;
(3)当m=n时,B是满秩的可逆矩阵.假如m>n,B是列满秩矩阵,可采用主变量分析法(PCA)实行降维处理,除去冗余信息.
独立分量分析由独立分量分析的混合模型、解混模型和假设条件三者组成.换言之,独立分量分析问题是寻得一个解混矩阵C,使分离后的信号相互独立,尽量靠近源信号pn,使分离效果达到最佳[10].
1.2 独立分量分析抗干扰抑制
基于独立分量分析的物联网多设备跳频通信抗干扰抑制方法原理如图2所示.

图2 通信干扰抑制方法原理图
通过信道编码、中频调制及跳频后获得物联网多设备通信系统的跳频信号p1(t),其序列为J(n).物联网多设备通信系统的干扰信号通过梳状滤波器和功率放大器转变为梳状阻塞干扰信号p2(t).在物联网多设备通信系统的接收端设置两根天线作为独立分量分析分离的基础,则接收信号用(4)式表示:
y(t)=Up(t)+n(t) ,
(4)
式中,两根天线接收信号分别用y1(t)、y2(t)表示;源信号、噪声信号分别用p1(t)、p2(t)表示,噪声信号分别用n1(t)、n2(t)表示.依据上小节分析的独立分量分析问题的混合模型,通过独立分量分析(盲源分离)求出分离矩阵D.
在源信号独立的条件下,P.Comon提出,要想使混合信号完全分离,只要让输出信号互相独立即可实现[11].独立成分分析(ICA)的对照函数可通过输出信号的高阶或二阶累计量矩阵群联合对角化程度表示[12].为了完成源信号的全部分离,需要判断怎样利用四阶累计量矩阵群和对角化相结合的方式求解分离矩阵并以四阶累计量为起点.
设定第N个通道观测信号是v,权值矩阵E,则v=(v1v2…vN)T,式(5)表示v的四阶累计量矩阵的第i行第j列(1≤i,j≤N)元素,如式(5)所示:
(5)
式中,向量v中第i、j、k、l4个分量的四阶累计量是cum(vi,vj,vk,vl);v的全部四阶累计量组成的累计量矩阵为Gz(E);权值矩阵E的第k行、第l列元素是ekl.
式(6)表示白化后第N个通道的观测向量v,如下所示:
v=WUP=RP,
(6)
式中,P中每个分量统计独立,v中每个分量之间没有关系[13].因此矩阵R是正交矩阵.假设ri(1≤i≤m)表示R的任意一列,ri=(ri1ri2…rim)T,则矩阵E是:
E=rivN.
(7)
将式(6)、(7)式代入式(5)可得:
cum(pa,pb,pc,pd)],
(8)
由于每个源信号相互独立,当a=b=c=d时,cum(pa,pb,pc,pd)=k4(pa),(8)式可以简化成:
[Gv(E)]ij=mijk4(pk) ,
(9)
即:
Gv(E)=k4(pk)E,
(10)

Gv(E)=DΛ(E)RT,
(11)
式中,特征值对角矩阵是Λ(E).
对角矩阵Λ(E)通过矩阵R对Gv(E)做二次型处理获得,依据整个特性能够求解分离矩阵.
选取一组z个矩阵E=(E1E2…Ez),对任意一个Ez(1≤z≤Z)求Gv(Ez),并求出矩阵R,尽量使每个Gv(Ez)都完成对角化处理.利用每个Λ(Ez)中非对角元素的平方和作为度量指标,完成对每个Λ(Ez)=RTGv(Ez)R的非对角化程度的度量,如下所示:
(12)
因此,获得详细的分离算法为:

(2)随意选择一组矩阵E=(E1E2…Ez),求解一组累计量矩阵Gv(Ez);
(3)矩阵R对各Gv(Ez)联合对角化,使得非对角指标Hm(R)非常小;
(4)估计分离矩阵D,
D=RTW.
(13)
通过独立分量分析,有效分离出了物联网多设备跳频信号和干扰信号[14-15],实现物联网多设备通信的干扰抑制.
2 实验分析
采用MATLAB编写仿真程序对本文方法进行仿真实验.实验对象为某电力公司的物联网多设备通信系统,该通信系统中的跳频信号利用2FSK方法调制,跳频点数是7个,跳速、信息速率和采样频率分别是1 500 hops/s、1 500 b/s和400 kHz,梳状阻塞干扰信号的梳齿共7个,每个跳频频点都对应一个梳齿中心.图3是实验电力公司物联网多设备通信系统的源信号频谱,该信号是一个混合信号,包含跳频信号、梳状阻塞干扰信号.

频率/kHz(a)跳频信号频谱图

频率/kHz(b)梳状阻塞干扰信号频谱图图3 源信号频谱图
源信号噪声幅值如图4所示.

时间/s图4 源信号噪声幅值
从图3、图4中能够看出,跳频信号幅度值远远小于梳状阻塞干扰信号幅度值,且源信号噪声幅值较高,需要对该信号进行去噪处理,以提升物联网多设备通信干扰抑制效果.
选择文献[4]方法、文献[5]方法作为实验对比方法,验证这三种方法对实验通信系统中的混合信号分离效果,得到的源信号和分离信号的相似系数用表1描述.相似系数取值越靠近1,说明信号源和分离信号的相关性越好,则干扰信号的分离效果越好,反之越靠近0,干扰分离效果越不好.
分析表1可知,采用本文方法后,4种混合信号分离的信号源和分离信号的相似系数非常靠近1,而其它两种方法的相似系数远小于1,进一步说明本文方法能够有效抑制物联网多设备通信的梳状阻塞干扰.

表1 信号源和分离信号的相似系数
为了进一步验证不同方法的性能,测试应用这3种方法后物联网多设备通信信号的噪声幅值,噪声幅值越低,说明该方法的抑制效果越好,结果如图5所示.
分析图5可知,与文献方法相比,经过本文方法处理后的物联网多设备通信信号的噪声幅值明显下降,说明该方法能够实现物联网多设备通信干扰抑制.

时间/s(a)文献[4]方法

时间/s(b)文献[5]方法

时间/s(c)本文方法图5 信号噪声幅值对比
3 结 论
为提高物联网多设备通信抗干扰能力,提出基于独立分量分析的物联网多设备通信干扰抑制方法.依据独立分量分析的统计独立性,对物联网多设备跳频信号和梳状阻塞干扰信号进行统计独立性分析与分离,完成对物联网多设备通信梳状阻塞干扰的有效抑制,为物联网多设备通信的顺利进行创造了可靠条件.
