例说中学数学中的周期问题

江苏省苏州市吴中区木渎金山高级中学 董晓莉

在现实生活中，存在周而复始、循环往复的现象，这种周而复始的性质我们称之为周期性，具有这样性质的函数叫周期函数。周期性具有简单、和谐、对称等数学美，也蕴含着等价变换和数形结合的重要数学思想方法。因此，我们要十分重视周期问题，充分利用好周期的属性，帮助我们去分析问题和解决问题。下面例说中学数学中的周期问题，期望能够起到抛砖引玉的作用。

一、周期函数的定义、教学及作用

1.周期函数的定义

对于函数f（x），如果存在一个常数T（T=0），使得当自变量x 取定义域内的任意一个值时，都有f（x+T）=f（x），那么函数f（x）就是周期函数，非零常数T 称作这个函数的周期。对于一个周期函数f（x），如果在它所有的周期中存在一个最小的正数，那么这个最小的正数就叫作f（x）的最小正周期。在周期函数的定义中我们要注意两个地方，一是对任意的自变量x，恒等式f（x+T）=f（x）都应该成立；二是并不是所有周期函数都有最小正周期。

2.周期函数的教学

在高中数学教学中，周期的定义是在三角函数这一章中出现的，这主要是因为三角函数是刻画圆周运动的数学模型，“周而复始”的基本特征蕴含在三角函数的性质之中。课本通过探究和观察三角函数的图像，使学生先直观理解，再抽象掌握周期性及周期的定义，然后学会简单的三角函数的周期求法，因此，教材的安排就显得合情合理了。在此基础上，为今后利用周期性去解决一些实际问题创造了必要条件。

3.周期函数的作用

从周期的定义可以看出，周期函数最大的特点就是函数值f（x+T）和函数值f（x）是相等的，所以其最大的作用之一是在求一个函数值遇到困难时，可以转化为求另一个函数值。另一方面，根据周而复始、循环往复的现象，可以利用数形结合的方法去思考问题。也就是说，我们要从周期的代数意义和几何意义两个方面去考虑解决问题。

二、怎样确定函数的周期

1.代换法

例1：当x ∈R 时，函数y=f（x）满足f（x+2）+f（x-2）=f（x），则y=f（x）是周期函数，它的最小正周期是_。

【分析】运用整体思想去代换，得到f（x+T）=f（x）即可。

【解】用x-2 代替式子中的x，则有f（x）+f（x-4）=f（x-2），于是f（x+2）=-f（x-4），再用x+4 替换式子中的x，得到f（x+6）=-f（x），最后用x+6 替换式子中的x，可得f（x+12）=-f（x+6）=f（x），所以此题的答案为12。

2.公式法

∵2010=4×502+2，

3.归纳法

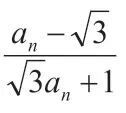
【分析】数列作为一种特殊的函数，它们中间也会存在着一些周期问题，有些数列问题表面上看好像与周期无关，但实际上却隐含着周而复始的数据，在解题中若能揭示其数据规律，便可得到周期数列，使问题得到解决。

三、周期问题的若干实例

周期问题是函数的一个热点问题，它的重要性是不言而喻的，因此经常出现在高考试题中。这就要求学生必须熟练掌握周期问题的有关属性，并且会灵活运用它去解决相关的一些问题，特别要注意它等价变换和数形结合的功能。

例4：设函数f（x）在（-∞，+∞）上满足f（2-x）=f（2+x），f（7-x）=f（7+x），且在闭区间［0，7］上，只有f（1）=f（3）=0。

（1）试判断函数y=f（x）的奇偶性；

（2）试求方程f（x）=0 在闭区间［-2005，2005］上的根的个数，并证明你的结论。

【分析】（1）由题目所给的两个恒等式得到函数是否具备奇偶性；（2）由区间长度联想到该题应与周期相关，所以可先求出函数的周期，再解决问题。

【解】（1）由f（2-x）=f（2+x），f（7-x）=f（7+x）得函数y=f（x）图像的对称轴方程为x=2 和x=7，所以函数y=f（x）不是奇函数。

又f（3）=f（0）=0，而f（7）≠0，故函数y=f（x）即不是奇函数，也不是偶函数；

又f（3）=f（0）=0，f（11）=f（13）=f（-7）=f（-9）=0，故f（x）在[0，10]和[-10，0]上均有两个解，从而可知函数y=f（x）在[0，2005]上有402 个解，在[-2005，0]上有400 个解，所以函数y=f（x）在[-2005，2005]上有802 个解。

【分析】该题解题的关键应是根据函数的周期性画出函数的示意图，再进一步根据数形结合进行求解。

令t=9m2（t ＞0），则（t+1）x2-8tx+15t=0。

【分析】根据函数的周期性平移图像，找出两个函数图像相切或相交的临界交点个数，从而确定参数的取值范围。

又f（x）为奇函数，其图像关于原点对称，周期为4，如下图，作出函数f（x）与g（x）的图像，要使f（x）=g（x）在(0，9]上有8 个实根，只需二者图像有8 个交点即可。

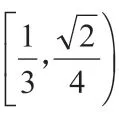
总之，周期是函数的一个重要属性，而学生对它的认知往往是简单肤浅的，这个问题在教学中一定要引起教师的高度重视，要想方设法拓展学生对周期内涵和外延的认知程度，特别是它蕴含的等价变换和数形结合的重要数学思想方法，应该让学生去亲身体验和感受，这对提高学生的数学核心素养大有裨益。