裂隙岩体非线性渗流特性分析

蒙学礼，蒙发强，李涣森，刘振龙，彭鹏程

(1.广西壮族自治区第四地质队，广西 南宁 530033；2.广西第一地质工程公司，广西 南宁 530033)

0 引言

岩体裂隙中的渗流失稳是煤矿及隧道突水、瓦斯突出等动力灾害的表现形式，其原因在于系统的非线性[1]。裂隙岩体渗流已引起普遍关注，并获得了许多有益成果。立方定律是目前应用最广的裂隙渗流模型之一。但受裂隙面粗糙度影响，实际工程中的裂隙岩体渗流与立方定律存在较大偏差。因此，研究者通过考虑粗糙度[2]、接触面积[3]、曲折效应[4]等影响，提出了诸多修正的裂隙渗流模型。同时受粗糙裂隙面影响，还会出现非线性渗流现象[5]。ZHAO通过瞬态法渗流试验，得出裂隙岩体渗流在流速较小时满足Izbash非线性定律，而高流速下满足达西渗流的结论[6]。RONG通过裂隙渗流试验，提出了考虑裂隙三维形态的非达西渗流方程[7]；ZOU通过数值模拟分析了剪切作用下粗糙裂隙的渗流特性[8]；ZHOU[9]通过大量的粗糙裂隙渗流试验，建立了基于裂隙参数的Forchheimer’s系数表达式。裂隙岩体的非线性渗流演化机理复杂，影响因素较多，关于应力作用下的裂隙非线性渗流有待进一步深入研究。岩溶地区的煤矿及隧道突水突泥事故频发，灰岩是岩溶地区主要的碳酸盐岩，因此开展裂隙灰岩的非线性渗流特征研究更具有代表性，对于揭示煤矿及隧道突水机理具有重要的理论与实际意义。本文通过开展不同粗糙度的裂隙渗流试验，研究了非线性渗流系数及渗透率与围压的关系，分析了水力开度与力学开度的演化规律，为研究孔裂隙介质渗流提供理论基础。

1 试验方法

1.1 裂隙岩样制备

本文试验对象为二叠系茅口组石灰岩，样品取自于湖南宁乡煤炭坝矿山中。岩样采集方向平行于层理方向。选取三个灰岩岩样M01、M02和M03进行渗流试验。样品采集后将其加工成直径50 mm、高100 mm的标准试件，并进行光滑处理。对打磨光滑的圆柱试样进行劈裂实验，形成不同裂缝形态的岩心试样，并通过文献[10]提出的裂隙面粗糙度测量方法，得到岩样M01、M02和M03的JRC值分别为8.96、13.3 和14.6。

JRC=32.2+32.471lgZ2

(1)

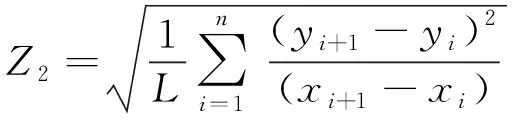
(2)

式中：JRC——粗糙度；

L——岩样长度；

xi、xi+1——分别为第i点和第i+1点的x方向坐标值；

yi、yi+1——分别为第i点和第i+1点的高度值。

1.2 裂隙隙宽测量

由立方定律可知，裂隙隙宽是决定渗透率大小的最重要因素之一。本文提出一种岩石裂隙开度测量的简单方法，具体步骤如下：

(1)采用水芯笔在岩样端面及侧面裂隙处每隔1 cm 作标记。

(2)将带有标准刻度的尺子(精确度0.1 mm)平行于裂隙安放，采用10倍放大镜对裂隙及1 mm刻度进行放大，并通过高清数码相机对放大后的标准尺及裂隙测点进行照相摄影。

(3)通过CAD软件对采集的图像进行放大，分别测量1 mm刻度的宽度及裂隙宽度，计算出裂隙宽度。

(4)重复进行步骤2及步骤3直至完成所有测点，裂隙隙宽取所有测点的平均值。

需要指出的是该方法主要用于测量微米级的裂隙宽度。

1.3 渗流试验程序

采用瞬态法对裂隙岩样进行了不同围压下的渗流试验。渗流试验在MTS815多功能岩石试验系统上进行。该实验系统由围压、轴压和孔隙流体压力三个自动伺服装置组成，最大围压和孔压可达到140 MPa，最大轴向压力为4 600 kN，可自动监测应力、位移、孔压等数据。

采用的瞬态法试验步骤如下：

(1)对制备好的岩样饱水24小时；

(2)将岩样安置在三轴腔内，连接上游、下游2个容器，以0.5 MPa/min 速率分别施加预设的围压及轴压荷载；

(3)在岩样上下游施加初始孔隙压力，并使试件内部和2个容器的孔隙流体压力达到平衡；

(4)保持出口端容器的流体压力不变，瞬时在进口端容器施加流体压力增量Δp，使两端产生孔隙压力梯度，从而引起流体在试样中流动；

(5)记录孔压随时间变化规律，直至达到平衡。施加下一级围压，重复步骤(4)进行下一组渗流试验。

2 试验结果分析

2.1 试验数据处理

大量研究表明裂隙中流体渗流满足Forchheimer定律[5，12]。对于一维的Forchheimer非达西渗流，流体速度与压力可表示为[13]

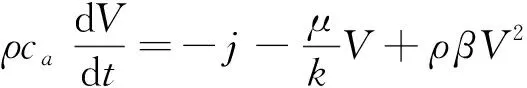
(3)

式中：ρ——流体密度；

ca——加速度系数；

V——渗流速度；

t——时间；

j——水力梯度；

μ——流体动力黏度；

k——渗透率；

β——非线性系数。

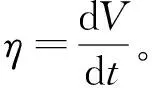
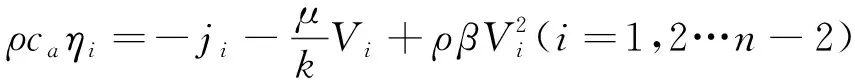
(4)

构造泛函数∏

(5)

由泛函数∏的极值条件，可解出非线性系数β及渗透率k。

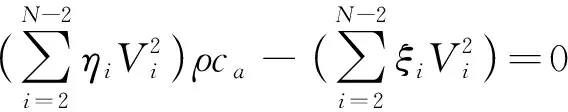
(6)

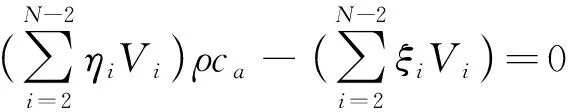
(7)

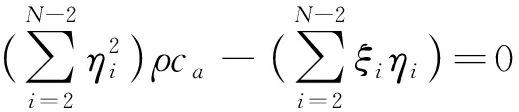
(8)

2.2 渗透率k与围压关系

图1(a)～(c)为岩样的渗透率与围压关系曲线. 由图可知，随着围压增加，岩样的渗透率先急速下降，再缓慢降低。这是由于围压增大，裂隙闭合度增大，但受裂隙面接触影响，裂隙闭合增量减小。对比图1(a)、图1(b)和图1(c)发现，在同一围压下，岩样渗透率M01>M02>M03，表明裂隙粗糙度越小，渗透率越大。为定量描述渗透率k与围压的关系，采用文献提出的幂数模型对试验数据进行拟合分析。

k=a1σcb1

(9)

式中：k——渗透率；

σc——围压，系数a1和b1为拟合系数。

图1(a)～(c)为试验数据和拟合曲线对比图。由图可知，二者吻合度较高，拟合系数均大于0.96，说明渗透率k与围压满足幂数函数关系。

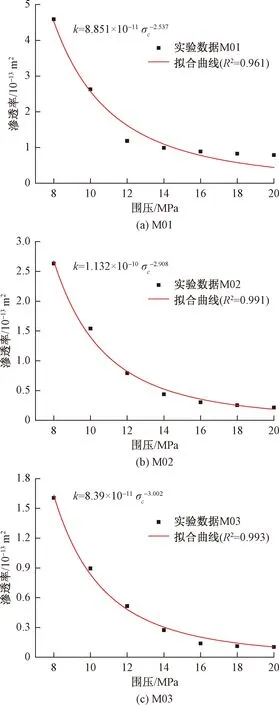
图1 渗透率与围压关系曲线Fig.1 Permeability k-confining pressure curves of sample

2.3 非线性系数β与围压关系

图2为非线性系数β与围压关系曲线。由图可知，随着围压增大，非线性系数逐渐增大，但增长速率变缓，说明围压越高，非线性效应越强。受岩样粗糙度的影响，在相同围压下，岩样M03的非线性系数最大，其次为M02，而M01岩样最小。说明粗糙度越大，越容易发生非线性渗流，这与文献实验结果一致。ZHOU认为裂隙表面越粗糙，越容易产生水力损失，因而非线性渗流越明显。MA[12]提出了对数函数来描述非线性系数β与围压的关系，

β=a2ln(σc)+b2

(10)

式中：σc——围压；

a2和b2——常数。

采用对数函数对本文试验数据进行拟合，如图2(a)-(c)所示。由图2可知，采用对数函数有偏差，其拟合系数均低于0.9。为此，本文提出新的经验关系式如下：

β=a3σcexp(λσc)+b3

(11)

式中：a3、λ、b3——常数。

利用新的函数关系对非线性系数与围压数据进行拟合。对于新的拟合函数，其拟合系数R2均大于0.99，说明新函数能更好的预测出非线性系数β与围压关系。

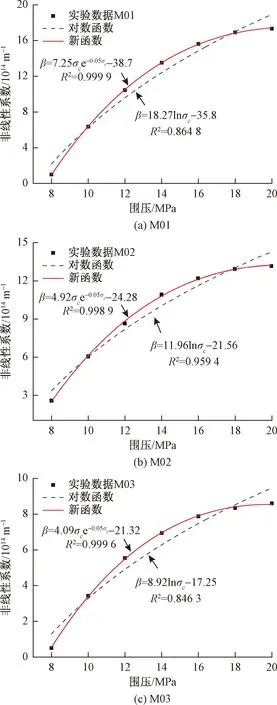
图2 非线性系数与围压关系曲线Fig.2 Non-Darcy coefficient-confining pressure curves of sample

2.4 裂隙变形

在渗流试验过程，围压压缩岩体裂隙导致裂隙闭合；孔压则导致裂隙张开，因此，裂隙岩体力学开度可计算为：

bm=b0-Δb1+Δb2

(12)

式中：bm——裂隙力学开度；

b0——裂隙初始开度，由2.2节裂隙隙宽测量方法得到；

Δb1——围压引起的裂隙闭合量；

Δb2——孔压导致的裂隙变形量。

围压作用下，裂隙岩体的变形可分为裂隙闭合和基质变形两部分。通过环向引伸计测量渗流试验过程岩样变形可得到裂隙的闭合量。根据VOGLER和ZHAO的试验研究[13-14]，围压引起的裂隙变形可由下式进行计算得到：

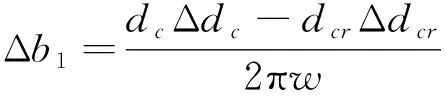
(13)

式中：w——裂隙宽度；

d——岩样截面周长；

Δd——围压引起的环向变形。

下标“c”和“cr”分别表示裂隙岩样和完整岩样。

图3为围压作用下的岩样环向变形图。由图可知，随着围压增大，岩样的环向变形接近线性增长，裂隙岩样的环向变形约为完整岩样变形的五倍。固定围压时，随着渗流时间增长，环向变形先迅速增长；随着孔隙压差的逐渐消散，变形逐渐趋于稳定，如图4所示。通过测量环向变形数据，由式(13)计算出裂隙力学开度。

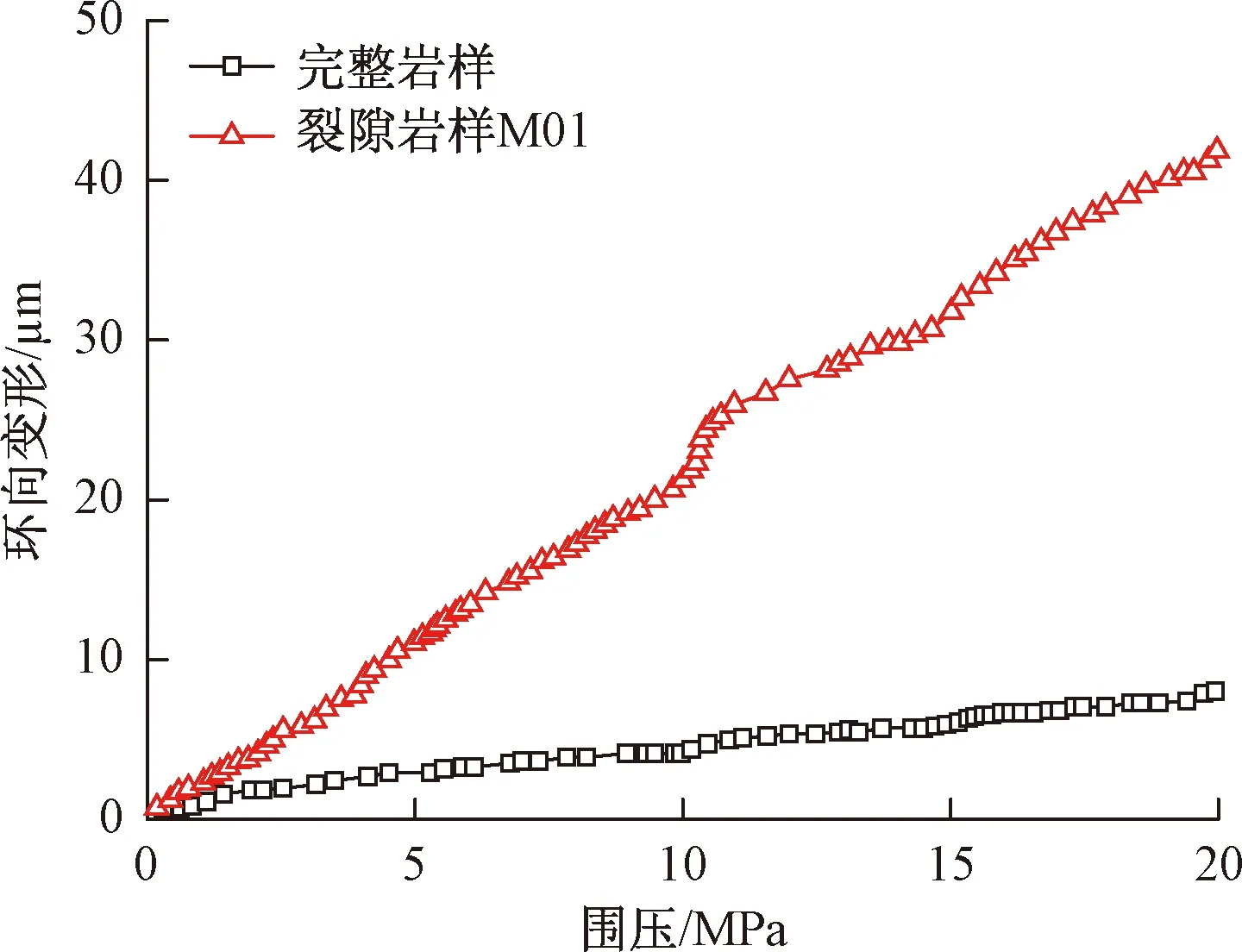
图3 完整岩样和裂隙岩样M01的环向变形Fig.3 Circumferential deformation of intact sample and fractured sample (M01)

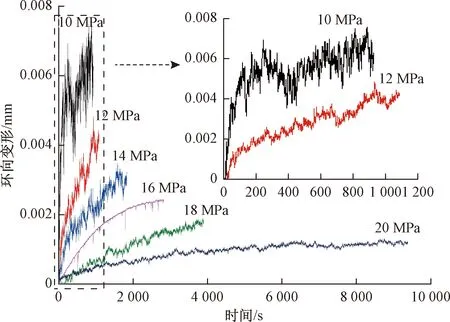
图4 渗流过程裂隙岩样M01环向变形Fig.4 Circumferential deformation of sample M01 during transient pulse test

由立方定律，可计算得到裂隙渗流的水力开度：

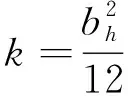
(14)

式中：bh——水力开度。

图5为力学开度与水力开度的对比图。由图可知，随着围压增加，岩体力学开度与水力开度均呈下降的趋势。且裂隙水力开度均小于力学开度，水力开度约为力学开度的5%，这与前人的研究结果一致[7]。

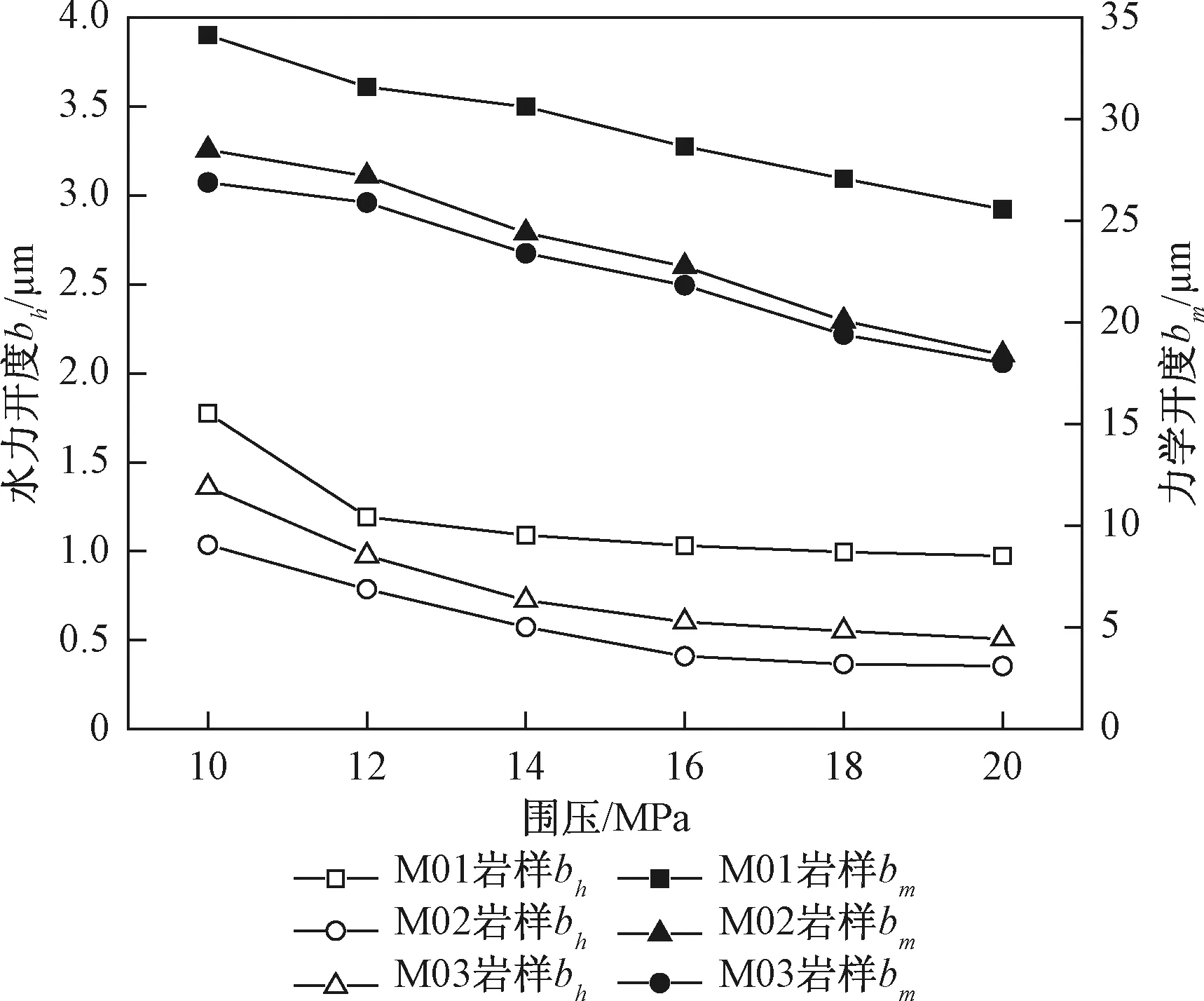
图5 水力开度与力学开度Fig.5 Hydraulic aperture and mechanical aperture

3 结论

本文开展了不同粗糙裂隙的渗流试验，研究了裂隙灰岩的非线性渗流系数及渗透率与应力关系，得出主要结论如下：

(1)提出了一种简便的裂隙隙宽测量方法，操作简单，经济可靠。

(2)随着围压增加，岩样的渗透率先急速下降，再缓慢降低，二者满足幂数函数关系。

(3)随着围压增大，非线性渗流系数β逐渐增大，但增长速率变缓，基于试验数据提出了非线性渗流系数与围压经验关系式；裂隙越粗糙，非线性效应越强。

本文试验在灰岩条件下进行，对于其它类裂隙岩体的非线性渗流特征有待于进一步深入研究。