表贴式永磁同步电机磁极不对称化齿槽转矩削弱方法
2020-08-27贠剑虹娄幸媛
贠剑虹,娄幸媛,梁 爽
(陕西省水利电力勘测设计研究院, 陕西 西安 710001)
永磁同步电机具有功率密度高、效率高、结构简单、可靠性高、功率因数高等优点,在工业、农业、水利、航空航天等领域具有广泛应用,可用作驱动电机、发电机、励磁机等[1-4]。
随着几年来稀土永磁材料的不断发展,永磁材料的剩磁、磁能积等性能不断提升,高性能稀土永磁材料提升永磁电机性能的同时,也使永磁电机的齿槽转矩大幅增加,带来振动、噪声等问题。对于部分应用场合的永磁同步电机,例如高精度伺服电机,削弱齿槽转矩有助于提高电机的驱动精度;对于大型永磁同步发电机,例如水力发电永磁主励磁机,减小齿槽转矩可降低发电机的振动,提高设备运行的安全性。
目前永磁同步电机齿槽转矩削弱方法主要是通过定子以及转子结构的优化。定子结构优化主要包括定子斜槽、槽口优化、分数槽、磁场调制的齿槽优化等方法[5-10]。转子优化是当前齿槽转矩优化的主要手段,主要包括极弧系数优化、磁极形状优化、磁极偏移、磁极分段和开辅助槽等。有学者提出不等厚永磁体以及不等厚气隙减小永磁同步电机齿槽转矩的方法,该方法通过优化永磁体厚度或气隙厚度,使气隙磁密波形接近正弦,减小谐波含量,使齿槽转矩得到降低[14-15]。该方法中永磁体加工困难,需要引入附加的成本。文献[16-18]提出基于转子磁极偏移齿槽转矩削弱方法,并通过解析计算确定永磁体的偏移角度,该方法能够确定磁极偏移角度。张昌锦等还提出一种通过转子齿偏移来削弱齿槽转矩的方法,并通过增大齿宽以补偿由于转子齿偏移带来的转矩减小的问题[19]。文献[20]针对表贴式永磁同步电机存在的齿槽转矩问题,提出一种在电机转子轴向组合不同永磁体的齿槽转矩削弱方法,该方法简单易实现,同样会增加工艺复杂度。另外有学者对每极两块、每极三块Halbach 永磁阵列中主磁钢弧角和辅磁钢充磁方向角对电磁转矩与齿槽转矩的影响,对比分析径向充磁、平行充磁和Halbach永磁阵列的永磁电机电磁转矩与齿槽转矩随永磁体厚度的变化规律[21]。磁极偏移以及转子齿偏移均会导致加工难度的增加。有学者提出在现有电机基础上进行转子在设计优化以减小尺寸转矩的方法,文献[22]中提出了单一极内偏心槽、组合偏心槽、磁桥优化的递进再设计方法,以一种车用永磁同步电机为研究对象,在对偏心槽和组合偏心槽对齿槽转矩和谐波转矩影响分析的基础上,进行磁桥再设计,达到削弱齿槽转矩的目的,该种方法是局部尺寸小幅调整,齿槽转矩优化并不彻底。通过优化表贴式永磁电机磁极宽度也可实现齿槽转矩的削弱,极弧系数的变化将导致反电动势波形以及转矩大小的变化[23-26]。文献[27]中提出一种不对称的V 型永磁体结构,用以减小内嵌式永磁同步电机的齿槽转矩,取得了良好效果。
综合当前齿槽转矩削弱方法研究现状,拟对转子磁极宽度进行优化,在保证电机总磁通一定条件下,提出一种基于不对称磁极极弧宽度优化削弱永磁同步电机齿槽转矩的方法,通过不对称磁极结构气隙磁场分析、齿槽转矩计算、齿槽转矩削弱原理分析,计算出最优磁极宽度,通过有限元仿真验证所提不对称磁极方法的齿槽转矩削弱效果。
1 齿槽转矩磁导分析模型
以一种极对数p=4、槽数z=24的表贴式永磁同步电机为例进行分析,建立如图1所示磁导分析模型:磁通经过的闭合磁路构成磁导单元,共4个磁导单元,分别为单元1、单元2、单元3、单元4。

图1 磁导分析模型
单元i(i=1,2,3,4)的齿槽转矩为:
(1)
式中:fi为单元i的磁动势;Λj为单元i磁导j次谐波的幅值;θ0i为不同单元磁导谐波的相位差。
电机总齿槽转矩由各单元齿槽转矩合成,对于该4极电机,磁极对称,故每个单元的齿槽转矩幅值相同,而相位不同。由式(1)可知,齿槽转矩只包含z的倍数次谐波。对于n(n=1、2、3…)次谐波,各单元的齿槽转矩相位差为12nπ,相位相同。
2 不对称磁极结构及其磁场分析
以一种p=4、z=24表贴式永磁同步电机为例说明不对称(极弧不等宽)磁极结构,图2(a)为对称结构,各极的极弧宽度θa均为82°;图2(b)为不对称结构,调整图2(a)中磁极PM1的极弧宽度至θb1,为保持总的磁钢用量不变,保持极间宽度θc(图中为8°)不变,其它磁极(PM2、PM3、PM4)的极弧宽度相等:θb2=θb3=θb4,图2(b)中调整后PM1极弧宽度为94.9°,PM2、PM3、PM4的极弧宽度为77.7°,此时4个极的极弧宽度不对称,转子沿PM1、PM3的平分线左右对称。用磁极不对称率k表示磁极不对称程度:
k=θb1/θb2
(2)
k即磁极大极的极弧宽度与小极极弧宽度的比值,且有k≥1。
对图2(b)中的不等宽磁极结构进行分析,为简化分析模型,做以下假设:(1) 定转子铁心磁导率为无穷大;(2) 磁钢与空气的磁导率相同;(3) 各极磁钢材料相同。建立如图3所示的磁路分析,磁通通过PM1与PM2的磁路定义为磁路单元1,通过PM2和PM3的磁路定义为磁路单元2。

图2 对称与不对称磁极结构
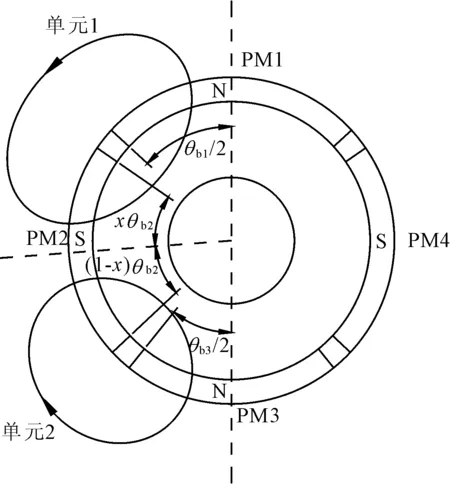
图3 磁路分析模型
图3所示转子沿PM1和PM3的中线左右对称,单元1中PM1极弧宽度θ1.1=θb1/2,PM2极弧宽度为θ1.2=xθb2,x为小于1的常数;单元2中PM2极弧宽度θ2.1=(1-x)θb2,PM3极弧宽度θ2.2=θb3/2。为便于计算,对极弧宽度做归一化处理,所有极弧宽度均除以θb2,则各单元各磁极极弧宽度处理为:θ′1.1=0.61,θ′1.2=x,θ′2.1=1-x,θ′2.2=0.5。
PM2空载等效磁路如图4所示,图中Fc=Hc·hm,Hc为磁钢矫顽力,hm为磁钢厚度;Rm表示PM2内部磁阻;Φ表示PM2的总磁通,Φ1、Φ2分别表示通过单元1和单元2的磁通;R1、R2分别表示单元1和单元2磁路的磁阻。
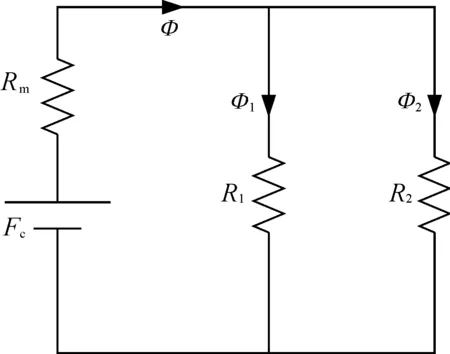
图4 不对称磁极单极下等效磁路
由图4中的两条并联支路磁压降相等,可得出:
Φ1·R1=Φ2·R2
(3)
根据同一磁极下磁密相等、磁通与面积成正比的条件,结合式(3),可得出:
(4)
磁阻R1、R2取决于气隙和磁钢的尺寸与参数,单元1、与单元2的轴向长度L、磁导率μ相等,故R1、R2只取决于磁通经过的气隙和磁钢的面积,单元1和单元2磁通经过的磁钢和气隙面积分别为S1、S2,则有:
(5)
由式(4)、式(5)可以得:
(6)
根据图2给出的算例参数,S1/S2=1.22,进而可得x=0.55,θ′1.2=0.55,θ′2.1=0.45。通过单元1中PM1和PM2的磁通相等,通过的面积分别为Cθ1.1、Cθ1.2(C为常数),PM1、PM2下气隙磁密B1、B2分别为Φ′/Cθ1.1、Φ′/Cθ1.2,故B1/B2=0.9,同样有,B3/B2=0.9,可得:B1=B3=0.9B2,转子磁路左右对称,则有:B2=B4=1.11B1。该不等宽磁极结构不同极性磁极下的磁密不等,同极性磁钢下磁密相等。用磁路法作PM2空载工作点,可求得PM2的气隙磁密B2=0.853 T,进而得出B1=B3=0.768 T,B2=B4=0.853 T。
对于极对数p的不等宽磁极电机,假设PM2单元1部分宽度为x,利用磁路模型可以推导可得:
(7)
由式(4)—式(7)可得:
(8)
由式(8)可知,B1/B2的比值小于1,随p的增加而增加趋近于1,说明可通过增加极对数的方式以降低磁密幅值的不对称性。
将不对称磁极结构电机进行有限元仿真,仿真磁密线分布图如图5(a)所示,由图可知不对称磁极结构的磁密线分布不对称。磁密波形如图5(b)所示,图中横坐标表示沿气隙的圆周的距离,纵坐标表示磁密的绝对值。由图5(b)可以看出,磁密波形高低相间,同极性的磁钢磁密相等,不同极性磁极磁密不等。仿真结果为:B1=B3=0.756 T,B2=B4=0.833 T。有限元仿真结果与磁路法分析结果基本一致,证明了所提解析模型的准确性。

图5 不对称四极永磁电机磁场仿真结果
3 不对称磁极结构的齿槽转矩分析
磁极结构优化后,各磁导单元位置发生了偏移,各单元齿槽转矩相位相应发生改变,相比优化前,各单元齿槽转矩的谐波分量相位不再相同,k取特定值时,可使各单元齿槽转矩的谐波分量相互抵消,从而使电机齿槽转矩得到削弱。
在磁极不对称条件下,对于24次谐波,用tcogi.24表示单元i齿槽转矩的24次谐波分量,当不对称角度达到一定程度时,齿槽转矩矢量分布图如图6(a)所示,此时不同磁极的齿槽转矩可相互抵消。用tcogi.48表示单元i齿槽转矩的48次谐波分量,此时齿槽转矩矢量分布图如图6(b)所示。对于各单元齿槽转矩24的奇数倍数次谐波分量,分布情况与36次谐波相似,四个分量两两相差90°,且tcog1.n与tcog3.n、tcog2.n与tcog4.n总在相反方向上;对于24的偶数倍数次谐波分量,分布情况与48次谐波相似,4个分量处在两个方向,tcog1.n与tcog4.n、tcog2.n与tcog3.n始终反向。

图6 各单元齿槽转矩谐波分量矢量分布图
磁极不对称(不等宽)使各单元磁导不同,其中单元1与单元4、单元2与单元3的磁导相同,前者大于后者,有tcog1.n=tcog4.n>tcog2.n=tcog3.n,根据矢量分布图可知,磁极优化可完全消去24的偶数倍数次谐波分量,不能完全消去24的奇数倍数次谐波分量,所以本文的磁极不等宽优化方法不能完全消除电机的齿槽转矩,但可大幅削弱齿槽转矩。
对于任意p对极电机,磁极对称时极弧宽度为θa,单元1与单元2、单元2与单元3…单元2p-1与单元2p的空间位置相差Δθ:
(9)
以24槽4极的永磁同步电机为例进行计算,齿槽转矩的谐波分量相位相差24n·Δθ,要使各单元的齿槽转矩相互抵消,需要满足24·Δθ=π/2或24·Δθ=3π/2,则有24·Δθ=π。为避免过多地调整磁钢宽度对电机性能造成影响,k应尽可能小。将p=4代入式(9),可得出使齿槽转矩最小的最优k值,计算得出最优k值为1.26。
4 有限元分析仿真
利用有限元分析软件对该24槽4极永磁同步电机k值变化时齿槽转矩变化趋势,仿真结果如图7所示,由仿真结果可知,当k=1.30时电机的齿槽转矩最小,与解析计算最优值1.26的误差为3.1%。

图7 不同k的仿真齿槽转矩
当k=1.30时,有限元仿真齿槽转矩幅值为0.011 N·m,磁极优化前(对称磁极,k=1.00)齿槽转矩幅值为0.126 N·m,磁极优化前后的齿槽转矩波形见图8,通过磁极不对称优化,可使永磁同步电机的齿槽转矩减小91.3%,齿槽转矩得到大幅降低。

图8 磁极优化前后齿槽转矩波形对比
5 结 论
本文针对永磁同步电机的齿槽转矩问题,提出了一种基于磁极不对称化设计的齿槽转矩削弱方法,该结构具有易实现、工艺简单等优点。通过不对称磁极气隙磁场的计算与仿真,分析了不对称磁极对齿槽转矩的削弱原理,准确计算出最优的磁极不对称率,使齿槽转矩达到最小,有限元仿真结果表明,最优不对称率计算值与仿真值的误差为3.1%,优化后齿槽转矩减小了91.3%。
