非饱和土一维渗流与变形耦合问题的数值分析
2020-08-27赵思同高国耀周凤玺
赵思同, 高国耀, 周凤玺
(1.甘肃省交通规划勘察设计院股份有限公司, 甘肃 兰州 730050;2.兰州理工大学 土木工程学院, 甘肃 兰州 730050)
与饱和土不同,非饱和土中不仅有固相和液相,而且还有一定量的气相存在,它广泛存在于干旱、半干旱地区和地下水位以上的土体中。对非饱和土渗流和变形问题的研究在解决工程实践中经常遇到的地基沉降变形、渗透破坏等有着十分重要的意义,如地基渗流与变形,降雨引起的边坡失稳、垃圾填埋的处理等[1-2]。
由于土体中的应力场和孔隙流体压力分布影响着土骨架的变形,与此同时,土体孔隙特征的改变将会引起流体渗透相关参数的变化,进而影响土体中渗流场的分布。可见,非饱和土的应力场、渗流场和位移场是相互影响,相互作用的。因此,很有必要采用渗流-变形(流-固)耦合的方法对非饱和土的力学行为进行研究。
国内外学者关于非饱和土的渗流与变形问题研究已有许多的理论成果。徐炎兵等[3]基于多孔介质力学原理,建立能模拟非饱和土两相流动与变形耦合问题的理论模型,利用Galerkin法对控制方程进行离散,得到控制方程的有限元计算格式,并验证了所提出的分析方法在模拟非饱和土渗流以及变形问题时的有效性,从而为定量研究饱和-非饱和渗流以及变形问题提供了一条有效途径;吴礼舟等[4]通过Fourier积分变化,考虑了任意初始的孔隙水压力分布和流量边界条件,研究表明变形与渗流耦合对非饱和土中水的入渗产生重要的影响,进一步分析了耦合解的各个参数的影响;唐凯等[5]运用非饱和土渗流理论对边坡进行渗流场和应力场耦合分析;Olivella等[6]、Thomas等[7]分别从水-气-热三场耦合的角度分析了多孔介质孔隙中各个组分的渗流与变形问题;Schrefler[8]在Zienkiewicz等[9]的理论模型基础上,分析了非饱和土孔隙介质中湿相与非湿相两相渗流与变形问题;秦冰等[10]基于混合物理论,推导了在气压力变化条件下水与水蒸气相变平衡所满足的限制方程;胡冉[11]开展了非饱和土水力全耦合本构模型及数值模拟方法等内容的研究。然而由于非饱和土中流-固耦合问题的复杂性,到目前为止,无论是数学模型的描述还是数值求解方法的有效性方面尚不完善。
基于多孔介质理论,考虑固-液-气三相耦合的情况,在耦合过程中考虑了孔隙中溶液、溶解在水中的气相、气相中的水分、干燥气体等组分,建立了非饱和土多孔介质中固相、液相、气相三相耦合的数学模型。考虑一维非稳态问题,利用Laplace积分变换,选取孔隙气压力、孔隙水压力和土颗粒位移以及它们的一阶导数作为状态变量,得到了问题的状态方程组。在给定的边界条件下,结合打靶法和数值Laplace逆变换求解了该耦合的非线性变系数微分方程组,并通过与已有的试验结果相比较,验证了模型的有效性。该研究结果将对非饱和土渗流与变形耦合问题理论与数值分析研究提供一定的参考价值。
1 基本方程
分别以s,l,g表示非饱和土中的固相骨架、孔隙液相和孔隙气相。考虑土体的孔隙率为n,孔隙被液相和气相共同填充,体积分数分别为φl和φg,则有n=φl+φg。孔隙液相由液态水和溶解的气体两种组分组成,气相由水蒸气和干燥气体组成。非饱和土各相以及各组分构成如图1和表1所示。

图1 非饱和多孔介质的示意图

表1 非饱和多孔介质中的各相组成
1.1 物理方程
非饱和土有效应力公式为:
(1)

φl=nSl,φg=nSg,Sg+Sl=1
(2)
基于弹性小变形假设,利用几何方程可得到土体的物理模型为:
(3)
式中:G和K分别为土体的剪切模量和体积模量;ui为土骨架位移分量。
1.2 质量守恒方程
组分α(α=w,a分别代表水分、干燥气体)在π相(π=l,g分别表示液相和气相)中的质量守恒方程可表示为[12-14]:
(4)
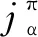
1.2.1 水分质量守恒
由于水分主要存在于液相和气相中,忽略固体颗粒中的水分含量,结合式(1)和式(4),可得:
(5)
(6)
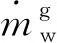
(7)
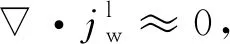
(8)
基质吸力Pm与饱和度的关系可表示为:
Pm=Pg-Pl=PdSe-1/ϑ
(9)

考虑土体骨架位移速率的散度与体积应变率的关系[15]:
(10)
由固相质量守恒方程可得:
(11)
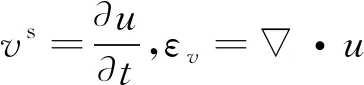
引入平均相对速度[16]:
(12)
(13)
根据广义达西定律,液相和气相的对流通量分别表示为[15]:
(14)
qg=-Kg(Pg+ρgg)
(15)
式中的各参数表达式如下[15]:

1.2.2 干燥气体质量守恒
假设气体仅存在于气相中,不考虑固相中的干燥气体。结合式(5)和式(4)可得:
(16)
(17)
1.3 动量守恒方程
多孔介质的动量守恒方程为:
·σ+f=0
(18)
式中:σ为总应力;f=g[(1-n)ρs+nSlρl+nSgρg]为体积力。
根据有效应力原理式(1)和物理方程式(3),结合方程式(18)可得到三相耦合的动量守恒方程:
(19)
2 一维非稳态问题的控制方程
通过对基本方程式(8)—式(19)进行理论推导,最终得到的以孔隙水压力Pl、孔隙气压力Pg和骨架位移u为基本未知数的非饱和渗流-变形耦合问题的控制方程:
(20)
ρaSg∂tu,i-ρaKg(Pg,ii+ρgg)-
(21)
g[(1-n)ρs+nSlρl+nSgρg]=0
(22)

考虑一维问题,并应用Laplace积分变换即可得到频域内问题的控制方程为:
(23)
(24)
g[(1-n)ρs+nSlρl+nSgρg]=0
(25)
(26)

方程式(25)是一个多物理场耦合的变系数偏微分方程组,一般很难获得其解析解答,而打靶法是一种求解强非线性微分方程的有效方法[17-18]。求解时使用Runge-Kutta和Newton-Raphson方法不断调整初值参数,使得初值参数的解适用于终点边界条件,从而得到原边值问题的频域上的精确解。为了获得时间域上的结果,基于矩方法的稳定化算法,通过Hausdoff矩方法将其进行数值逆Laplace变换[19]。
3 数值算例


表2 非饱和土的边界条件
其中,孔隙水压力和孔隙气压力的值为相对大气压力。
3.1 Liakopoulos试验的数值模拟
根据Liakopoulos[20]等提供的土样参数,选取如表3所示的非饱和土物理力学参数进行了数值模拟。图2给出了在重力作用下土体中水压力模拟值与Liakopoulos的试验值的对比结果,可以看出两者变化基本一致。

图2 水压力试验结果与模拟结果对比

表3 Del Monte砂土的材料物理力学参数
在与Liakopoulos试验相同的边界条件下,图3—图5分别给出了土体不同位置处孔隙水压力,孔隙气压力和位移随时间的变化情况。由图3可知土体底部的孔隙水压力随着时间的增大而逐渐减小,大概在120 min后,孔隙水压力的变化逐渐趋于缓和,这是因为随着时间的增长,最后土柱在底部排水作用下孔隙水压力逐渐趋于稳定。由于气体可以自由进入土柱顶部边界,使得土柱试样下部的气压变化率明显慢于试样上部的砂样。从图4可以看出,随着时间的不断增大,孔隙气压力的变化率不断减小,最后孔隙气压力逐渐趋于缓和,这是因为随着时间的增大,土柱试样顶部的气体不断进入土柱内,使得气压与大气压的值逐渐接近。由图5可以看出土柱试样在不同高度处的竖向位移随着时间的变化逐渐增大,但是大概在120 min后,竖向变形逐渐趋于缓和,这是因为随着时间的变化,土柱试样在重力作用下竖向固结逐渐趋于稳定。

图3 不同位置处孔隙水压力的变化

图4 不同位置处孔隙气压力的变化
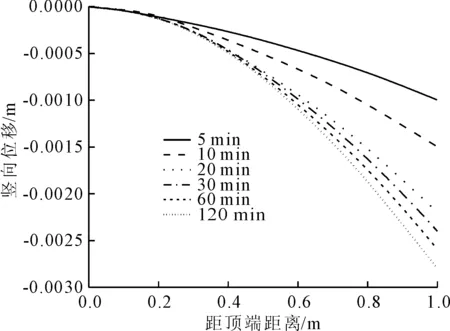
图5 不同位置处竖向位移的变化
对比Liakopoulos的试验数据结果可以得知,本文提出的渗流与变形耦合分析的数值模型在理论数值分析上基本反映了非饱和土体内液相与气相的存在状态,同时也较为准确地反映了气-水两相流动变化与土骨架位移变形之间的相互影响关系。
3.2 参数分析
为了进一步研究非饱和土中水-气-土骨架颗粒三相耦合的过程,对不同孔隙率、孔隙水压力、渗透系数等条件下的孔隙气压力的变化规律进行了参数分析。
为了分析土体孔隙率对非饱和土体中流-固耦合的影响,图6—图8分别给出了土体上下边界的孔隙气压力均为0 kPa,土体上边界孔隙水压力为0 kPa,下边界孔隙水压力分别为-20 kPa,土体孔隙率分别为0.3、0.4、0.5条件下,土体不同位置处孔隙气压力、孔隙水压力以及饱和度随时间的变化情况。从图中可以看出土体中的孔隙气压力的分布趋势基本保持不变,但是随着土体中孔隙率的增加,土体中的孔隙气压力逐渐降低。随着土体孔隙率的增大,土体中孔隙水压力随时间而逐渐增大,当土体的孔隙率较大时土体孔隙中的水分迁移越快,即土体底部在相同时间下土体水分饱和度越大。

图6 不同孔隙率下孔隙气压力的变化

图7 不同孔隙率下孔隙水压力的变化
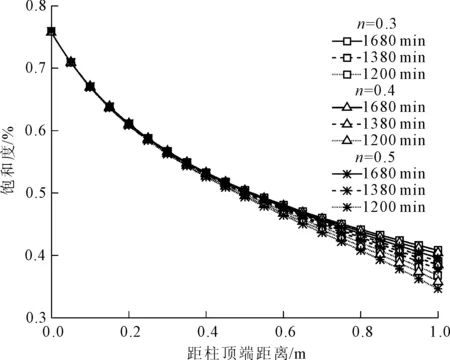
图8 不同孔隙率下饱和度的变化
当土体孔隙率为n=0.3,上下边界的孔隙气压力均为0 kPa,土体上边界孔隙水压力为0 kPa时,图9给出了下边界的孔隙水压力分别为-8 kPa、-9 kPa、-10 kPa的条件下,土体中孔隙气压力的分布情况。从图9中可以明显地看出,随着下边界孔隙水压力的减小即土体饱和度的减小,土体中孔隙气压力的分布趋势基本保持不变,即孔隙气压力在土体内部会增大使其大于土体边界处的孔隙气压力。随着土体孔隙中水分饱和度的减小,相同时间条件下土体孔隙中的孔隙气压力随之减小。
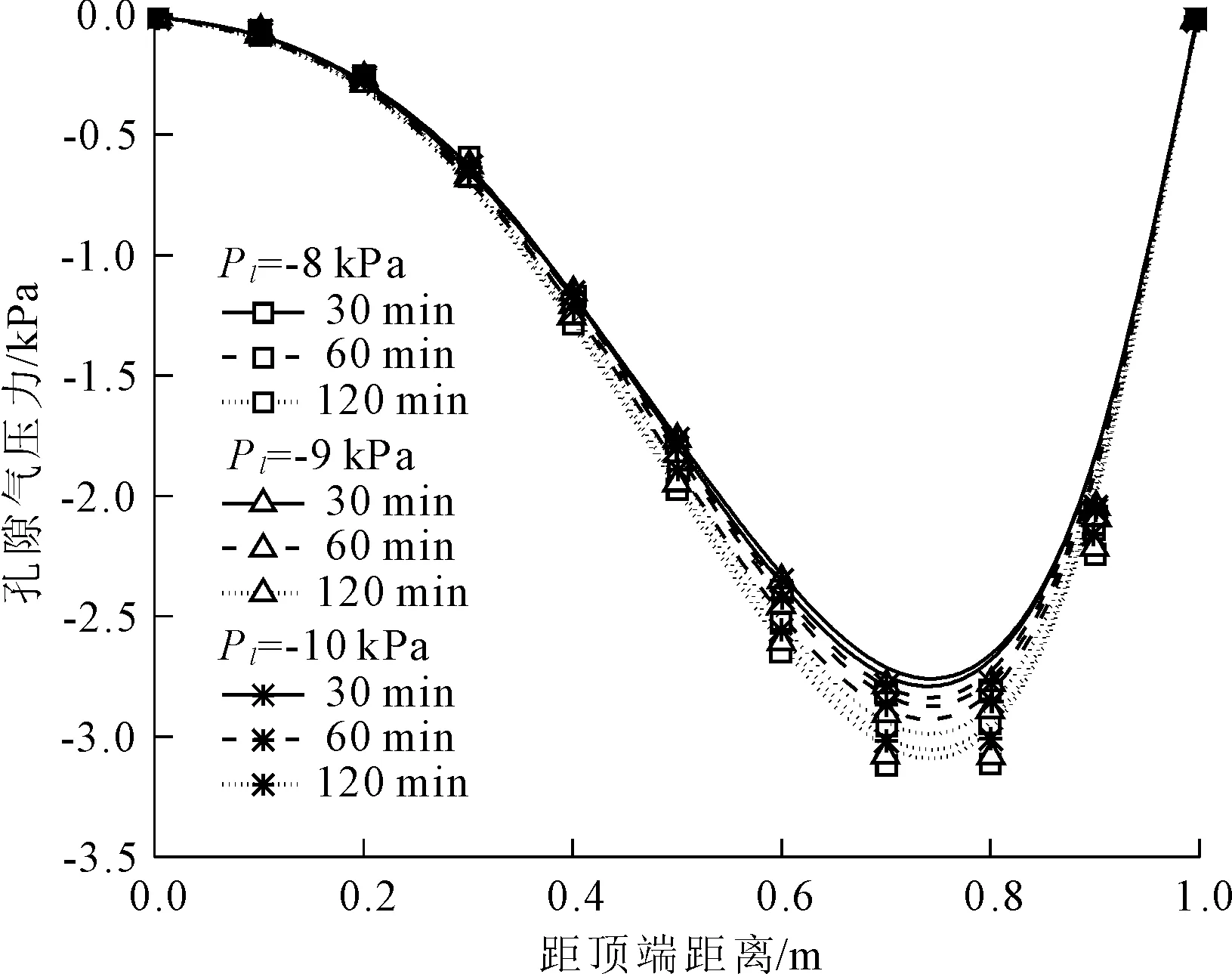
图9 不同孔隙水压力下孔隙气压力的变化
当土体孔隙率为n=0.3,上下边界的孔隙气压力均为0 kPa,土体上边界孔隙水压力为0 kPa,土体下边界的孔隙水压力为25 kPa时,图10、图11分别给出了土体的渗透系数分别为8.6×10-6m/s、5.6×10-6m/s、2.6×10-6m/s的条件下,土体中孔隙水压力和饱和度的变化情况。由图10、图11可以明显地看出,随着土体渗透系数的减小,在相同时间条件下土体中的孔隙水压力而逐渐减小,即随着土体渗透系数的减小土体中水分的迁移能力而逐渐减弱,即在相同时间条件下土体底部水分的饱和度随着渗透系数的增大而随之逐渐增大。
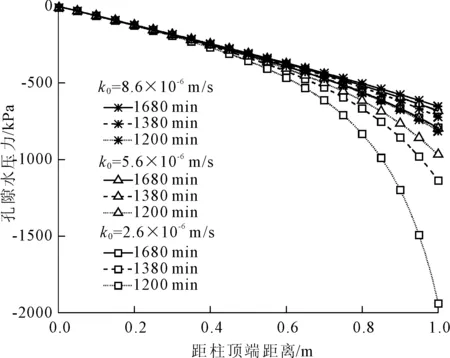
图10 不同渗透系数下孔隙水压力的变化

图11 不同渗透系数下饱和度的变化
4 结 论
基于多孔介质理论,建立了等温条件下非饱和土多孔介质中水分、气体、骨架位移等多场耦合的数学模型。在求解非线性耦合方程时选取孔隙水压力、孔隙气压力、土骨架位移、时间以及它们的一阶导数变化作为状态变量,采用打靶法进行数值分析。通过与已有的试验结果相比较,验证了模型的有效性。结果表明:
(1) 非饱和土体中水、气两相的渗流变化是相互影响的,并且与土体的变形相互作用。
(2) 土体孔隙率的变化对相关物理量的变化有着显著影响。随着孔隙率的增大使得土体气相和液相渗透系数的增加,从而使土体中孔隙气压力降低。
