微透镜阵列的慢刀伺服加工表面粗糙度预测模型

林泽钦 陈新度 颜志涛 孙豪

摘 要：建立了超精密加工微透镜阵列的表面形貌预测模型。基于切削参数、刀具几何参数、微透镜阵列的几何结构，分析了加工的軌迹规划;模型中考虑了刀具与工件之间三维方向相对振动的影响，仿真出加工的表面形貌和粗糙度。通过仿真模型的计算，分析了切削参数、透镜几何参数对微透镜阵列表面形貌及粗糙度的影响。

关键词：微透镜阵列;慢伺服加工;轨迹生成;振动;表面预测

DOI：10.15938/j.jhust.2020.03.013

中图分类号： TH161.1

文献标志码： A

文章编号： 1007-2683（2020）03-0083-05

Abstract：A prediction model for the surface topography generation in the ultra-precision machining of microlens arrays is established. The tool path generation is analyzed based on the cutting parameters， tool geometry parameters and geometry of microlens array. The tool-work vibrations in three dimensional directions are considered in the model to simulate the surface topography and predict the roughness. The influence of cutting parameters and lens geometric parameters on the surface topography and roughness of microlens array is studied through the simulation model.

Keywords：microlens array; slow tool servo cutting; tool path generation; vibration; surface prediction

0 引 言

在现代光学系统中，微结构阵列表面得到广泛应用，包括微透镜阵列、微棱镜阵列、微柱面槽、正弦波微槽、微 V 形槽等在内的微结构光学元件具有体积小、质量轻、集成度高、造价低等优点，能实现特定的光学功能，提高光学系统的性能，精简系统的结构[1-3]。其中，微透镜阵列光学元件广泛应用在均匀照明、光束聚能及整形、光学波前检测、光场相机等光学系统中。

针对微透镜阵列元件的生产制造，精密加工技术提供了整体一次加工的实现方法[4]，不需要抛光等后续加工就可以使加工精度达到亚微米级的形状精度和纳米级的表面光洁度。其中，超精密车削加工有快刀伺服（fast tool servo， FTS）车削和慢刀伺服（slow tool servo， STS）车削技术。快刀伺服车削技术中使用了由压电陶瓷、音圈电机等元件驱动的辅助刀架，进行高频的快速精密进刀运动，实现复杂面形的加工，但大多数快刀装置行程有限，一般小于1mm，且驱动元件的滞后问题会造成跟踪性能下降，主轴位置估计误差会引起加工轮廓混淆[5]。慢刀伺服车削技术是在超精密加工机床上使用主轴的精密位置伺服控制模式（C轴模式），采用C、X、Z三轴联动方式进行加工，不需要额外的刀具驱动装置，广泛应用于复杂曲面的加工。使用慢刀伺服技术车削微透镜阵列，其加工的表面形貌和粗糙度与加工过程中的多个因素相关，比如刀具几何尺寸、加工参数、加工面几何参数、刀具路径规划、主轴回转误差、材料特性、刀具与工件之间的振动、刀具磨损等等。国内外有多个团队对上述因素进行了研究，并提出相关预测模型[6-8]。

本文研究了慢刀伺服加工微透镜阵列的刀具切削轨迹规划过程，考虑加工参数、刀具几何参数、透镜阵列几何参数，以及刀具与工件在三维方向的振动等因素的影响，提出微透镜阵列慢刀伺服加工的表面预测模型。

1 微透镜阵列超精密加工的轨迹规划

利用超精密加工机床CXZ轴的精密位置联动控制功能，慢刀伺服车削可实现微透镜阵列的加工。在加工过程中，刀具相对于工件的加工轨迹在XY平面的投影是螺旋线（图2），机床的Z轴则根据微透镜阵列的几何面形以及C轴反馈的位置信号，带动刀具进行进刀切削运动。在进行加工前，需要根据微透镜阵列的几何面形、刀具几何尺寸、加工参数等规划加工切削的轨迹，生成CXZ三轴的联动加工代码。

1.1 切削轨迹生成

以主轴的换转中心点为原点构建极坐标系，在极坐标系下的慢刀伺服切削的轨迹可用下式表達：

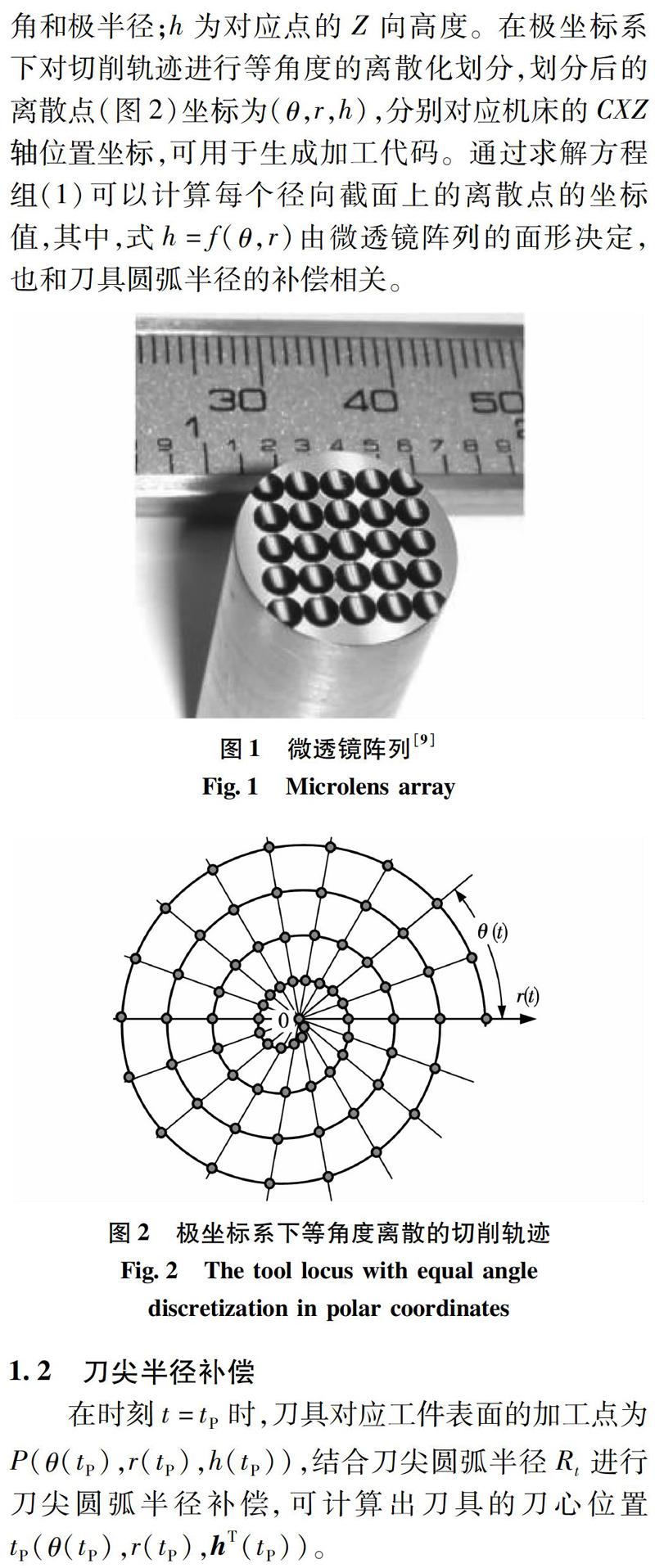
式中：n为主轴转速（r/min）;Rw为加工工件尺寸（mm）;F为X轴的进给速度（mm/min）;t为加工时间（s）;q和r分别是刀心位置点在极坐标系下的极角和极半径;h为对应点的Z向高度。在极坐标系下对切削轨迹进行等角度的离散化划分，划分后的离散点（图2）坐标为（θ，r，h），分别对应机床的CXZ轴位置坐标，可用于生成加工代码。通过求解方程组（1）可以计算每个径向截面上的离散点的坐标值，其中，式h=f（θ，r）由微透镜阵列的面形决定，也和刀具圆弧半径的补偿相关。

1.2 刀尖半径补偿

在时刻t=tP时，刀具对应工件表面的加工点为P（θ（tP），r（tP），h（tP）），结合刀尖圆弧半径Rt进行刀尖圆弧半径补偿，可计算出刀具的刀心位置tP（θ（tP），r（tP），hT（tP））。

刀尖圆弧半径补偿的方法有2种，一种是沿轮廓法线方向的补偿，另一种是沿Z轴方向的补偿。法线方向的补偿即刀具沿着当前工件加工点所在曲线的法线方向偏置距离Rt，这在实际加工中需要机床的X轴和Z轴联动以实现这个补偿偏置量。因此，X轴除了完成进给运动外，需要有额外的微小移动，而由于一般机床X轴上安装有主轴、Y轴结构，负载重量大，动态性能差，采用这种补偿方式会限制加工的速度。本研究采用了Z轴方向的补偿方法，在加工过程中X轴保持固定的进给速度，刀具通过Z轴方向的偏置使得刀尖圆弧与工件表面相切（图3），Z轴偏置量与轮廓上该点的曲率半径有关，刀尖触点Pcut的连线在XY平面的投影则不是标准的螺旋线。采用这种补偿方式，偏置补偿运动由Z轴实现，而Z轴负载较小、动态响应能力相对较高，加工的稳定性更高。设工件截面轮廓为LP，补偿后的刀路轨迹Lt可表示如下：

式中：nP为与曲线各点曲率半径相关的偏置系数。

以各单元形状为球面的微透镜阵列为例，刀尖圆弧半径补偿如图3所示。假设微透镜阵列的球面单元的球半径为RQ，单元深度为hQ，刀尖圆弧半径为R。以微透镜阵列的基面为参考面（基面处h=0），进行Z轴方向的刀尖半径补偿后，微透镜阵列表面上任意点P对应的刀心位置表示为PT（θ（tP），r（tP），hT（tP）），可由式（3）计算刀路轨迹（图4）。

2 振动对切削轨迹的影响

在超精密加工中，刀尖与工件存在着小幅值的低频振动，是影响加工形貌和粗糙度的重要因素。刀尖与工件之间的振动是由机床振动、主轴跳动等因素综合影响的结果，可以分解到机床的XYZ三个方向上，而每个方向的振动分量可近似为简谐振动[6]，如式（4）所示，其中ax，ay，az分别表示3个振动分量的振幅，fx，fy，fz表示振动的频率，φx，φy，φz表示振动的初始相位，为了便于计算说明，本文假定初始相位均为0。

XYZ方向的振动不仅会造成实际切削点的偏移，也会改变切削深度，最终影响工件表面的形貌和粗糙度。不少学者对振动的影响进行了影响[6-7，10]，然而其研究并没有综合分析3个方向的振动分量对阵列表面影响。

图5描述了XY方向振动分量对切削轨迹（在XY平面的投影）的影响。在极坐标系中，X方向的振动改变了轨迹上的点的极半径值，在振动影响下，理想的轨迹点A偏移到了A'处;而Y方向的振动造成轨迹上点的极角度和极半径的变化，在主轴旋转了θ角度后，刀心位置/应该由B点转移到C点，但振动的影响改变了C点的位置，实际的刀心点偏置到了C'。而Z方向的振动分量则影响刀尖与工件的距离，使得实际切削深度发生变化。振动导致的偏移量可用式（5）表示。

振动因素导致了切削轨迹的偏移，在加工微透镜阵列过程中，实际轨迹表达式为式（6）。为求解实际的轨迹坐标点（θi（ti），ri（ti），hTi（ti）），在极坐标下按照等角度间隔Δθ做轨迹离散化，联合式（6）求解每个角度截面上的轨迹点对应的时间ti序列，进而求解出ti序列的轨迹坐标值。

以2×2的球面单元微透镜阵列为例，考虑了刀具半径补偿（假设刀尖半径R=0.5mm）及振动因素后的切削轨迹如图6所示，为了更好体现振动的影响，图中仿真的加工每转进给量、振动幅值均作了放大处理。

3 表面形貌生成

超精密车削的表面轮廓可以看作是刀具轮廓以进间隔连续运动扫掠而成[6]，工件上每个径向截面的轮廓是由刀刃轮廓交点以及最小轮廓边组成，根据刀心的位置可计算出工件表面各个点的残留高度值图3。使用同样的切削参数，即每转进给量f不变，在加工不同球半径（曲率）的透镜得到的残留高度hc是不相同的，这在后续的仿真实验中进行了验证。

为计算残留高度值，如图7所示，对工件表面按照等角度间隔Δθ划分径向截面，每个截面沿径向按照等间距Δr划分，形成网格并计算各个网格节点的坐标值。截面上的轮廓由该截面上加工轨迹点的位置决定，各节点的残留高度值 hSPcut可按照下式计算。

基于工件表面网格节点的坐标数据，可以拟合仿真出加工表面的形貌，按照式（8），可以计算出工件表面的粗糙度值Ra，其中NS表示表面离散网格节点的总数。

4 仿真分析

本文使用Matlab软件进行模型仿真，图8为微透镜阵列的仿真加工表面形貌，仿真参数见表1。

在建立了仿真模型后，本文研究了透镜尺寸、切削参数对加工结果的影响，使用模型计算了不同参数下的仿真预测结果见图9～10，仿真中除了对比的仿真参数取不同数值外，其它参数均与表1数据相同。

如图9所示，在一定范围内，随着透镜球半径的增大，微透镜单元的平均粗糙度值逐渐减小。这是由于在主轴转速和进给量都保持不变时，加工的每转进给量f恒定，根据本文提出的刀具圆弧半径补偿方法可知，当透镜单元的球半径增大，同一径向界面上相邻刀心在工件半径方向的距离不变，而在Z方向上的距离减小，从而使得加工表面的残留高度

hc和粗糙度Ra都减少。但从图9数据可见，当透镜单元球半径增大到15mm后，球半径对粗糙度的影响已经很小。图10数据说明了当主轴转速恒定，随着进给速度提高（每转进给量增大），透镜单元的平均粗糙度也逐渐增大。且针对固定球半径大小的微透镜阵列，随着进给速度的增大，其对粗糙度的影响也增大。

综上分析，在使用慢刀伺服加工球半径值较小的透镜阵列时，设置较小的进给速度值，有利于减少粗糙度。而当进给速度足够小时，继续减少进给速度对提高表面质量所起的效果不大，反而降低了加工效率。使用本文模型，可以在加工前进行仿真分析，选取优选的加工参数。

5 结 论

本文分析了超精密车削加工微透镜阵列的加工轨迹规划方法，研究了加工参数、透镜阵列的几何参数、刀具尺寸，以及刀具与工件之间的振动对微透镜阵列加工形貌和粗糙度的影响，并提出了微透镜阵列表面形貌生成的仿真与粗糙度的预测模型。通过该模型的仿真分析，研究了不同的透镜球半径、加工刀具的进给速度对微透镜单元表面粗糙度的影响。

从仿真结果可见，保持其他参数恒定，子透镜的球半径越大，子透镜的粗糙度越小;而主轴转速恒定，隨着进给速度提高，加工后的粗糙度增大。

参 考 文 献：

[1] LEE Wingbun， KONG Lingbao， CHEUNG Chifai， et al. An Overview of Ultra-precision Diamond Machining of Microstructured Freeform Surfaces[J]. Journal of Mechanical Engineering， 2013， 49（19）： 144.

[2] LI Min， YUAN Julong， WU Zhe， et al. Progress in Ultra-precision Machining Methods of Complex Curved Parts[J]. Journal of Mechanical Engineering， 2015 （5）： 178.

[3] 周京博. 非回转对称微结构表面超精车削轨迹生成及形状误差评价[D]. 哈尔滨：哈尔滨工业大学， 2013.

[4] GUAN Chaoliang， TIE Guipeng， YIN Ziqiang. Fabrication of Array Lens Optical Component by Using of Slow Tool Servo Diamond Turning[J]. Journal of National University of Defense Technology， 2009， 31（4）： 31.

[5] LU X， TRUMPER D L. Spindle Rotary Position Estimation for Fast Tool Servo Trajectory Generation[J]. International Journal of Machine Tools & Manufacture， 2007， 47（9）： 1362.

[6] 李荣彬， 张志辉. 超精密加工的三维表面形貌预测[J]. 中国机械工程， 2000， 11（8）： 845.

LI Rongbin， ZHANG Zhihui. Prediction of 3D Topography in Ultra-preeision Machining[J]. China Mechanical Engineering， 2000， 11（8）： 845.

[7] WANG H， TO S， CHEN C Y， et al. A Theoretical and Experimental Investigation of the Tool-tip Vibration and Its Influence Upon Surface Generation in Single-point Diamond Turning[J]. International Journal of Machine Tools & Manufacture， 2010， 50（3）： 241.

[8] TIAN F， YIN Z， LI S. Theoretical and Experimental Investigation on Modeling of Surface Topography Influenced by the Tool-workpiece Vibration in the Cutting Direction and Feeding Direction in Single-point Diamond Turning[J]. International Journal of Advanced Manufacturing Technology， 2016： 1.

[9] YI A Y， LI L. Design and Fabrication of a Microlens Array by Use of a Slow Tool Servo[J]. Optics Letters， 2005， 30（13）： 1707.

[10]HUANG C Y， LIANG R. Modeling of Surface Topography in Single-point Diamond Turning Machine[J]. Applied Optics， 2015， 54（23）： 6979.

（編辑：王 萍）