数控机床的误差快检与标定研究

李军利

（河源技师学院，广东河源 517000）

0 引言

数控机床是解决精密零件加工的机电一体化设备，具有加工精度高、适用范围广、生产效率高等优点。当前的数控机床在误差检测方面已具有较为成熟的方法，常用的3 类误差检测有基于量尺、基于重力和基于激光的测量方法，其中以激光干涉检测最为常见［1］。FURUTNANI R 等［2］提出用激光干涉仪对三轴机床的20余项指标进行误差检测，并将误差分布运用到其他类型机床。由于激光干涉仪安装复杂，调试程序难度大，且对现场测量环境要求较高，不利于实现机床误差的快速检测［3-4］，本文设计阶梯规结合CCD测微仪的误差检测系统，并消除测量过程中的各项误差，实现了机床误差的快速检测和标定。

1 误差检测系统硬件设计

误差检测系统硬件主要由阶梯规和AuroraII 系列CCD 测微仪组成。其中阶梯规量块由等距离陶瓷块组成，其结构如图1所示。从零点工作面开始，机床按程序依次步进至量块，每次到达量块后，CCD测微仪对其进行测量采样，得到测量面Li（L0，L1，…，Ln）。当机床步进至采样量块时，CCD测微仪测得读数与零点工作面相对位置差值则为机床的误差。

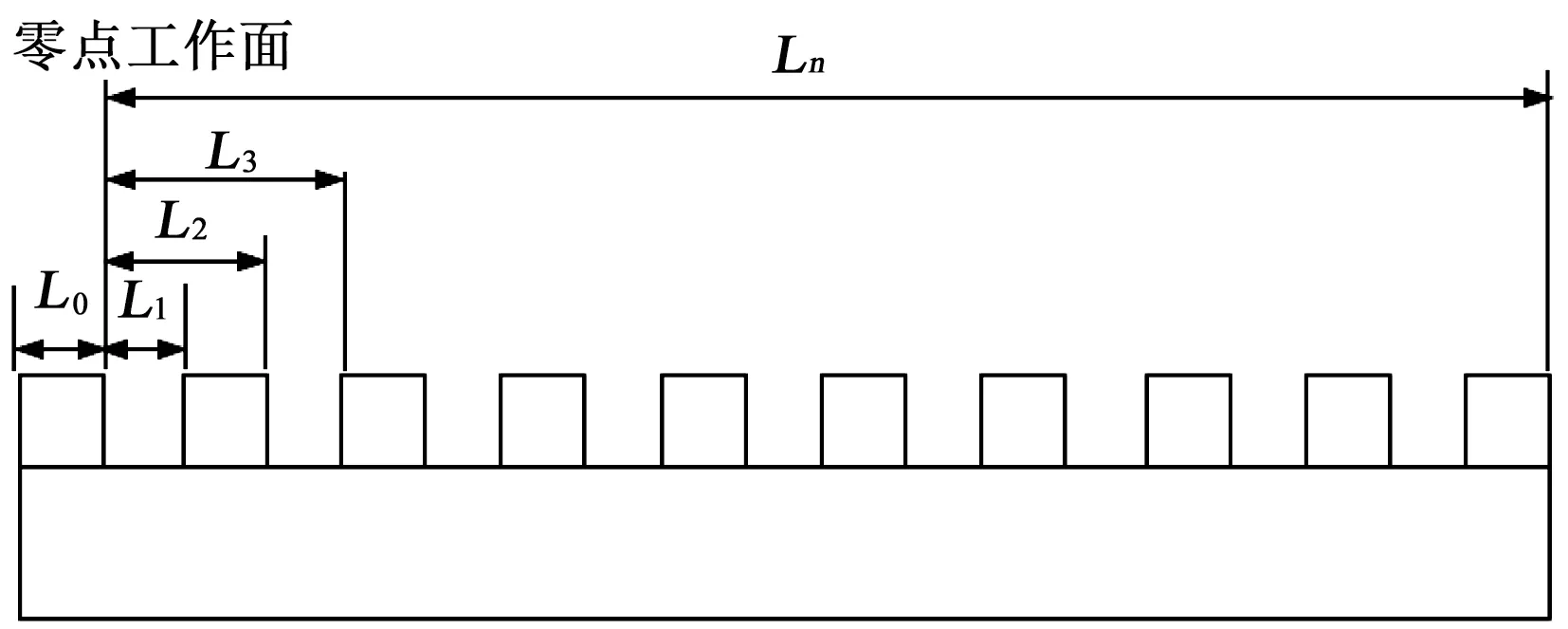
图1 阶梯规工作尺寸图

由于测量仪器在工作状态下不可避免受到一些误差，例如CCD测微仪安装、温度变化、机床工作导致的形变等［5］。针对这些误差，在软件设计时应当考虑在内，并尽量消除随机误差，保持系统误差恒定。一般而言，阶梯规常用的校准温度为22 ℃［6］，螺纹钢的螺距会随温度变化引起一定变化，陶瓷材料的量块则能很好地解决这一问题。在此基础上，阶梯规平均误差减小2%。阶梯规在安装轴线上应当与被检测方向平行，在测量前应当进行校准。为简化操作过程，将两轴之间夹角测量，通过阶梯规可以得出两段的偏移量，进而计算出夹角大小。实际误差与检测值间差值则用夹角表示。

如图2所示，阶梯规空间与测量轴线存在一定误差，其中可以得到以下关系式：

因此，当存在偏移时，机床的轨迹发生移动，其距离为阶梯规量块长度L0/cosθ；检测到的误差ΔL ＝（1/cosθ-1）×L。得到阶梯规不平行待测轴导致的误差，最大偏差为0.95 μm，最小偏差为0.2 μm，这样就能消除阶梯规与测量轴线不平行导致的误差。

2 误差检测系统软件设计

整个系统软件主要是将CCD测微仪测得的数据通过数模转换后输入计算机，并通过误差检测算法对误差进行消除。图3所示为误差检测系统的软件流程。

图2 阶梯规的空间位置

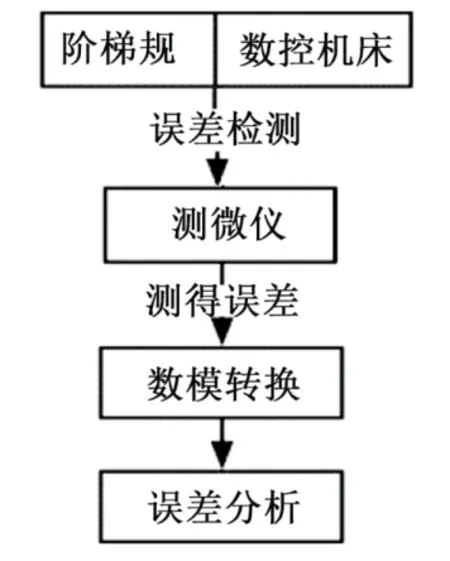
图3 误差检测系统软件流程

当机床开始步进，CCD测微仪将机床与阶梯规测得误差记录，并通过数模转换输入误差检测模型中进行误差分析，并根据数据生成相应的曲线图，测量完成时可以得到数控机床的标定文件，并按照文件进行调整。为了更好地实现误差快检，本文将支持向量机的误差算法模型引入，通过历史误差数据输入支持向量机模型，得到当前误差，实现误差检测系统的标定［7］。常用的支持向量机误差算法具有可约束、精度高等特点，可以将误差转换为线性方程组进行求解，大大提高了误差的计算速度，算法模型见参考文献［8］。

首先将一组测得误差值视为一组由确定误差系统产生的组合，将误差测量时间t、测得误差E（t）建立关系，由下式表示：

当前测得误差可由历史误差计算得到。式中：n为历史误差的维度。维度的选择应由实际误差大小决定，通过实验得到当维度大于5时，预测的误差已能控制在有效范围内，因此维度设定为5。将机床作业时测量得到的误差数据看作以时间为序列的一组离散值，在作业完成时可以将误差作为样本输入支持向量机模型，这样就能得到一组关于时间t 的预测值，可以做到短期内预测。由于维度选择5，维度大于5的预测值已经不再发生变化，此时认为在充足误差数据源输入后得到最准确的预测值。

3 误差测量与标定分析

本次实验采用的数控机床行程为210 mm×450 mm，设计的阶梯规L0、L1均为45 mm，共10 节，标定时温度控制在22～24 ℃，测微仪误差小于0.3%。当机床按照既定程序步进，每至一个测点暂停4 s。同时，将第一组测量结果作为支持向量机输入，并得出当前机床误差。

3.1 不同材质阶梯规误差测量分析

将陶瓷、钢两种材料同种规格阶梯规作为量具同时进行误差测量，在数控机床步进时记录机床测点与阶梯规量块偏差，严格按照机床误差测量方法进行。

图4～5 分别为两方向测得不同材质阶梯规下的机床误差。采用钢材质阶梯规测量的机床正向平均位置偏差最大为91 μm，最小为68 μm；陶瓷材质最大为72 μm，最小为56 μm；垂直方向的钢材质阶梯规测得最大位置偏差为32 μm，最小为22 μm，陶瓷材质最大为30 μm，最小为18 μm。在步进过程中，陶瓷材质阶梯规测得误差趋于平稳，说明在机床环境变化导致钢材质阶梯规自身出现误差，平均约2%，因此用陶瓷材料可以避免因环境温度等因素的变化引起的量具自身误差。

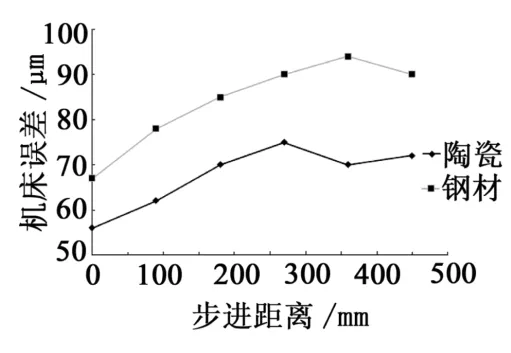
图4 不同材质阶梯规测水平方向误差曲线

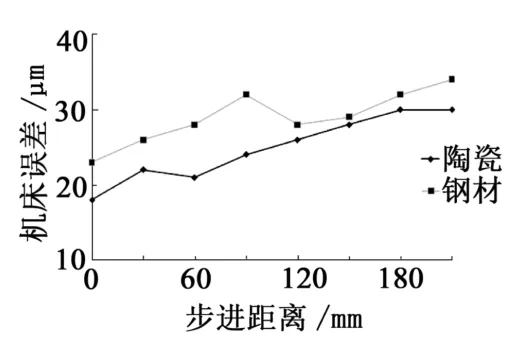
图5 不同材质阶梯规测得垂直方向误差曲线

按照陶瓷阶梯规测量的第一组数据对机床进行标定，标定后再次对机床进行一组步进测量，得到的结果如表1 所示。机床误差结果说明数控机床标定后误差得到减弱，此类误差是由空间误差、动态误差等引起。在机床标定前，测得机床的平均定位精度为48.3 μm，而标定后定位精度减为39.7 μm，此类误差占总误差的17%，由环境温度引起的误差减小2%。

表1 机床误差结果 μm

3.2 不同步进速度结果分析

为了避免步进速度对实验结果造成的误差影响，需对不同步进速度造成的误差结果进行分析，以确认误差影响范围。实验采用3种步进速度，并按同样的方法对机床进行误差测量，其结果如表2 所示。根据测量结果可知，不同步进速度对误差检测的影响较小，最大平均定位误差不超过5.6 μm，反向间隙不超过1.9 μm。按照上述测量结果和温度造成的误差比对，发现由步进速度造成的热误差能在可控范围内，所以机床的步进速度在一定程度上不会对测量结果产生较大影响，可当作随机噪声平滑处理。

表2 3 种步进速度的误差结果

3.3 综合标定结果分析

采用本设计误差快检系统结合支持向量机模型，可以快速判断快检系统的阶梯规、CCD 测微仪在工作一段时间后是否需要进行标定。让快检系统配合机床运行完整步进，同时用支持向量机计算当前误差，然后开始标定。表3 所示为5组机床步进快检系统测量结果。快检系统在前4 组测量中，因自身引起的误差在逐渐减小，但超过4 组后，支持向量机模型计算得出结果小于平均定位精度16%，此时应对测量系统重新进行标定，再次步进测量后，如果平均定位精度和支持向量机算得结果较吻合，则可再次进行测量。

表3 机床误差结果 μm

4 结束语

本文以阶梯规为核心，结合高精度CCD测微仪实现机床快速误差检测，在保证阶梯规与机床姿态稳固的情况下，改进操作步骤，结合激光干涉仪进行标定实验。试验结果证明，本设计能在小于4组的测量中保证快检系统与待检机床的位置精度，减少温度等环境因素引起的误差，结合支持向量机算法模型能快速完成装置本身的标定，实现安装、部署、测量及标定的快速可靠性。