一种改进的花朵授粉优化算法*
2020-08-26解成能刑继刚
陈 强,解成能,刑继刚,赵 航
(长春工业大学机械工程系,长春 130012)
0 引言
传统的优化求解方法有共轭梯度法[1]、动态规划法[2]、牛顿法、Powell方法等数值计算方法。近年来,一些新兴元启发式算法不断涌现,如通过蚂蚁找寻食物的行为受到启发提出的蚁群算法(ACO)[3];由萤火虫特殊求偶方式受到启发得到的萤火虫算法(FA,GSO)[4];通过大自然降雨过程模拟的水循环算法(WCA)等。英国的Yang[5]在2012 年根据花朵授粉过程提出花朵授粉优化算法(Flower Pollination Algorithm,FPA),并成功应用到函数问题优化中。通过不断地应用,该算法表现出显著的寻优性能。由于花朵授粉算法具有一系列优点,使得该算法在被提出之后引起了很多关注,成为了目前智能优化领域的热点研究算法之一。2015 年,Zhou Yongquan等[6]提出了一种基于精英对立的花朵授粉算法(EOFPA),提高了开发和探索能力。2016 年,Zhang Mingxin[7]提出了一种基于混沌理论(IFPCH)的花朵授粉算法求解定积分的新方法。2017 年,Dao Thi-Kien 等[8]提出了一种新的紧凑型花朵授粉算法,用于求解受限硬件条件下的一类优化问题。2018年,Zhang Xinming等[9]将小生境策略与花朵授粉算法相结合,提出了一种新的小生境花朵授粉算法。2019年,Chen Yang等[10]采用混沌映射方法对算法探索阶段的方程进行了改进,提出了一种改进的全局花朵授粉算法(GFPA),用于混沌和超混沌系统的参数辨识。花朵授粉算法虽然具有鲁棒性强、参数少、结构简单、稳定性和执行效率高等诸多优点,但也存在一定的缺点,例如该算法中涉及参数少、缺少一定的理论基础、执行到后期时算法收敛速度明显变慢、在执行过程中容易陷入局部最优无法自动跳出、整体收敛性的相关理论证明不够充分等。所以,花朵授粉算法在充实完善相关理论和拓展应用范围等方面还有待研究。本文提出将线性权重和优质解随机游走策略融入到花朵授粉算法中,以提高花朵授粉算法的性能。
1 花朵授粉算法
1.1 基本概念
自然界开花植物的授粉过程大概分为自花授粉和异花授粉两大类。自花授粉是指基于风媒、水媒授粉的植物;异花授粉是指基于虫媒、鸟媒授粉的植物。同一植物个体上的不同花朵之间的授粉是自花授粉;同一植物的不同个体花朵之间的授粉是异花授粉。因为自花授粉在同一植物个体的不同花朵之间传粉,花粉的移动范围较小,抽象到花朵授粉算法中,就是搜索范围较小的局部搜索;异花授粉需要虫媒或者鸟媒来携带花粉进行授粉,而这些虫类或者传粉者通常采用Levy飞行机制移动[5],Levy飞行是一种特殊的随机游走,因为其能够进行较大步长的移动,所以异花授粉抽象到花朵授粉算法中,即为搜索较大的全局搜索。
在现实中,大部分植物都开许多花,每朵花包含上万个花粉。为了简化研究,假设每株植物只有一朵花,每朵花只产生一个花粉,每个花粉对应优化问题的一个解。根据以上原理,将花朵授粉过程抽象为以下模型:
(1)把生物授粉和异花授粉看作全局授粉过程,并且传粉者的移动路径遵循Levy飞行;
(2)自花授粉视为局部授粉;
(3)花粉的恒常性被看作花朵的繁衍概率,这个概率体现了花朵之间的相似性;
(4)算法的局部寻优和全局寻优之间的转换由转换概率p控制。
1.2 原理
(1)自花授粉过程
自花授粉是指来自同一开花植物的花粉通过风进行传播花粉的过程,这个过程看作是局部搜索过程。当进行局部搜索时,花粉的位置公式(1)更新:

(2)异花授粉过程
异花授粉过程中,传粉者遵从Levy飞行规律,飞行相对较远的路程进行授粉。花粉的位置公式(2)更新:

昆虫在携带花粉时可以用不同的运动方式移动一大段距离,其移动的步长符合Levy 分布。L(λ)>0,其表达式如下:

式中:Γ(λ)为标准的伽马函数。
2 改进花朵授粉算法
2.1 线性权重
本文提出应用线性权重来逐步提高算法的局部搜索能力,即:

式中:wmax为最大权重;wmin为最小权重;itermax为最大迭代次数;iter为当前迭代次数。
异花授粉过程中,花粉的位置公式更改为:

2.2 优质解随机游走策略
本文提出一种优质解随机游走策略,进一步提高算法的搜索能力。

式中:xbest、xsbest、xtbest分别为当前迭代排在前三位的最优解;c1、c2、c3为随机游走参数。
2.3 改进的花朵授粉算法流程
Step 1:设置种群规模N,维数d,最大迭代次数itermax,转换概率p。
Step 2:计算适应度值xi,并得到g*。
Step 3:若rand <p,则按照式(3)、式(5)更新。
Step 4:若rand ≥p,则按照式(1)更新。
Step 5:执行优质解随机游走策略。
Step 6:判断是否满足需要,满足则结束;不满足则返回步骤3。
改进的花朵授粉算法的伪代码如下所示。
输入:种群规模N,维数d,最大迭代次数itermax,转换概率p等参数。
输出:最优解。
算法描述:
(1)产生初始种群
(2)计算适应度值xi,并得到g*
(3)while (t < itermax)
(4)计算权重
(5)fori=1∶N
(6)if 若rand < p,则按照式(3)、式(5)更新
(7)else 依据式(1)局部搜索
(8)end if
end for
(9)if f(xnew)< f(g*),则替换当前最优位置g*为xnew否则放弃
(10)执行优质解随机游走策略
end while
3 实验数据及分析
为验证改进花朵授粉算法的性能,选择5 个测试函数进行对比试验[11],并与遗传算法[12]、引力粒子群算法[13]和基本的花朵授粉算法[5]进行比较。具体测试函数如下。
(1)Sphere函数

该函数在(0,…,0)处取得最小值0。
(2)Schwefel2.22函数
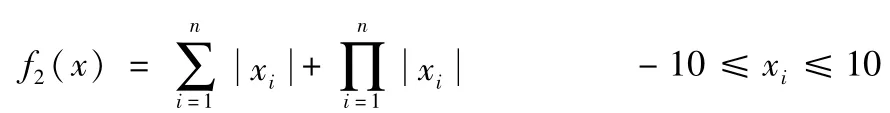
该函数在(0,…,0)处取得最小值0。
(3)Schwefel1.2函数

该函数在(0,…,0)处取得最小值0。
(4)Schwefel2.21函数
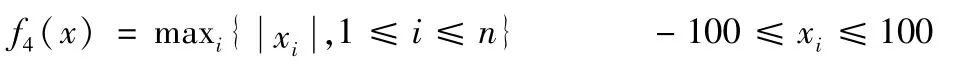
该函数在(0,…,0)处取得最小值0。
(5)Rosenbrock函数

该函数在(1,…,1)处取得最小值0。
以上优化函数,维度为30,每个算法独立运行30次。算法参数:种群规模n =20;转移概率p =0.8;最大迭代次数itermax=300。5个函数的结果对比分别如表1~5所示。

表1 在Sphere函数上优化结果对比

表2 在Schwefel2.22 函数上优化结果对比

表3 在Schwefel1.2 函数上优化结果对比

表4 在Schwefel2.21 函数上优化结果对比
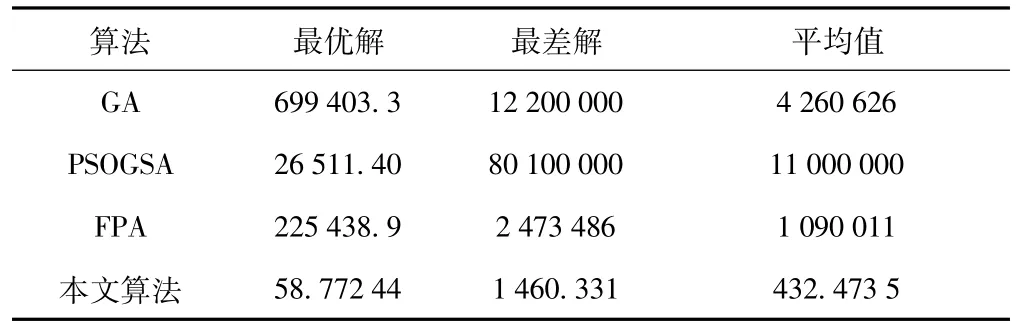
表5 在Rosenbrock函数上优化结果对比
算法收敛的速度是算法性能的重要指标。不同函数的收敛曲线图分别如图1~5所示。

图1 Sphere函数收敛曲线

图2 Schwefel2.22 函数收敛曲线

图3 Schwefel1.2 函数收敛曲

图4 Schwefel2.21 函数收敛曲线

图5 Rosenbrock函数收敛曲线
由表1~5和图1~5可以看出,本文提出的改进FPA算法比基本FPA算法在全局寻优方面具有更快的收敛速度和更高的精度,可以提高算法找到全局最优解的概率。
4 结束语
本文采用线性权重和优质解随机游走策略,改进花朵授粉算法。将该改进型花朵授粉算法用于Sphere 函数、Schwefel2.22 函数、Schwefel1.2 函数、Schwefel2.21 函数、Rosenbrock函数。仿真实验结果表明,所提出的算法在收敛精度和收敛速度方面有明显优势。
