基于电润湿效应驱动的微泵设计与分析
2020-08-26温锦锋陈美蓉
温锦锋,江 帆,沈 健,祝 韬,陈美蓉
(广州大学 机械与电气工程学院机电工程系,广东 广州 510006)
引言
微流体系统广泛地应用于化学分析、生物防御、分析生物学以及微机电系统(MEMS)等方面[1]。而在许多的微流体系统中,微泵是一个重要的组成部分。
传统的微泵按照工作原理一般分为机械式微泵和非机械式微泵[2-3]。但是传统的机械式微泵一般结构复杂,制作成本高,而传统非机械式微泵一般需要在外部增加复杂的驱动电路或设备。为了克服传统微泵的不足提出了一种基于EWOD现象驱动的微泵。
介质上电润湿效应(EWOD)是一种通过施加电压来改变液滴接触角大小的方法,如图1所示。通过改变液滴某一侧与固相的接触角,进而在液滴的表面可以产生压力梯度,从而可以驱动液滴。在许多的研究中都证明利用EWOD现象驱动液滴是一种可行的方案[4-6]。2011年,SHABANI等[7]提出了一种利用EWOD现象驱动液滴直线运动的微泵。但是还存在一些缺点,例如:
(1) 这种结构的微泵本质上还是离散液滴的移动,并不是连续液体的泵送;
(2) 该微泵的泵送会消耗液滴,所以该微泵若要持续工作需及时人为补充液滴。

图1 EWOD原理图
而本研究提出了一种基于EWOD现象驱动的微泵,如图2所示,该微泵通过EWOD现象控液滴在泵腔内往复周期性的振动,进而实现泵腔内容积周期性变化,再加上锥形流阻单向结构的作用[8-9],从而可以在没有任何机械运动结构的情况下实现连续流体的持续运输。

图2 EWOD微泵原理示意图
1 电浸润驱动的原理
1990年MATSUMOTO等[10]就对通过电控制液体之间表面张力的公式进行推导,但是其推导过程中并未明确说明忽略重力的影响以及并未考虑介电层的影响。
为了衡量表面张力与重力大小之间的关系需要计算邦德数Bd:
式中, Δρ为相接触液体的密度差;g为微重力加速度;r为液体所在的容腔内的当量半径;σ为液体的表面张力。在微流体系统中r的尺寸非常的小,因此邦德数非常的小,所以在下面的公式中可以忽略重力的影响。
液体表面的改变与单位表面能量的变化有关,在这里定义单位表面能量的大小为γ。其中液-液-固三相的接触角是由接触点的力平衡所决定的,如图3所示。其中初始平衡时的接触角θ0,可根据杨氏方程给出:
γsl1+σl1l2cosθ0=γsl2
(1)
式中,γsl1为液滴与固相之间的初始单位表面能量;γsl2为外围液体与固相之间的初始单位表面能量,图3中液滴为液体1,包裹液滴的外围流体为液体2;σl1l2为液体1与液体2之间的表面张力。
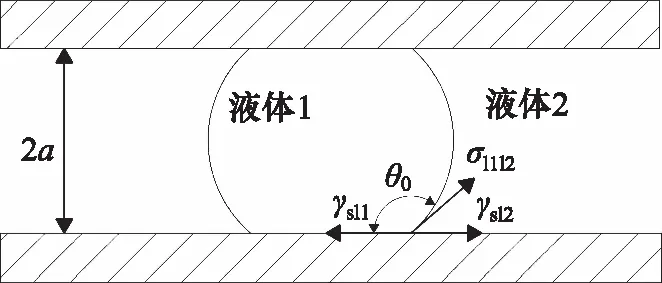
图3 初始时刻γsl1,γsl2以及σl1l2平衡时的示意图
根据亥姆霍兹模型,在EWOD现象中可以将介电层看成是双层平行板电容,因此电容可根据下面公式进行计算:
(2)
式中,CH为亥姆霍兹模型中介电层的电容;ε0为绝对介电常数;εl为液滴的相对介电常数;A为介电层的面积;δ为介电层的厚度。
根据电容的能量公式:
(3)
式中,U为电容的能量;V为电容的电压。
根据式(2)和式(3)可推导出:
(4)
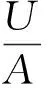
根据式(1)和式(4)可推导出:
(5)
式中,θew为发生EWOD现象后液滴与固相的接触角,见图1。
根据式(1)和式(5)即可得发生EWOD现象之后的接触角公式:
(6)
根据拉普拉斯方程有:
(7)
式中, Δp为液滴与外围液体两相界面产生的初始压强差;R1,R2为在三维空间中液滴的曲率半径。
在没有发生EWOD现象的一端,根据式(2)和式(7),在二维平面上有:
(8)
在发生EWOD现象的一端,根据式(5)和式(7),在二维平面上有:
式中, Δpew为发生EWOD现象之后液滴与外围液体两相界面的压强差;a为泵腔的高度的一半。
所以在液滴没有发生EWOD现象一端与发生EWOD现象一端之间就会产生一个压力差ΔpEW:
(10)
根据式(10),因为产生了压力差ΔpEW从而液滴可以运动。所以当周期性的转换液滴所触碰的2个电极的正负极性时即可实现液滴的振动。
2 电浸润微泵的设计
2.1 微泵的几何模型
为了初步验证提出的微泵是可行的,EWOD微泵的模型尺寸,如图4所示,数值模拟的边界条件参考了2002年POLLACK等[11]做的实验以及2006年MOHSENI等[12]做的仿真。在泵腔中负责振动的液滴直径为1900 μm;泵腔为300 μm×1500 μm×5000 μm的长方体腔体;泵腔中贴有边长为1500 μm的正方形电极,并在正方形电极上涂有60 nm厚的Teflon介电材料,其介电常数为2.2;锥形流阻单向结构的锥角为9.15°;电线用于连接外部电源正负极;当周期性的转换液滴所触碰的2个电极的正负极性时即可实现液滴的振动;在未施加电压时液滴的初始角度为104°;其中当施加电压时对应的接触角如表1所示。

表1 施加的电压对应的接触角

1、2.正方形电极 3.液滴图4 EWOD微泵结构图
2.2 控制方程
为了缩短计算时间和节省计算资源对本模型做出如下假设及简化: ① 假设微泵的工作是在二维平面上的; ② 基于EWOD现象导致的液滴接触角的变化由式(6)给出; ③ 流体是不可压缩的; ④ 流体的运动符合层流; ⑤ 流体为牛顿流体; ⑥ 在微尺寸下影响微流体运动的主导作用力不再是重力更多的是表面张力以及摩擦力,因此可以忽略重力的作用; ⑦ 因为电极板和介电层的厚度通常都是纳米级别的,因此忽略电极板和介电层的体积。
利用COMSOL Multiphysics中的两相流-相场模型对本模型进行数值模拟。
其中全局控制方程[13]为质量守恒方程:
ρV·u=0
(11)
动量守恒方程:
K=μ(▽u+(▽u)T)
(12)
式中,ρ为流体的密度;u为速度矢量;μ为流体的动力黏度;t为时间;p为流体的压力;g为重力加速度;σl1l2为表面张力,其中表面张力σl1l2在仅界面处定义为非零;E为单位矩阵。
2.3 模型校准
在数值模拟分析中,振动的液滴为0.1 mol/L的KCl溶液,被运输的微流体为配比好的硅油,其基本物理属性如表2所示。

表2 材料的基本物理属性
图5展示了单个直径为1900 μm液滴在0.005 s内分别在电压40, 44, 48 V作用下在300 μm高的流道内运动的情况;图6展示了单个直径为1900 μm液滴在0.005 s内分别在电压40, 44, 48 V作用下在微泵泵腔内运动的情况。

1.水滴 2.硅油图5 液滴在流道内的运动图
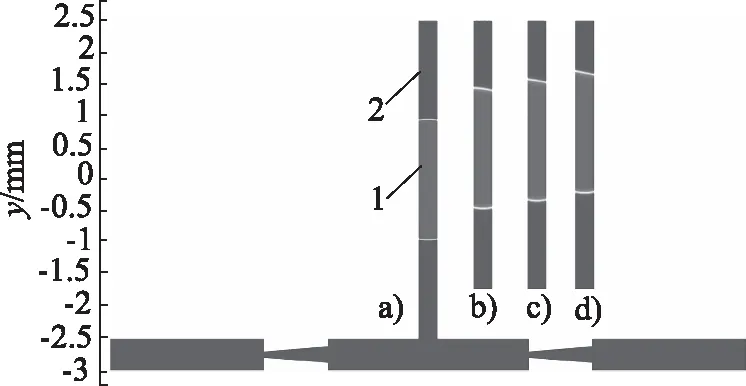
1.水滴 2.硅油图6 液滴在泵腔内的运动图
图7展示了接触角分别为80°,82°,84°,86°和88°时在300 μm高的流道内的速度图,以及接触角分别为80°,82°,84°,86°和88°时在微泵泵腔内的速度图。
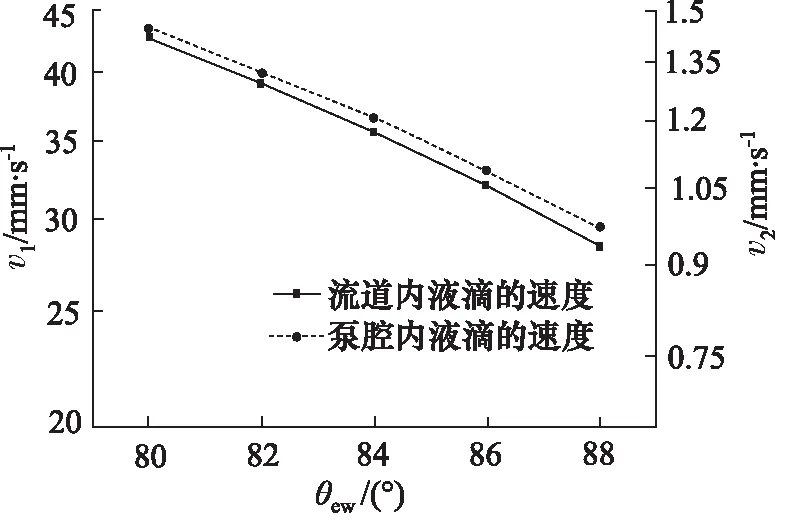
图7 液滴速度曲线图
仿真的结果与2002年POLLACK等[11]做的实验和2006年MOHSENI等[12]做的仿真数据相符。
2.4 网格敏感性的验证
在COMSOL Multiphysics中网格的密度主要由最大网格单元尺寸决定,因此可以通过改变最大网格单元尺寸来改变网格密度,进而评判网格的敏感性。如图8所示表示在EWOD微泵中最大网格单元分别为0.379, 0.369, 0.359, 0.349 mm时对应的EWOD微泵中液滴运动的曲线最大单元尺寸0.369 mm所对应的速度图与图7泵腔内液滴的速度图是一致的。

图8 不同最大网格单元尺寸对应的速度图
从图8可以看出随着最大网格单元的减小EWOD微泵内液滴的移动速度也有相应的变化,其中最大网格单元网格尺寸从0.379 mm变成0.369 mm时,泵腔内液滴移动的速度最明显,但是当最大单元网格尺寸变为0.359 mm以及0.349 mm时泵腔内液滴的速度变化并不明显。因此在保证计算精度的前提下,从节约计算资源的角度出发,在划分网格时选取的最大网格单元尺寸为0.369 mm。
3 结果分析
图9展示了发生EWOD现象接触角为80°,振动频率为10 Hz时,一个周期内的EWOD微泵内部流域的运动情况。
图10展示了发生EWOD现象时接触角为80°时,4种振动频率分别为5, 10, 15, 20 Hz的液滴所对应的微泵出口在0~5 s的流量图。从图中可以明显的看出,在微观上流量是有上下脉动的,但是由于锥形单向流阻结构的作用,在微泵出口处流出的液体比流入的液体更多,所以在宏观上可以形成单向流动。而且从图上可以明显看出在微观上随着液滴的振动频率增加所对应的流量图上下波动的范围减小,所以提高液滴的振动频率可以使微泵的输出更加平缓。
其中,在第5 s时振动频率分别为5, 10, 15, 20 Hz 的液滴所对应的流量大小分别为:4.67×10-3,7.34×10-3,8.18×10-3,8.43×10-3mm3,可见微泵的泵送效率和液滴的振动频率有关。
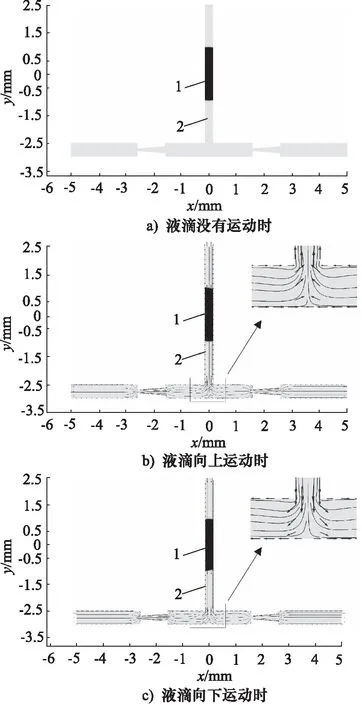
1.水滴 2.硅油图9 EWOD微泵内部流域图

图10 EWOD微泵出口流量图
图11展示了发生EWOD现象时接触角为80°时,4种振动频率分别为5, 10, 15, 20 Hz的液滴所对应的的微泵出口在0~5 s的平均压力图。从图中可以看出EWOD微泵出口的压力是随着液滴的振动而波动的。
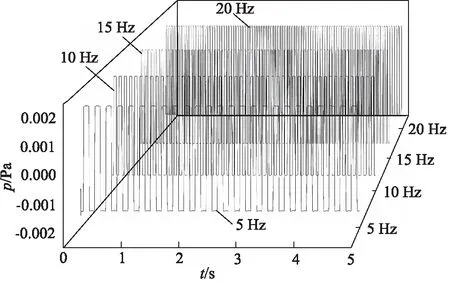
图11 EWOD微泵出口压力图
其中在0~5 s内,频率为5, 10, 15, 20 Hz时对应的最大压力均为1.90×10-10MPa,最小压力均为-1.88×10-10MPa。可见微泵出口的压力与液滴的振动并没有太密切的联系。
4 结论
(1) 本研究的电浸润微泵提供了一种微泵全新的驱动方式,为微流控系统驱动元件的设计指明了一个新方向;
(2) 通过对电浸润微泵的进行数值分析,揭示了在工作状态中微泵内部流域的情况,当液滴向上运动时微流道的液体被吸入泵腔,当液滴向下运动时泵腔内的流体被推进微流道;
(3) 数值分析结果表明当为80°时,微泵的流量随着振动频率的增加而增加,而且流量的波动随着振动频率的增加而减小。所以提高振动频率可以增加微泵的流量和减缓流量的波动;
(4) 数值分析结果表明当为80°时,微泵出口处的压力并没有随振动频率的增加而发生变化;
(5) 对于电浸润微泵的研究目前还处于理论阶段,后续的研究应多从实验着手获取更准确的数据。
