多层螺旋线圈电磁超声换能器优化设计及其实验研究
2020-08-26唐琴石文泽卢超陈巍巍张金陈尧黄祺凯程进杰
唐琴,石文泽,2,卢超,3,陈巍巍,张金,陈尧,黄祺凯,程进杰
(1.南昌航空大学无损检测教育部重点实验室,江西南昌,330063;2.中科院声学研究所声场声信息国家重点实验室,北京,100190;3.上饶师范学院大数据分析与云检测重点实验室,江西上饶,334001;4.中国人民解放军陆军炮兵防空兵学院,安徽合肥,230031)
电磁超声换能器(electromagnetic acoustic transducers,EMATs)在金属材料中通过电磁耦合方式激励和接收超声波。与传统的超声检测相比,电磁超声检测技术无需耦合剂,对待测试样表面粗糙度和检测环境要求不高;同时,通过改变永磁体的偏置磁场和线圈的组合方式可激励出不同模式的超声波[1-3],改变激励信号的频率即可改变超声波的传播方向[4]。综合上述优点,电磁超声检测技术已经广泛应用于石油管道检测[5-6]、钢轨踏面裂纹检测[7-8]和高温环境下在线检测[9]。然而,EMAT的低换能效率和易受检测环境噪声干扰等问题限制了其应用和发展。因此,通过优化EMAT参数以提高换能器的检测效率显得尤为重要。
近年来,国内外学者围绕EMAT 的优化设计进行了广泛研究。 在有限元建模方面,KALTENBACHER 等[10]通过有限元数值模拟方法,建立了EMAT 超声波激励和接收过程,并进行了实验验证。但模型中假定永磁体磁场均匀分布,没有考虑导体材料的集肤效应和邻近效应,不能准确反映EMAT设计参数对换能效率的影响规律。WANG 等[11]采用数值法与解析法相结合,建立了一种改进的3-D 曲折线圈表面波有限元模型,重点研究动态磁场作用下表面波的声场特性和缺陷检测能力,发现当励磁电流超过528.9 A 时,基于动态磁场下的洛仑兹力产生的表面波对裂纹更加敏感。KANG等[12]在此基础上进行了拓展研究,通过正交实验设计方法,获得了EMAT 最佳参数组合,发现永磁体的宽度为线圈宽度的1.22 倍、长度与线圈相同时,表面波幅值最佳,优化后的EMAT表面波幅值提高了25.2%,且激励电流和导线宽度对动态磁场产生的表面波更加敏感。上述2种有限元模型都是基于动态磁场下的EMAT研究,但在实际检测过程中,动态磁场和静态磁场共同存在,且静态磁场产生的洛仑兹力在检测过程中占主导作用;同时,脉冲功率放大器的输出电流会随着线圈阻抗的变化而变化,很难保证动态磁场产生的超声波对缺陷的检测灵敏度。在EMAT探头优化方面,ISLA 等[13]提出一种新型磁铁布置方式,将多个永磁体轴对称地布置在铁磁芯周围,在试样表面测得磁通密度超过3 T,整个EMAT 探头横波幅值提高了3~6 dB,用线性极化的方式获得了纯度更高的横波信号,但4个永磁体需要对称地固定在铁磁芯周围,加工难度大,对线圈制作要求也较高。JIA 等[14]提出一种双螺旋线圈体波探头,相比于传统体波探头,改进后探头的信噪比增加了5 倍,横波幅值增加了1 倍。何存富等[15]将4个跑道线圈分别进行并联和串联,在小口径管道中激励出低阶扭转模态导波,发现线圈并联激励的回波幅值为串联激励的2倍,但并未涉及EMAT激励等效电路分析串并连接方式和线圈个数对EMAT换能效率的影响。在EMAT硬件电路设计方面,SEHER 等[16]通过变压器模型等效方法获得螺旋线圈EMAT 的终端输出阻抗,发现信噪比与传输灵敏度和接收信号噪声系数的倒数相关。HIRAO 等[17]发现当脉冲功率放大器输出阻抗一定时,通过阻抗匹配电路可以显著提高EMAT 换能效率和激励功率,并给出了阻抗匹配参数、线圈等效阻抗和功率放大器输出阻抗之间的函数关系。综上所述,国内外学者在EMAT 有限元建模和参数优化方面已经取得了较大进展,但是很少关注在恒定电压源的脉冲功率放大器条件下,线圈串并联方式和线圈个数对EMAT 换能效率的影响。在电磁超声激励有限元模型中,通常假设EMAT线圈的激励电流幅值恒定,没有考虑阻抗匹配网络、线圈等效阻抗、传输导线阻抗等综合因素[18]。值得注意的是,激励线圈的等效阻抗与激励频率、被测金属特性、磁场等因素相关[19],由于功率放大器多为恒功率或恒电压器件,当线圈等效阻抗发生变化时,激励电流的幅值和波形均会发生变化。因此,分析脉冲功率放大器在输出电压或者视在功率恒定的条件下,多层线圈阻抗及其参数设计对EMAT 换能效率的影响规律非常必要。为此,本文作者通过建立多层螺旋线圈EMAT 激励过程有限元模型,采用正交试验表,综合分析EMAT设计参数对换能效率的影响,测量多层线圈的等效阻抗,结合EMAT 激励等效电路,对有限元计算结果进行修正,系统地分析多层螺旋线圈串联和并联对EMAT 激励效率的影响,并进行实验验证。
1 EMAT换能机理及控制方程
基于洛仑兹力的螺旋线圈EMAT 换能机理如图1 所示。当螺旋线圈通以高频脉冲激励电流时,试样近表层会产生频率相同、相位相反的感应电涡流Je。感应电流与静态偏置磁场(r 向分量Bsr和z向分量Bsz)和动态交变磁场(Bdr和Bdz)共同作用下产生沿r向和z向的洛仑兹力fr和fz,洛仑兹力带动质点高频振动,产生沿试样厚度方向传播的超声波。
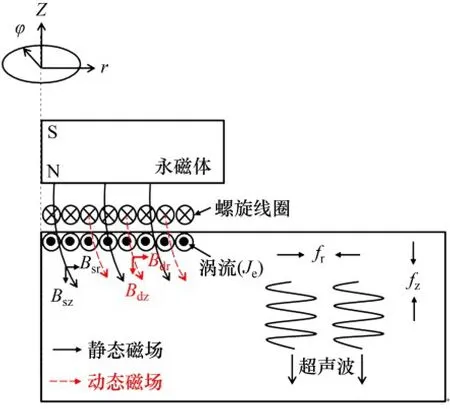
图1 螺旋线圈EMAT换能原理Fig.1 Conversion mechanism of a spiral coil EMAT
1.1 永磁体偏置磁场方程
永磁体提供的偏置磁场是一个无源场,其散度为0,可通过下列方程组表示[20]:

式中:H和φm分别为磁场强度和标量磁位;∇为梯度;B为磁感应强度;Br为永磁体的剩余磁感应强度;μr为永磁体的相对磁导率。
1.2 集肤深度与感应电流
在频率为f的交变电流作用下,集肤深度及螺旋线圈产生的感应电涡流分别为[21]:

式中:δ 为集肤深度;σ 为导体电导率;μ 为磁导率;E为电场强度。
1.3 超声波形成及传播
超声波的形成和传播过程由下列方程给出[22]:

式中:fL为洛仑兹力;Bd为动态磁场;ρ为质量密度;u为位移矢量;T为应力张量。
1.4 EMAT激励端等效电路
考虑功率放大器的恒定电压Uo和输出阻抗Zo以及阻抗匹配电路阻抗和螺旋线圈等效阻抗Zc,EMAT 激励端等效电路如图2 所示[17,23]。通常情况下,假定功率放大器输出阻抗为50 Ω。
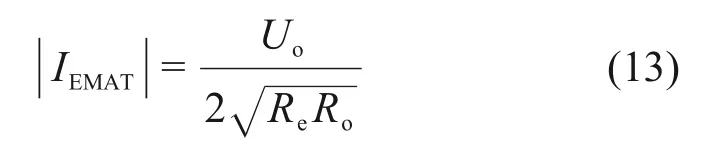
2 EMAT激励过程有限元模型

图2 EMAT激励等效电路Fig.2 Excitation equivalent circuit of EMAT
L 型阻抗匹配网络和线圈阻抗组合以后的阻抗Z1为
式中:Xa和Xb分别为阻抗匹配网路的容抗和感抗,Re为螺旋线圈等效阻抗的实部,Xe为螺旋线圈等效阻抗的虚部。
激励线圈两端的电压VEMAT和功率放大器输出电压U1分别为:

在满足完美阻抗匹配条件下,阻抗网络参数可由下式表示:

其中:

最佳阻抗匹配条件下的螺旋线圈激励电流如下:
多层螺旋线圈EMAT 设计参数如图3 所示,EMAT 主要参数见表1。其中,永磁体剩余磁通量为1.04 T,相对磁导率为1.04,电导率为7.14×105S/m;导线的相对磁导率为1,电导率为6.00×107S/m;铝块的相对磁导率为1,电导率为3.77×107S/m;空气的磁导率为1,电导率为0 S/m。

图3 多层螺旋线圈EMAT几何参数示意图Fig.3 Schematic diagram for geometric parameters of multi-layer spiral coils EMAT

表1 激励EMAT设计参数Table 1 Parameters of excitation EMAT
网格划分和求解器步长影响计算结果的收敛性和准确性。当瞬态求解器时间步长为1/100f(f为激励频率)时,空气域、永磁体、线圈和铝试样的最大网格单位尺寸分别为2,0.3,0.05 和0.3 mm,计算结果基本收敛。由于集肤效应存在[11],线圈、铝块和永磁体的集肤层内的网格不少于7 个,因此,分别在永磁体下表面、线圈导线边界以及铝块上表面设置边界层网格,进行网格细化,得到磁铁下表面、线圈表面以及铝块上表面的第一层厚度l分别为96.3,10.5和13.2 μm。边界层网格参数为

式中:l 为边界层的第一层厚度;m 为边界层的拉伸因子;q为边界层数。
激励EMAT有限元模型网格细化如图4所示。

图4 体波EMAT有限元模型网格划分Fig.4 Meshing grids of finite element model for bulk wave EMAT
通常EMAT 的激励信号为正弦脉冲串调制信号,其表达式为

式中:Io为激励电流;Io= 1 A;ω= 2πf;频率f=1 MHz。
图5(a)所示为永磁体的磁场分布图。由图5(a)可知:沿z 方向的偏置磁场强度大于r 方向的磁场强度,因此r 向洛仑兹力大于z 向洛仑兹力。图5(b)所示为t=10 μs时铝块近表面涡流密度分布。
图6 所示为超声波在铝块中传播的声场快照。由图6可知:对于螺旋线圈EMAT,其激励的超声波主要以横波为主。仿真得到的横波声速为2 933 m/s,与理论波速3 000 m/s 的相对误差为2%,证明模型计算结果可靠。
3 激励EMAT探头优化设计
正交实验设计方法是研究多因素水平的实验方法,利用规格化的正交表选取具有代表性的点进行设计,这些点具有“均衡分配、齐整可比”的特点,能够得到全面的试验分析结果。通过正交实验方法不仅能分析各个参数对换能效率的影响,而且能获取最佳参数组合[22,24]。考虑到EMAT设计参数较多,若按照全面实验,需要进行729次试验,故采用3水平6因子正交试验设计方法分析EMAT参数对换能效率的影响规律,正交实验设计参数及因子水平见表2。

图5 有限元计算结果Fig.5 Simulated results by finite element method

图6 超声波在铝块中的传播过程Fig.6 Ultrasonic waves propagation in an aluminum specimen
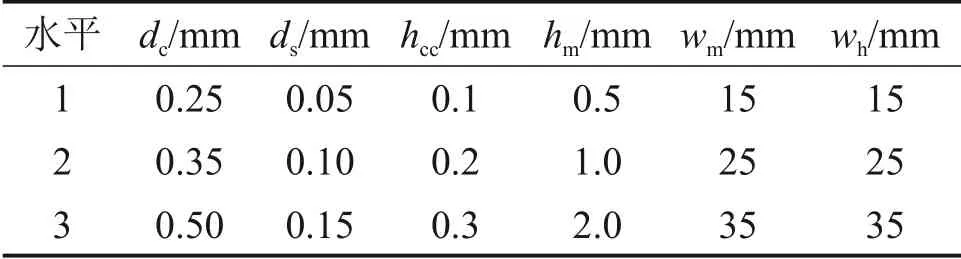
表2 两层线圈激励EMAT设计参数Table 2 Design parameters of two-layer coil of excitation EMAT
EMAT 正交实验组合和仿真结果见表3。横波纯度定义为横波分量与纵波分量比值r/z。螺旋线圈EMAT 在产生横波的同时也会形成纵波,在实际检测中,纵波及其模式转换波的存在可能干扰缺陷定量的可靠性和准确性,甚至可能导致缺陷的误判。因此,横波纯度也是螺旋线圈EMAT 的重要评价指标。
3.1 螺旋线圈EMAT换能效率影响因素分析
根据表3得到激励EMAT设计参数对横波和纵波幅值的影响如图7所示。由图7(a)和(b)可知:随着导线直径dc、导线间距ds增加,横波和纵波幅值明显下降。图7(c)和(d)表明:多层线圈间距离hcc、永磁体与顶层线圈距离hm对横波和纵波基本无影响。图7(e)和(f)表明:随着永磁体宽度wm和高度wh增加,横波纯度也相应增大;当永磁体宽度wm和高度wh均小于25 mm时,横波纯度增幅较缓慢;当wm和wh均大于25 mm 时,横波纯度急剧增大。由图7可知:对于横波而言,影响纯度的各因素从大到小依次为wm,dc,wh,ds,hcc,hm;对于纵波而言,影响纯度的因素从大到小依次为dc,wm,ds,hcc,wh,hm。
3.2 预测最佳实验数据组合
由图7可知:线圈导线直径和永磁体尺寸对体波的幅值影响较显著。取横波幅值最大对应的EMAT设计参数为最优参数组合,dc,ds,hcc,hm,wm和wh分别为0.25,0.05,0.1,0.5,35和35 mm。同理,最差参数组合时,dc,ds,hcc,hm,wm和wh分别为0.5,0.15,0.2,0.5,15和35 mm,根据表3 的正交试验结果,利用Minitab 软件预测出组合EMAT设计参数的横波和纵波幅值,结果如表4所示。由表4可知:最优组合和最差组合条件下,横波预测值与仿真值的相对误差分别为6.01%和4.20%,表明该正交试验预测值与仿真结果基本符合。
在激励EMAT 最佳组合条件下,不同层数螺旋线圈EMAT 对应的横波幅值如表5 所示。由表5可知:与单层线圈相比,2~5层螺旋线圈EMAT对应的横波幅值分别提高了65.0%,126.7%,193.2%和230.4%。横波幅值增幅与线圈层数增加是非线性增长关系,随着线圈层数的增加,永磁体与被测试样距离变大,新增线圈在金属表层形成的电涡流也减小,导致新增线圈在试样表面产生的洛仑兹力变小。因此,随着线圈层数增加,横波的增幅逐渐减小。
4 实验验证
4.1 实验系统组成
电磁超声实验系统框图如图8所示,信号发生器产生1 MHz 的正弦脉冲串,经功率放大器将信号放大,进入激励端阻抗匹配将激励电压加载到发射EMAT 探头上,激励出沿铝块厚度方向传播超声波。接收EMAT 收到感生电压信号,经过接收端阻抗匹配、前置放大及滤波电路,再通过数据采集卡,最终在Labview界面显示出A扫波形。
本文采用一发一收工作方式,激励和接收EMAT探头分别放置于铝试样上端面和下底面。接收EMAT 线圈导线直径为dc=0.20 mm,外径为25 mm,永磁体直径×高度为30 mm×15 mm。
4.2 实验结果及分析
4.2.1 验证最佳参数组合与最差参数组合
图9所示为EMAT的最差参数组合与最优参数组合对应的A扫波形。由图9可知:优化后,横波幅值由0.756 V 增加至1.740 V,横波纯度由2.8 增加到7.9。
4.2.2 多层螺旋线圈EMAT对超声波信号的影响
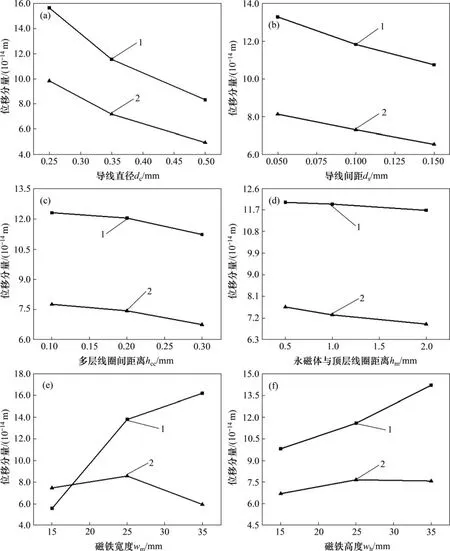
图7 EMAT参数对体波位移的影响Fig.7 Influences of EMAT parameters on bulk wave displacement

表4 预测值与仿真值验证Table 4 Verification of simulated result and predicted value

表5 最佳组合参数时不同层数螺旋线圈对应的横波幅值Table 5 Ultrasonic wave amplitude of different layers spiral coils with optimal combination parameters

图8 电磁超声检测实验系统框图Fig.8 Schematic diagram of EMAT experiment system
采用不同导线直径的螺旋线圈,分别进行多层线圈的串联和并联,作为EMAT 的激励线圈并进行对比实验,并保证每层线圈的电流流向一致,线圈的串联和并联连接方式如图10所示。
采用线径dc分别为0.15, 0.20, 0.25 和0.40 mm的线圈进行多层串、并联对比实验,实验结果如图11 所示。由图11(a)可知:当功率放大器为恒电压源时,随着线圈串联的层数增加,激励EMAT换能效率显著降低,且层数增加越多,下降趋势越明显。图11(b)表明:多层线圈并联时,超声波幅值呈现缓慢下降趋势;随着线圈并联层数增加,新增线圈与试样表面距离增大,导致作用于试样表面涡流密度和偏置磁场均减小,不利于提高EMAT换能效率。
为了分析多层线圈串、并联条件下激励EMAT换能效率降低的原因,采用E4990A阻抗分析仪测量多层线圈串、并联的等效阻抗。表6所示为导线直径dc为0.25 mm、频率为1 MHz时多层螺旋线圈处于无永磁体、无铝块条件下的等效阻抗。由表6可知:对于串联方式,线圈的等效阻抗(实部、虚部)随着线圈层数的增加呈线性增大关系;对于并联方式,n 层线圈的等效阻抗约为单层线圈的1/n。

图9 EMAT的最差参数组合与最优参数组合对应的A扫波形Fig.9 A-scan wave signals from EMAT with optimal combination parameters and worst ones

图10 螺旋线圈连接方式示意图Fig.10 Schematic diagram of connection of spiral coils
当螺旋线圈处于永磁体和铝块之间,频率1 MHz 时等效阻抗见表7。由表7 可知:线圈的阻抗受激励电流频率、被测试样特性等因素影响。当多个线圈串联时,随着线圈层数的增加,等效阻抗迅速增加,增大趋势远远大于无永磁体和铝块条件下等效阻抗的增大趋势;当多个线圈并联时,等效阻抗随层数的增加基本不变。

图11 多层螺旋线圈串并联的横波幅值Fig.11 Amplitudes of shear wave with multi-layer spiral coils connected in series and parallel

表6 直径dc=0.25 mm的多层螺旋线圈在无永磁体和无铝块时的等效阻抗Table 6 Impendence of multi-layer coils(dc=0.25 mm)without a magnet or an aluminum specimen

表7 直径dc=0.25 mm的多层螺旋线圈在永磁体和铝块间的等效阻抗Table 7 Impendence of multi-layer coils(dc=0.25 mm)with a magnet and an aluminum specimen
在满足最佳阻抗匹配参数条件下,5 kW 功率放大器输出电压Uo=707 V,功率放大器输出阻抗Zo=50 Ω。将表7 中多层线圈串、并联阻抗代入激励端等效电路进行分析,得出多层线圈激励电流IEMAT。根据表5中横波幅值进行多层线圈串、并联幅值修正,将实验结果与仿真结果幅值进行归一化比较,结果如图12所示。由图12可知:修正后的仿真结果与实验结果基本一致;多层线圈串联时,线圈等效阻抗增大,激励电流减小,并且随着串联线圈层数增加,永磁体与试样距离变大,导致超声波幅值显著降低;多层线圈并联时,线圈等效阻抗变化较小,单个线圈激励电流降低,新增线圈产生的洛仑兹力减小,导致超声波幅值缓慢下降。
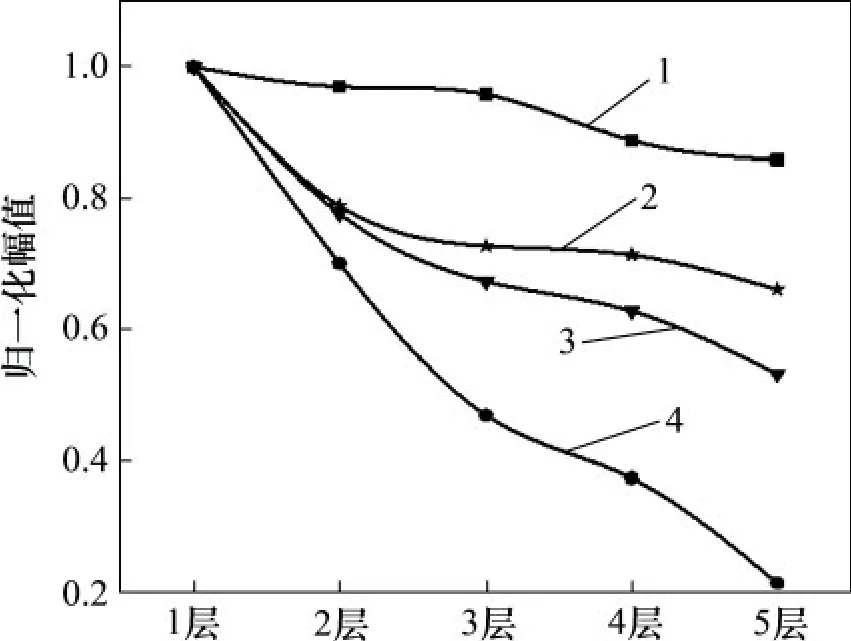
图12 多层线圈串并联仿真和实验的曲线比较Fig.12 Comparison of simulation and experimental results of multi-layer coils connected in series and parallel
5 结论
1) 永磁体宽度和高度、螺旋线圈导线直径、导线中心间距、两层线圈间距对EMAT 换能效率均有影响。对于横波而言,影响最大的因素是磁铁宽度,其次是导线直径和磁铁高度。采用直径更大、高度更高的永磁体能够有效地提高横波纯度。
2)螺旋线圈的等效阻抗与脉冲电流频率、被测试样以及外部磁场有关。在恒电压放大器条件下,多层线圈串联时,EMAT 换能效率显著降低,多层线圈并联时,超声波幅值呈现缓慢下降趋势。
3) 基于恒定电流源的EMAT 有限元模型中,通常假定每层线圈激励电流幅值恒定,增加线圈层数可以提高EMAT 换能效率。但实际中脉冲放大器多为恒功率源或恒电压源,在完美阻抗匹配条件下,多层线圈阻抗变化会导致激励电流的改变。因此,在对EMAT 进行优化设计时,需要考虑线圈的等效阻抗这一因素。
4) 激励EMAT 换能效率与激励等效电路的激励电流相互制约。单方面提高激励电流,就需要减小激励线圈的等效阻抗,但是等效阻抗小的激励EMAT 的换能效率不一定高。因此,有必要采用场路耦合分析方法对激励EMAT 设计参数进行系统性、整体性分析。
