基于BAS-BP模型的装配式建筑投资估算研究

赵维树，王姗姗

(安徽建筑大学经济与管理学院，安徽 合肥 230022)

投资估算作为工程项目投资决策、资金筹措、设计及施工建造等各阶段造价控制的重要依据，贯穿于建设项目全寿命周期，是对项目工程造价影响较大的一个阶段[1]。建设前期投资估算的正确与否，直接关系到整个项目的成败，因此科学、准确且高效的把握估算至关重要。同时由于目前装配式建筑生产的标准化、专业化、规模化程度较低，因而成本高一直是其现阶段发展的一大制约因素，如何控制好装配式建筑项目的投资估算，以避免建造过程中的投资失控问题成为当前该领域研究的重点[2-3]。但由于装配式建筑是一种新型的建造方式，运用传统投资估算方法对其进行估算控制必然是不合理的，必须结合现代智能技术实现快速、精确估算。

研究表明，目前BP神经网络算法、遗传算法、粒子群算法等智能算法被引入工程投资估算领域，能够实现快速估算，较传统估算方法有较明显的优势。其中BP神经网络被广泛应用于建设项目投资估算中，但在装配式建筑领域涉及较少，并且在实际应用中标准BP神经网络容易陷入局部最优，对高复杂线性、非线性混合数据处理收敛速度较慢，预测精度不高[4]。因此本文通过对有效控制投资估算方法的研究，提出基于天牛须搜索算法改进优化的BP神经网络，在此基础上构建估算模型。借助MATLAB软件对模型的仿真测试，最终建立装配式建筑估算模型，为准确预测投资估算提供参考。

1 基于BAS-BP神经网络的估算模型

1.1 BP神经网络原理

BP神经网络(Back Propagation Neural Network，BP)是按照误差反向传播算法训练的一种多层前馈神经网络，其学习规则是运用梯度下降法，通过不断进行误差反向学习来调整网络的权值和阈值，以达到网络误差平方和最小[5]。该算法具有良好的自组织、自适应、非线性映射能力以及高鲁棒性，可以对输入的各类复杂的线性与非线性关系数据进行处理，并能够用于对各类待估测目标进行预测。

通常情况下， BP 神经网络一般设置为三层及以上的网络结构， 由输入层、 隐含层及输出层构成， 网络的学习过程主要包括输入信号的正向传播以及误差的反向传播。 在网络训练时样本数据由输入层进入网络后神经元被激活，其激活值从输入层出发经过中间层向输出层传播，并获得网络的输出结果。然后根据误差信号，从输出层出发再经中间隐含层逐步修正网络的连接权值。通过这样一个不断重复学习与调整的过程，最终可以使得误差信号逐渐接近网络模型设定的目标，此时网络训练停止[6]。

1.2 BAS原理

天牛须搜索(Beetle Antennae Search, BAS)算法[7-8]是一种基于天牛觅食原理来实现多目标函数全局寻化的新算法,其基本原理为:当天牛个体在觅食时，它并不清楚食物的具体位置,而是根据食物的气味强弱来寻找目标。天牛有左右两只长触角,在觅食过程中若左边触角接收到的气味强度大于右边，那么天牛就会飞向左边，反之则飞向右边。基于这一简单生物原理，天牛可以迅速而有效的寻找到食物。BAS算法只注重个体，而不需要知道函数的具体形式以及梯度信息，采用迭代的方式逐步逼近全局最优值，实现快速寻优过程。建模步骤如下

步骤1 建立天牛左右须朝向的随机向量并进行归一化处理。

(1)

式中：rand(·)为随机函数，k代表空间维度。

步骤2 创建天牛左右须空间坐标。

(2)

式中：xl代表第t次迭代时天牛左须的坐标值；xr代表第t次迭代时天牛右须的坐标值；xt代表第t次迭代时天牛的质心坐标值；d0代表天牛左右两须之间的距离。

步骤3 根据适应度函数判断天牛左、右两须接收的气味强度，即求取f(xl)和f(xr)函数值。 其中，f(xl)为天牛左须适应度函数值，f(xr)为天牛右须适应度函数值。

步骤4 判断步骤3中两函数值大小，迭代更新天牛的位置。

xt+1=xt-δt*dir*sign(f(xr)-f(xl))

(3)

式中：δt代表在第t次迭代时的步长因子，sign(·)为符号函数。

1.3 BAS-BP神经网络模型的建立

BP神经网络相比于其他智能算法而言，最显著的优点在于整个网络训练过程中不需要引入新的参数，主要通过误差函数对网络的初始参数进行不断调整。但由于初始权阈值是通过随机方式获取的，所以一旦选择不当则会极大地影响网络训练结果。此外，BP神经网络算法在学习的过程中极易陷入局部最优值，并且对于一些高复杂线性、非线性混合数据处理速度较慢，预测精度不高。因此，本文将采用天牛须搜索先对标准BP神经网络的初始权阈值进行初步优选后，再将其运用到设定好的网络中进行训练，然后构建最终的网络训练模型。该优化算法能够有效地改善网络的训练性能，避免初始参数随机化使网络易陷入局部最优的问题。其具体优化步骤如下[9]

步骤1 建立天牛两须朝向的随机向量，定义搜索空间维度。假设模型结构为m-n-1，有m个输入层神经元，n个隐含层神经元，1个输出层神经元，则空间维度L=m*n+n*1+n+1

步骤2 设置步长因子δ。迭代过程中变步长采用式(4)来计算，其中eta一般取0.95。

δt+1=δt*etat=(0,1,2,…,n)

(4)

步骤3 确定适应度函数。在BAS-BP估算模型中以测试数据的均方误差(MSE)作为适应度评价函数，从而实现空间区域的搜索。其中

(5)

式中：N表示输入样本数，yd代表期望输出值，yi代表实际值。因此，当算法迭代终止时适应度函数的最小值即所求问题的最优解。

步骤4 天牛位置初始化。采用随机方式选取初始参数在[-0.5,0.5]之间的数作为天牛初始位置，并且保存在bestX中。

步骤5 评价适应度。依据适应度评价函数(5)计算天牛初始位置的适应度函数值，并将其保存在bestY中。

步骤6 更新天牛左右须位置。

步骤7 更新最优解。根据天牛两须位置，求解左须适应度函数值f(xl)和右须适应度函数值f(xr)，比较其大小并更新天牛位置。即调整标准BP神经网络的权阈值，并计算此时的适应度函数值，若优于bestY则更新。

步骤8 控制迭代终止。评判适应度函数值是否满足预先设定的迭代精度或是否达到最大迭代次数，若满足则进行下一步，否则返回步骤6继续进行迭代。

步骤9 生成最优解。算法迭代终止时bestX中的解为网络训练的最优解，即BP神经网络的最优初始权阈值。将上述最优解带入标准BP神经网络中进行二次训练，并构建最终的装配式建筑估算模型。

2 工程特征参数的选取

利用BP神经网络模型对装配式建筑项目进行投资估算预测，首先需要解决的核心问题就是根据装配式建筑特点，找出影响其工程造价的重要特征参数。本文通过对传统现浇设计与装配式设计技术经济指标进行对比分析[10]，构建了装配式建筑工程特征指标体系[11](见图1)。通过对两种建造方式的工程项目造价对比，最终将装配式建筑项目工程造价分为土建类、装饰类、电气类、安装类、给排水类。其中以占比最大的土建部分为重点研究对象，最终确定了11个反映装配式建筑投资估算的工程特征向量[12]：基础类型、建筑面积、建筑结构、建筑层数、装配式构件类型、预制构件连接方式、屋面及防水工程、装饰工程、安装、电气及给排水工程、装配率、造价指数，以此作为BP神经网络模型的输入向量。

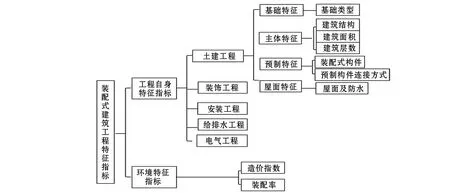
图1 装配式建筑工程特征指标体系

3 算例分析

3.1 网络设计

本文利用一个具有隐层的3层BP神经网络构建装配式建筑工程造价估算模型，输入层节点数为11，隐含层节点数设为50，输出层节点数为1。因此网络结构设置为11-50-1，空间维度为651。初始步长δ设置为3，网络训练达到最大迭代次数100就停止。

3.2 数据处理

本文以安徽省装配式恢复与重建项目为主要研究对象，通过参考大量装配式建筑典型案例[13]并收集相关部门装配式建筑调研资料，最终整理出21组装配式建筑项目数据进行网络训练，其中20组作为训练样本，1组作为检验样本，各装配式建筑项目均以一个单项工程为单位进行数据分析。由于原始样本数据之间存在显著的量纲差异，因此需要对样本数据进行相应的预处理。本文先对装配式建筑工程特征进行数值量化(见表1)。然后再对收集的样本数据根据工程特征量化表进行数值量化(见表2)。最后通过线性归一法对数据进行预处理，归一化公式见式(6)[14]。

(6)

表1 工程指标定量化表

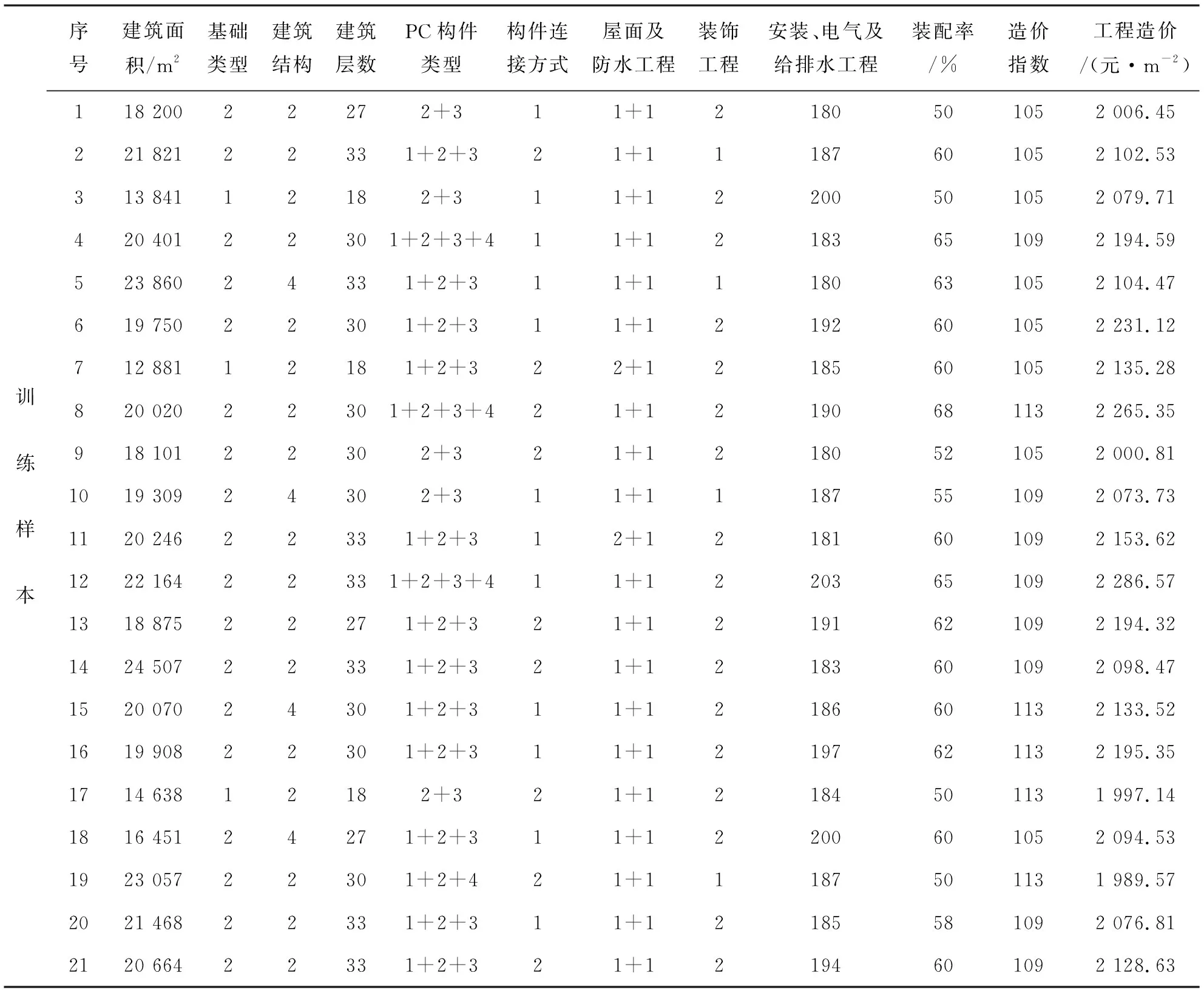
表 2 原始训练数据样本库

3.3 MATLAB仿真及对比分析

采用MATLAB 2016a软件对标准BP神经网络及BAS-BP神经网络进行样本训练，最终训练结果如下图2和图3所示。

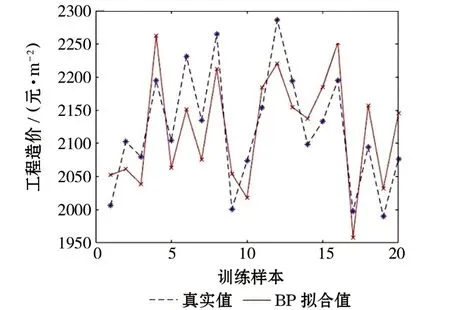
图2 BP神经网络训练集拟合效果

图3 BAS-BP神经网络训练集拟合效果

由图2和图3可以清晰看出，相比于标准BP神经网络，BAS-BP神经网络的拟合结果走势更加平稳且逼近真实值。因此，改进后的BP神经网络模型具有一定的优化效果。

为了测试BAS-BP神经网络估算模型较其他优化算法模型在装配式建筑项目投资估算应用中是否具有优越性，本文选择GA-BP神经网络模型和PSO-BP神经网络模型与BAS-BP神经网络模型进行估算精度对比。主要从相对误差均值、迭代过程中CPU运行时间以及训练步数3个角度对模型的精度进行描述[15]。训练结果如图4和图5所示。

图4 GA-BP神经网络训练集拟合效果

图5 PSO-BP神经网络训练集拟合效果

由图4和图5可以看出，PSO和GA优化的估算模型预测曲线也较贴合真实值。将标准BP神经网络、GA-BP神经网络、PSO-BP神经网络及BAS-BP神经网络的训练及测试性能进行对比，对比结果如表3所示。

表3 不同模型性能对比

从表3中可以看出BAS-BP神经网络模型比标准BP神经网络模型的整体效果更好，其中PSO-BP和BAS-BP对训练样本集的拟合效果较好，网络误差精度相差不大，但BAS-BP的训练速度远大于PSO-BP。GA-BP拟合效果次之，并且收敛速度非常慢。从整体误差精度、训练时间及收敛速度上来看BAS-BP效果最佳，所以BAS-BP神经网络估算模型的构建有一定的优化效果，并且估算误差满足行业允许要求，因此优化模型应用于装配式建筑投资估算控制是合理可行的。

4 结论

(1)装配式建筑项目影响因素众多，因而其投资估算需要合理有效的选取特征因素，其中“显著性成本”与BAS-BP神经网络相结合对于控制装配式建筑投资估算会是一个值得的尝试。

(2)基于BAS优化的 BP 神经网络模型预测效果优于随机状态下 BP 神经网络，估算精度也上有明显提高。同时，与其他融合后的优化算法相比，迭代速度有明显提高。因此 BAS-BP神经网络模型的建立对于装配式建筑投资估算研究有一定实际价值。

(3)投资估算模型的有效建立需要丰富的项目数据为支撑。装配式建筑作为新型建造方式在实际中的应用还有一定限制，工程历史数据较少。因此，其项目数据库有待进一步完善。

(4)有效控制装配式建筑投资估算，一方面要完善装配式生产标准，推进装配式建筑实现专业化和规模化。另一方面要不断创新投资估算方法，建立更加完善有效的装配式建筑投资估算模型。