基于面积折减等效模型的光电倍增管水下内爆机理研究*

孟令存，闫 明，杜志鹏，张 磊

（1. 沈阳工业大学机械工程学院，辽宁 沈阳 110870；2. 海军研究院，北京 100161）

在深水环境下工作的光电倍增管（photomultiplier tube，PMT），其玻璃外表面承受高静水压力，当压力载荷超过玻璃壳体的结构强度时，PMT 被压溃使水流向中心流动，流体的水下压力势能转化为动能，当水流压缩至最小限度时，高速流体碰撞产生水锤型冲击，发生内爆[1-4]，产生内爆冲击波。水下内爆冲击波会对周围的PMT 造成破坏，引发相邻的PMT 发生殉爆。2014 年，美国深海科研潜艇“Nereus”号在执行深海作业时，潜艇的中空陶瓷浮力装置在巨大静水压力下被压溃，发生内爆，使其遇难。在高能物理研究领域，脆性材料[5]制成的内部真空的PMT 被用来进行粒子探测，工作在深水环境中，容易发生内爆；2001 年，日本超级神冈中微子实验站发生PMT 殉爆事故，此次事故炸毁将近8 000 个PMT，直接经济损失高达3 000 万美元，中微子研究遭受重大挫折[6]。我国将建设世界领先地位的江门中微子实验站，该实验站拟采用16 000 只直径约为500 mm 的PMT 作为探测器，其最大工作水深为40 m。根据国外相关事故的经验教训和江门中微子探测器的实际工作要求，为防止PMT 殉爆的发生，探索PMT 内爆机理具有重要的应用价值和实际意义。

国内外对水下内爆进行了诸多研究。Diwan 等[7]在大型可加压容器罐内进行了2 次0.69 MPa 静水压下PMT 内爆试验，得到了PMT 内爆过程高速摄像及内爆冲击波压力时域曲线，并用LS-DYNA 对其进行了数值模拟，但计算结果与试验结果差别较大；Gish 等[8]在可加压容器罐中进行了金属圆柱壳内爆试验，并结合数值模拟研究了圆柱壳长度、直径和厚度对内爆冲击波的影响；杜志鹏等[9]将水下爆炸气泡动力学与水下内爆相结合，基于能量守恒关系，推导出不可压缩流体中球形容器内爆理论模型，并利用该理论模型分析了容器尺寸、静水压力对内爆冲击波压力峰值、气泡溃灭时间周期的影响规律；黄治新等[10]基于应力波原理，提出一种在大型钢制压力罐内进行PMT 内爆试验的试验方法，并通过此方法成功测得PMT 内爆发生过程高速摄像及内爆冲击波。

上述研究主要针对水下内爆特性进行了试验与数值模拟，但对于PMT 内爆并没有有效的防护。本文开展了PMT 水下内爆试验，用于验证PMT 内爆简化模型模拟水下内爆的准确性；并通过有限元计算的方式探究水流涌入面积对内爆冲击波的影响，提出了当PMT 发生破碎时，减小水流涌入面积能有效减小内爆冲击波强度的内爆防护原理。

1 PMT 内爆简化模型的数值计算

1.1 PMT 内爆试验与内爆简化模型

PMT 实物如图1 所示，其形状如灯泡，PMT 玻璃外壳厚度为5 mm，头部球体部分外径为0.508 m，尾部直径为0.1 m，总高度约为0.7 m，内部真空体积为6.992×10-2m3；PMT 内爆试验在如图2 所示直径为3 m的可加压密封钢制容器罐内进行，压力罐侧面透明视窗用于放置照明和高速摄影设备，罐内设有工作平台、液压式挤压装置。试验中共布置4 个PCB 动压传感器，F1 位于PMT 正上方，距PMT 中心0.41 m 处；F2 位于PMT 赤道平面，靠近压力罐入口处，距PMT 中心0.55 m 处；F3、F4 分别位于PMT 赤道平面，远离压力罐入口处，距PMT 中心0.55、1.35 m处。试验前，罐中装入水，罐上方预留出适量空气，考虑PMT 殉爆防护安全余量，利用空压机对压力罐中施加0.5 MPa 压力模拟PMT 深水工作环境；试验时，挤压装置模拟外界恶劣环境挤压PMT 发生内爆，内爆发生过程通过高速摄像（3 000 Hz）进行记录，压力数据利用杭州亿恒数据采集系统（采样率为1 MHz）进行采集，试验成功测得PMT 内爆过程及4 组内爆冲击波压力数据。

完成PMT 内爆试验后，对PMT 内爆过程进行分析。由内爆试验高速摄影可知整个内爆过程如图3所示，可将其分为4 个典型阶段：（1）挤压阶段；（2）裂纹传播阶段；（3）整体压溃形成冲击波阶段；（4）冲击波传播与碎片飞散阶段。挤压装置挤压PMT 产生局部初始裂纹，初始裂纹瞬间传遍整个玻壳而发生坍塌，外部高压水流迅速内涌发生碰撞产生内爆冲击波。高速摄像充分展现了PMT 内爆发生过程和冲击波产生过程，对水下内爆数值模拟具有一定的指导意义。

图1 光电倍增管实物图Fig.1 Picture of photomultiplier tube

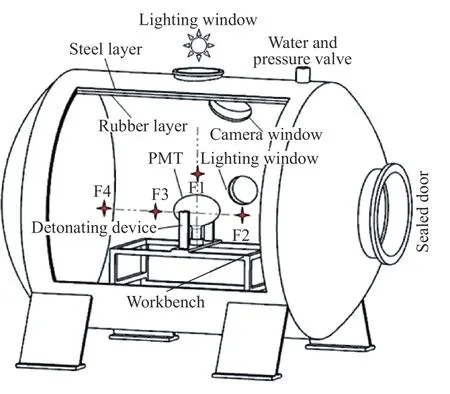
图2 内爆试验装置示意图Fig.2 Schematic of test device for implosion

图3 PMT 内爆过程Fig.3 Process of the PMT implosion

下面用有限元方法模拟PMT 内爆过程，由高速摄影看到PMT 产生局部初始裂纹后会瞬间传遍整个玻壳而发生坍塌，因此进行简化数值模拟时，忽略PMT 玻壳的影响，只单独计算外部水域流场，按体积等效的方式将PMT 等效为半径为0.25 m 的真空球体。图4 为PMT 内爆有限元模型中部截面图，整个水域半径为1.7 m，采用六面体欧拉网格，单元类型为EC3D8R，水域节点共计619 393 个，单元共计613 872 个；蓝色部分欧拉网格赋予水材料属性，水采用Grüneisen 状态方程描述，密度为1 000 kg/m3，us-up直线截距（声速）为1 484 m/s，水黏度为1×10-3Pa·s；红色部分欧拉网格设置无材料填充，默认为真空状态，真空半径为0.25 m，用于模拟PMT。利用初始应力的方法设置蓝色部分水域初始静水压力为0.5 MPa，水域外边界设置冲击波无反射、流体自由流入、流出边界条件，模型中压力测点S1～S4 与内爆试验测点F1～F4 位置相对应，最后通过显示动态分析步（explicit）进行求解。将简化数值模型的计算结果与试验结果相对比，验证简化模型的合理性。

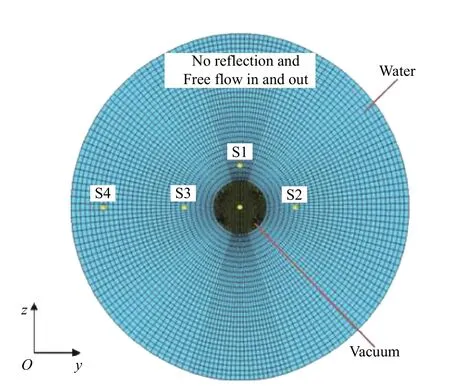
图4 内爆数值计算模型Fig.4 Implosion simulation model

1.2 数值模拟与试验冲击波压力对比分析

以冲击波最大峰值时刻为基准，将数值计算所得各测点的冲击波压力数据与对应试验测点压力数据绘制曲线如图5 所示。试验中各测点压力数据首先产生内爆冲击波峰值，最大峰值过后经过2 ms，出现第2 个压力峰值，峰值约为2 MPa，这是由于压力罐壁反射冲击波导致的；由于压力罐直径为3 m，按冲击波传播速度为1 500 m/s 计算，罐壁反射冲击波应经过2 ms 返回至压力测点，这与试验所测得的数据相吻合，证明了冲击波测量的准确性。数值模型中冲击波压力数据与试验数据相比，波形较为平滑，振荡较少，脉宽偏小；最大压力峰值过后无反射冲击波峰值产生，这是由于数值模型设置了无反射边界条件，因此所得压力数据无反射波形。将数值模型中各测点冲击波压力峰值与相对应试验压力峰值列于表1，计算值与试验值最大相差13.4%。

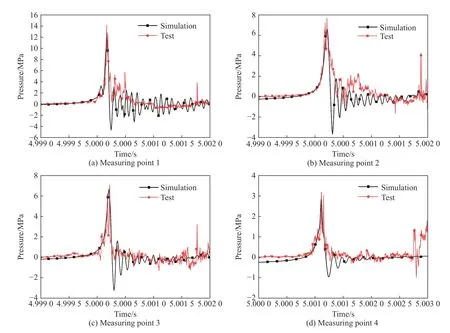
图5 数值模拟与试验测点压力对比Fig.5 Comparison of the simulation and test pressures of the measuring points

表1 数值模拟与试验所得的测点压力峰值对比Table 1 Difference between the simulation and test peak pressures of the measuring points

1.3 数值模拟与试验冲击波比冲量对比分析

通过对比数值模拟与试验压力冲击波数据可知，与计算相比试验压力数据曲线存在反射冲击波峰值。为消除试验压力数据反射冲击波对比冲量的影响，提高可比性，对计算与试验数据，均取内爆产生的最大波峰及其之前的压力数据进行积分，得到如图6 所示的试验与计算内爆冲击波比冲量对比曲线。

图6 数值模拟与试验测得的比冲量对比Fig.6 Comparison of the simulation and test impulse of the measuring points

试验数据比冲量在积分区域内均呈逐渐增大至平稳的趋势，计算数据比冲量出现负值是由于压力数据存在负压导致的；取计算与试验内爆冲击波比冲量数据最大值与最小值的差值作为内爆冲击波比冲量峰值，将试验与计算数据比冲量峰值列于表2，可看出测点1、2 通过计算得到的冲击波比冲量峰值与试验偏差较大，这是由于测点1、2 试验压力数据最大峰值后出现较大振荡干扰导致的。通过以上分析可知，与内爆试验相比，内爆数值计算所得冲击波压力峰值最大相差13.4%，冲击波比冲量峰值最大相差24.8%，这对内爆数值计算来说，是可以接受的，满足实际工程需求。

表2 数值模拟与试验所得的测点比冲量峰值对比Table 2 Difference between the simulation and test peak impulse of the measuring points

1.4 水域流场及速度变化

下面对内爆简化模型的水域流场与流速进行分析。欧拉网格具有与材料完全隔离的特性，欧拉网格中材料的体积分数以不同的颜色区分，红色代表材料体积分数为1，即水填满整个网格；蓝色代表材料体积分数为0，即没有水填充。内爆简化模型计算中，水域流场变化过程如图7 所示。图7（a）为内爆初始状态，蓝色代表PMT 真空区域，红色代表外部水域，其初始静水压为0.5 MPa；图7（b）、（c）为PMT破碎后，外部水流迅速内涌发生内爆的过程，可看到水流从四周均匀涌向球心；图7（d）为内涌水流碰撞产生冲击波的瞬间。PMT 内爆简化模型模拟内爆发生过程共经过10.25 ms，与试验高速摄像拍摄的PMT 内爆过程及发生内爆的时间相近。数值计算中水流前锋速度变化过程如图8 所示，在整个过程中水流前锋速度逐渐增加，内涌高速水流碰撞前速度达324.9 m/s，说明PMT 内爆发生前碰撞水流具有很大的动能。

图7 水域流场变化过程Fig.7 Evolution of the water field

图8 水流前锋速度变化过程Fig.8 Evolution of the water front velocity

通过以上PMT 内爆数值模拟与试验对比可知，PMT 内爆数值简化模型在冲击波压力、比冲量、水域流场方面，能够较为全面、准确地模拟PMT 内爆真实物理情形。

2 水流涌入面积对内爆的影响

2.1 定义面积折减因数

在PMT 水下内爆数值模拟方法正确建立的基础上，为避免PMT 殉爆的发生，下面利用数值模拟对内爆冲击波的影响因素进行研究。PMT发生内爆时，玻壳整体破碎向内坍塌，外部水流从四周涌入，发生碰撞产生冲击波。为探究水流涌入面积对内爆的影响，假设PMT 瞬间破碎后，外部存在相同直径的有机玻璃防护装置，如图9所示，其中R 为等效半径，H 为球冠高度，D 为防护装置破口直径。

定义无量纲面积折减因数α 来表示防护装置破口程度：

式中：Sa=4πR2，为PMT 等效表面积；Sb=4πRH，为防护装置破口表面积，具体数值列于表3。

图9 PMT 防护装置示意图Fig.9 Schematic diagram of PMT protection device

表3 破碎面积具体值Table 3 The value of break area

2.2 面积折减内爆简化模型

当面积折减因数α 为0.9、0.8、0.7 时，需在内爆简化模型（α=1）中加入防护装置模型，如图10 所示，此时应采用欧拉-拉格朗日耦合分析方法，有机玻璃防护装置利用拉格朗日网格描述，采用厚度为10 mm的壳单元。其密度为1 180 kg/m3，弹性模量为2.77 GPa，泊松比为0.376，并约束其所有节点自由度（防护装置保持固定），其余初始、边界条件与内爆简化模型相同。

图10 PMT 防护装置等效模型Fig.10 Equivalent models of the PMT protection device

为探究不同面积折减因数下冲击波压力在水中传播情况，在PMT 防护装置一侧缺口对应的水域轴线上布置一系列压力测点，如图11 所示，在测点A1 至A29 连线上等间距布置29 个压力测点（A1～A29），其中A1 为PMT 防护装置圆周处测点。

2.3 面积折减内爆数值模拟结果分析

2.3.1 水域流场分布

不同面积折减因数下高速水流碰撞瞬间流场分布如图12 所示，同理，以颜色区分欧拉网格中水的体积分数。由水域流场分布可直观地看到，与PMT 整体破碎内涌水流四周碰撞相比，随着防护装置破口面积的减小，真空区域内涌水流碰撞量随之大幅度减少，只是水流前锋局部碰撞产生冲击波，这可能导致冲击波强度发生变化。

图11 水域测点分布示意图Fig.11 Distribution of measuring points in water field

图12 水域流场分布Fig.12 Distribution of water field

2.3.2 内爆冲击波压力分布及强度分析

下面对不同面积折减因数下冲击波强度进行分析：图13 为各面积折减因数下A1 测点处的冲击波压力时域曲线。可看出随着防护装置破口面积减小，PMT 圆周处测点的冲击波压力峰值迅速减弱。但冲击波脉宽基本不变；同时，随着防护装置破口面积的减小，水流碰撞发生内爆的时刻也相应提前。进一步对冲击波压力峰值进行分析，取各面积折减下测点A1～A29 冲击波压力峰值，以冲击波压力峰值为纵坐标，测点距球心的距离为横坐标，绘制曲线如图14 所示，为了曲线表达清晰，每间隔一个测点进行标记显示。以PMT 球心为内爆中心，可明显观察到内爆压力峰值随与测点距离的增大而逐渐衰减，在0.25～0.40 m 范围内，内爆压力峰值迅速衰减，0.40 m 以外其内爆压力峰值衰减相对较慢，在1.60 m 处内爆压力平稳回归到约2 MPa；最重要的是随着面积折减因数的减小，防护装置破口面积减小，同一测点水流内涌碰撞产生的冲击波压力峰值均大幅度地减弱，这可能与内涌水流碰撞量的减少有关，但也可能与水流前锋碰撞速度的变化有关。

图13 A1 测点冲击波压力变化Fig.13 Shock wave pressures varied with time at measuring point A1

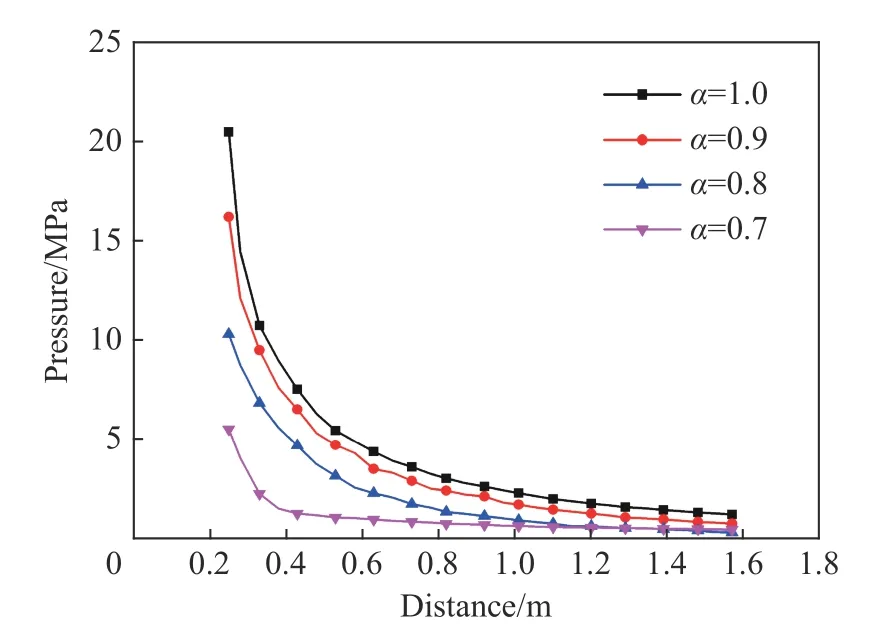
图14 冲击波压力峰值分布Fig.14 Distribution of peak pressure

对内爆冲击波的影响因素进行进一步分析：图15 为各面积折减因数下内爆发生前的水流前锋速度随时间变化曲线，可看出水流前锋速度在前期增长缓慢，后期迅速增加；防护装置破口面积越小，水流前锋速度增加越快，但其碰撞前速度相差不明显，说明防护装置破口面积对内涌水流前锋最终碰撞速度值影响较小。各面积折减因数下，A1 测点压力峰值与内涌水流前锋速度变化如图16 所示。在防护装置破口面积变化30%情况下，A1 测点内爆压力峰值变化73.6%，对应的内涌水流前锋速度变化仅为13.9%，说明随着防护装置破口面积的减小，内爆冲击波压力峰值大幅度减弱主要是内涌水流碰撞量减少导致的，而内涌水流前锋最终碰撞速度对其影响较小。降低内爆冲击波压力峰值为PMT 内爆防护提供了重要思路。

图15 水流前锋速度Fig.15 Velocities of the water fronts

图16 压力峰值与水流前锋速度变化Fig.16 Variation of the peak pressure and the velocity of water front

3 结 论

（1）以PMT 内爆试验为基础，通过数值模拟再现了PMT 内爆过程，对比数值模拟与试验结果可知：数值模拟得出的PMT 内爆发生过程、冲击波压力峰值和冲击波压力比冲量与试验吻合较好，验证了PMT 内爆简化模型的合理性和适用性，提出了一套PMT 内爆数值模拟方法。

（2）在此基础之上，提出了基于面积折减等效模型的PMT 内爆计算方法，通过等效模型分析了不同面积折减因数对PMT 内爆冲击波的影响，得出基于面积折减等效模型的PMT 水下内爆机理：随着防护装置破口面积的减小，水流碰撞引起的PMT 内爆发生时刻相应提前，内爆产生的冲击波脉宽基本保持不变、冲击波峰值明显减小，这主要是随着防护装置破口面积的减小使内涌水流碰撞量减少导致的，而内涌水流前锋最终碰撞速度对其影响较小。