浅谈如何更好地理解V排=SΔh

余艳

在讲授沪教版九年级物理第六章第四节《阿基米德原理》这一节新课时，笔者发现正确理解“V排”是理解阿基米德原理和解题的关键所在.通过液面升高的深度来求解“V排”也是教师正常的教学思路，但是学生往往只知其然，不知其所以然.下面笔者就自己在教学方面的理解以及查阅相关资料后的感悟谈一谈如何更好地理解V排=SΔh（S为柱状容器的底面积，Δh为液面升高的深度）.

情况1：假设物体密度大于等于液体密度.

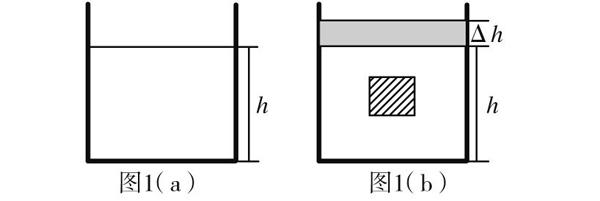
我们先做一个假设.假设物体高度小于原有液体深度.当物体密度大于等于液体密度时，物体将处于沉底或悬浮状态，也就是物体将完全浸没在液体中，设容器原有深度为h的某种液体，如图1（a）所示，当物体完全浸没时，液面升高深度为Δh，如图1（b）所示.完全浸没的这种类型，学生很容易理解V排等于V物，但V排为什么等于SΔh却说不清楚.如果可以以数学证明题一般进行论证，不仅更具有信服力，而且能为培养学生理科学习的严谨性打下基础.下面简要阐述证明过程.

证明：原容器中液体的总体积V液=Sh（1）;

物体完全浸没后液体的体积不变，此时容器的总体积V=V液+V物（2）;

此外将容器和物体看成整体，总体积V=S（h+Δh）（3）.

即V液+V物=S（h+Δh）（4）

將（1）代入（4）可得，V物=SΔh，即V排=SΔh.

情况2：假设物体密度小于液体密度.

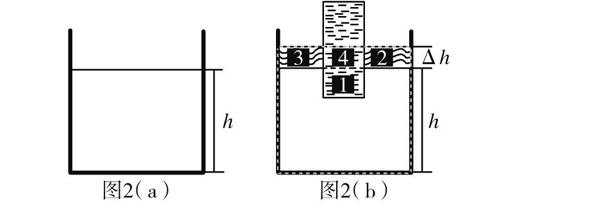
上述假设仍成立时，当物体密度小于液体密度时，物体将处于漂浮状态，依旧设容器原有深度为h的某种液体，如图2（a）所示，当物体漂浮时，液面升高深度为Δh，物体底面积为S物，如图2（b）所示.图2（b）所指数字1表示物体完全没入的部分，数字2和3表示液体升高的深度部分，数字4表示表示物体夹在最初液面和最终液面之间的部分.它们的体积分别记为V1，V2，V3，V4.学生会直观地理解V2+V3是排开液体的体积大小，那么对应的面积S′应该是2和3对应的底面积，也就是S-S物，利用面积差求出V排，V排=（S-S物）Δh.靠直观的理解往往出现假象，以严密的证明过程进行论述加以证明才可以正确理解V排到底是哪一部分.下面我们仿照第一种情况进行论证上述结论是否正确.

证明：已知原容器中液体的总体积V液=Sh（1）;物体漂浮在液体表面，此时图2（b）虚线框内的总体积V=V液+V排（2）;此外将虚线框内的液体和物体看成整体，总体积V=S（h+Δh）（3），即V液+V排=S（h+Δh）（4）.将（1）代入（4）可得，V排=SΔh.这与我们通过直观的臆测不符合，也就是我们通过合理的论证证明出了V排依旧等于SΔh，从图中可以发现SΔh=V2+V3+V4（5），因此V排并不是V2+V3这两部分，其实是V2+V3+V4这三部分.

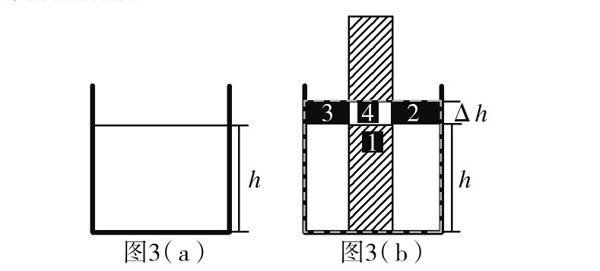
拓展延伸：有以上证明作为基础，我们可以继续分析当物体密度大于液体密度时，且物体高度高于原有液体高度时，V排=SΔh是否还成立？如图3所示，已知条件同上，我们依然采用前面的证明过程，再次论证.

证明：已知原容器中液体的总体积V液=Sh（1）;

物体沉在容器底部，此时图2（b）红色虚线框内的总体积V=V液+V排（2）;此外将红色虚线框内的液体和物体看成整体，总体积V=S（h+Δh）（3）.即V液+V排=S（h+Δh）（4）.将（1）代入（4）可得V排=SΔh，我们通过相同的论证方法得出了V排依旧等于SΔh.

综上所述，无论物体在液体中处于什么状态，V排=SΔh，都是成立的.