基于小波包分解和PSO-BPNN的滚动轴承故障诊断

鞠晨， 张超， 樊红卫，3， 张旭辉，3， 杨一晴， 严杨

(1.神华神东煤炭集团有限责任公司 技术研究院， 陕西 神木 719315；2.西安科技大学 机械工程学院， 陕西 西安 710054；3.西安科技大学 陕西省矿山机电装备智能监测重点实验室， 陕西 西安 710054)

0 引言

煤矿旋转机械工作载荷时变，常伴随冲击信号，致使其滚动轴承故障频发，约占煤矿机械故障的30%[1-2]，严重影响煤矿生产安全，因此对煤矿旋转机械滚动轴承进行故障诊断具有重要意义。滚动轴承故障诊断过程主要包括信号特征提取和故障类型识别两部分，有效的信号特征提取是故障准确识别的基础。

煤矿旋转机械实际运行工况复杂，采集的滚动轴承振动信号常表现为非平稳、非线性[3-4]。常规的信号特征提取一般采用时频分析方法，如傅里叶变换、小波变换等。但傅里叶变换难以适用于非平稳信号；小波变换存在高频部分疏漏问题，易出现信号分析不完全导致信号有效特征丢失的问题[5]。小波包分解是在小波变换的基础上发展起来的，能适应非平稳信号，对信号的全频带进行更精细的分析，提高信号分辨率[6]。张猛等[7]利用小波包分解在全频段对滚动轴承振动信号进行多层次的频带分解，增强故障冲击信号，能较好地提取轴承早期故障特征。郭伟超等[8]对轴承振动信号进行小波包分解，得到不同频率区间的子频带能量作为特征向量，并结合主成分分析方法对特征向量进行降维，获得增强的故障特征。

在故障类型识别方面，BP神经网络(Back Propagation Neural Network，BPNN)因具有优良的多维函数非线性映射能力及较强的任意复杂模式的分类能力而得到广泛应用[9-10]。但采用BPNN进行轴承故障识别时，其性能容易受网络初始权值和阈值的影响，存在收敛速度慢及局部收敛等问题[11]。粒子群优化(Particle Swarm Optimization，PSO)算法是模仿鸟群在觅食中个体对信息的共享使群体运动最优的过程[12-13]，侯一民等[14]引入PSO算法对BPNN进行优化，增强了网络全局搜索能力，提高了收敛速度和准确度。

因此，本文将小波包分解和PSO-BPNN相结合进行滚动轴承故障诊断。采用小波包分解提取滚动轴承振动信号有效特征，利用PSO算法优化BPNN初始权值和阈值，通过PSO-BPNN对滚动轴承故障状态进行识别。

1 基于小波包分解的信号特征提取

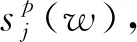
(1)

滚动轴承原始振动信号经过j层小波包分解得到2j个不同频率区间的子频带，信号全部信息完整保留，避免了信号中有用特征信息的丢失。

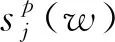
(2)

提取各子频带能量并进行累加得到信号总能量Ej,T，经归一化处理后，可得各子频带能量在信号总能量的占比β1及信号总能量与不同故障状态下信号总能量最大值Ej,Tmax的比值β2：

(3)

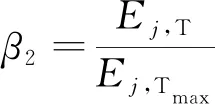
(4)

表征滚动轴承状态的特征向量为

β={β1,β2}

(5)

2 PSO-BPNN

利用PSO算法的群体寻优策略来确定BPNN权值和阈值的最优初始值。假设在优化BPNN初始权值或阈值的M维可行解空间中存在一个由B个粒子组成的粒子群，其中每个粒子表示BPNN初始权值或阈值的一个最优解，每个粒子的3个主要特征为适应度值、位置和速度。适应度值由适应度函数计算得到，表示粒子的优劣程度。在M维空间中，令第i(i=1，2，…，B)个粒子的位置向量为Xi={Xi,1,Xi,2,…,Xi,M}(Xi，m为第m维空间中第i个粒子的位置,m=1，2，…，M)，速度向量为Vi={Vi,1,Vi,2,…,Vi,M}(Vi，m为第m维空间中第i个粒子的速度)，在当前搜索空间中个体最优位置向量为Pi={Pi,1,Pi,2,…,Pi,M}(Pi，m为第m维空间中第i个粒子的个体最优位置)，在整体搜索空间中全局最优位置向量为Pg={Pg,1,Pg,2,…,Pg,M}(Pg，m为第m维空间中粒子的全局最优位置)。计算粒子在第t次迭代后的速度Vi,m(t)和位置Xi,m(t)所对应的适应度值，通过跟踪粒子个体最优位置Pi,m(t)和全局最优位置Pg,m(t)，依据式(6)、式(7)对粒子的速度和位置进行迭代更新，计算第t+1次迭代后粒子的速度Vi,m(t+1)和位置Xi,m(t+1)所对应的适应度值。按上述方式进行迭代更新，当迭代终止时，对比每一次迭代的适应度值，从而得到全局最优适应度值，并找到其所对应粒子的位置。

Vi,m(t+1)=ω(t)Vi,m(t)+c1r1(Pi,m(t)-

Xi,m(t))+c2r2(Pg,m(t)-Xi,m(t))

(6)

Xi,m(t+1)=Xi,m(t)+Vi,m(t+1)

(7)

式中：ω(t)为惯性权重；c1，c2为学习因子；r1，r2为[0，1]区间的随机数。

3 滚动轴承故障诊断

基于小波包分解和PSO-BPNN的滚动轴承故障诊断步骤如下。

(1) 将多组不同滚动轴承故障实验采集的振动信号样本划分为训练集和测试集，并对振动信号样本进行小波包分解，得到各子频带能量及信号总能量，经归一化处理后获得表征滚动轴承状态的特征向量。

(2) 确定BPNN参数，通过计算得到粒子群搜索空间维度。

(3) 初始化粒子群参数，包括粒子数、最大迭代次数、粒子最大速度、初始种群位置范围，取训练实际输出与期望输出的均方误差函数作为PSO算法适应度函数。

(4) 计算对比每个粒子的适应度值，并通过式(6)、式(7)迭代更新粒子的速度与位置，直到达到最大迭代次数，最终得到全局最优位置，同时将粒子群位置映射得到BPNN最优初始权值和阈值。

(5) 将训练集所提取的特征向量作为BPNN输入，同时代入最优初始权值和阈值进行网络训练，通过计算BPNN的反向误差对权值和阈值继续调优，直至满足训练目标，得到训练好的PSO-BPNN。

(6) 通过训练好的PSO-BPNN进行滚动轴承故障诊断，判别滚动轴承故障类型。

4 实验验证

4.1 实验方案

为更好地模拟煤矿旋转机械的复杂工况，以某机械传动装置为测试平台，取距离电动机端较远的平行轴齿轮箱第二级传动轴输出端滚动轴承为实验对象。滚动轴承型号为ER-16K，电动机转速为1 800 r/min，加速度传感器灵敏度为103 mV/g(g为重力加速度)，采样频率为10.24 kHz。在正常与故障状态下采集轴向振动信号共500组，其中正常滚动轴承振动信号100组，内圈故障、外圈故障、滚动体故障及混合故障(图1)下振动信号各100组，将采集的振动信号样本按3∶2分为训练集和测试集。

图1 滚动轴承故障类型Fig.1 Fault type of rolling bearing

4.2 参数设置

(1) 小波包分解参数。选取小波基为sym8小波，分解层数为3层。

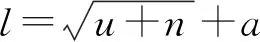
(3) PSO算法参数。粒子数B=20；粒子群速度取值范围为[-1，1]，粒子群位置取值范围为[-1，1]；粒子群搜索空间维度M=(u+1)l+(l+1)n=200；根据经验取c1=c2=1.499 45；最大迭代次数tmax=20；考虑到惯性权重ω(t)大小与PSO算法全局搜索能力呈正相关关系，与局部搜索能力呈负相关关系，为平衡全局搜索能力和局部搜索能力，ω(t)随迭代次数的增加从0.9线性递减至0.4(式(8))。

(8)

式中ωmax，ωmin分别为惯性权重最大值、最小值。

4.3 结果分析

图2 不同状态下小波包能量分布Fig.2 Wavelet packet energy distribution under different states

将特征向量作为BPNN与PSO-BPNN的输入并进行网络训练，得到均方误差曲线，如图3所示。可看出BPNN在训练初期收敛速度较快，但在中期易陷入局部最小值，迭代793次才达到预期目标；PSO-BPNN在训练迭代348次时达到预期目标，有效减少了网络迭代次数，提高了故障诊断效率，同时避免了局部极小值情况的出现。

(a) BPNN

(b) PSO-BPNN

将测试集分别代入BPNN与PSO-BPNN进行故障诊断，结果见表1。可看出PSO-BPNN平均故障诊断准确率为93.5%，BPNN平均故障诊断准确率为89.0%，PSO-BPNN相比BPNN在滚动轴承故障诊断准确率方面有明显提升。

表1 故障诊断准确率Table 1 Fault diagnosis accuracy

5 结语

提出了一种基于小波包分解和PSO-BPNN的滚动轴承故障诊断方法。根据滚动轴承不同故障状态下振动信号频带能量分布的差异，通过小波包分解进行能量特征提取，避免了信号高频部分有效特征的丢失；利用PSO优化BPNN的初始权值和阈值，通过PSO-BPNN进行故障类型识别，提高了故障诊断准确率及效率。实验结果验证了该方法的有效性。