基于新型栅格启发式算法的矿井机器人路径规划

王鹤， 陈静， 滕瑛瑶

(河南工程学院 机械工程学院， 河南 郑州 451191)

0 引言

为了避免煤矿次生灾害对被困矿工及救护人员造成严重伤害，进一步提高救援工作效率和成功率，机器人路径规划问题已成为矿井类机器人研究的核心内容之一[1-2]。为了使机器人可以准确找到事故发生地点，并确认安全路径营救被困矿工，寻找一条距离最短、耗时最少的路径非常重要[3-4]。

在研究机器人路径规划[5-7]时，通常将其运动区域抽象简化成若干个形状规则、大小相同的栅格，以栅格的特征信息描述实际地形。栅格法[8-11]对障碍物的适应能力较强，大大降低了工作环境建模的复杂性。研究者通常选择正方形作为栅格形状，在正方形栅格化的工作地图中，当机器人位于某个栅格时，沿水平或竖直方向和沿对角线方向移动。在实际路径规划中，当遇到障碍物时，若沿对角线方向移动，易与障碍物发生碰撞；机器人在绕障和平稳性等方面的能力较差[12-13]；矿难发生后在实时探测过程中每步消耗的时间无法唯一确定，这对救援造成重大影响。针对上述问题，本文提出了以正六边形栅格化的工作地图为基础，结合改进的启发式路径搜索算法对多个并行移动的机器人进行路径规划的方法，能够有效减少井下多个机器人并行工作的路径长度及探测救援时间，为矿难发生后救援工作的开展争取了宝贵时间。

1 2种地图模型对比分析

将机器人的工作空间分别进行正方形和正六边形栅格化，如图1所示。图中圆圈为机器人，白色栅格为自由栅格，黑色栅格为静态障碍物。在正六边形栅格(即蜂窝栅格)化的工作地图中，机器人可移动的方向最多有6个，如图1(b)所示，即使相邻栅格有障碍物，沿其余任一方向移动时，也不会出现在正方形栅格中沿对角线方向移动可能与障碍物发生碰撞的情况，安全性更高。

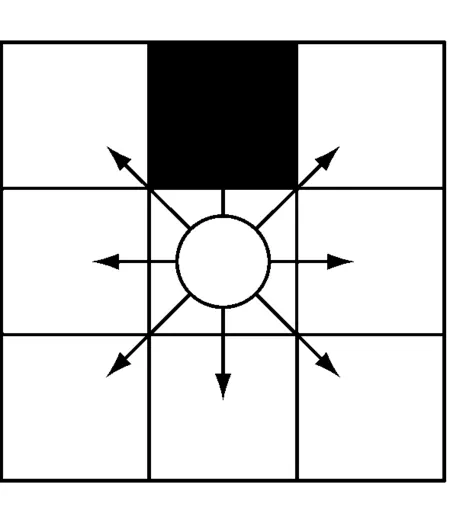
(a) 正方形

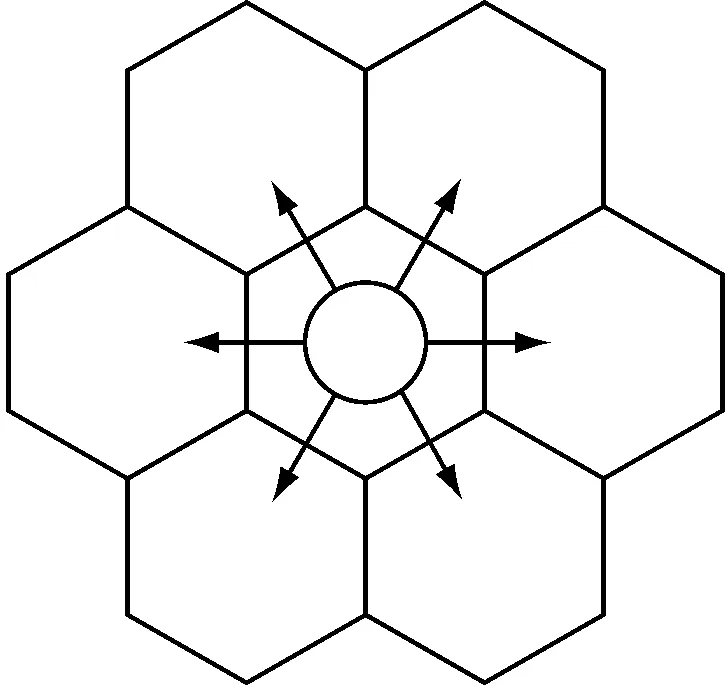
(b) 正六边形

假设在同一工作环境下的正方形和正六边形地图中，单个机器人移动1个栅格位置的距离相同，对其运动性能做比较。

(1) 绕障转角。在遇到静态障碍物时，机器人在传统的正方形栅格地图中移动时，转角为90°，而在正六边形栅格地图中的转角仅为60°，如图2所示。可见，当遇到静态障碍物需要转弯时，在正六边形栅格地图中转角较小，能够提高机器人运动的安全性[7-8]。为提高运动平稳性，在路径规划过程中，不仅要减小转角，也要尽可能减少机器人转向次数。

(a) 正方形栅格

(b) 正六边形栅格

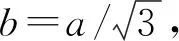
(3) 最优路径。图3为同一工作空间的正方形和正六边形栅格地图。最优路径以付出代价来衡量，付出代价越少，则路径最优。对于单个机器人路径规划来说，其路径越短，耗时也越短。因此单个机器人路径规划目标就是其路径长度代价最小。设机器人移动1个栅格的路径长度代价为w，那么1条路径的长度代价为nw(n为自然数)。对于正方形栅格地图，1条路径的长度代价即起点与终点之间的曼哈顿距离[14-15]。在正六边形栅格中，从起点开始沿靠近终点且与水平相交60°方向移动，直至移动到与终点同一行的栅格，将该栅格与起点之间的距离定义为LS，该栅格和终点之间的距离定义为LD。在正六边形栅格地图中，将上述2个距离之和L=LS+LD定义为变形曼哈顿距离。

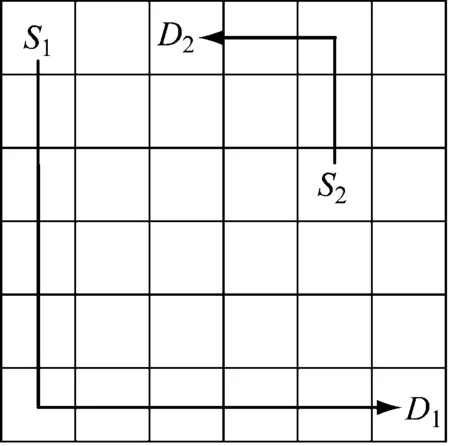
(a) 正方形栅格

(b) 正六边形栅格

假设将机器人分别置于起点栅格S1和S2，令其分别移动到终点栅格D1和D2，2种地图中起点和对应终点之间的直行距离相同。建立路径网络集合N={N1,N2}，其中Ni={Si,Di}，i=1,2。机器人在2种地图中的路径长度代价见表1。

表1 机器人路径长度代价Table 1 Path length cost of robot

由表1可知，就单个机器人来说，正六边形栅格地图下的路径长度代价小于正方形栅格地图的路径长度代价，从单个机器人的路径规划来看，正六边形栅格地图更有利于获得最短路径。

通过3个性能方面的分析比较，得出正六边形栅格比传统正方形栅格更适合于机器人工作环境的建模。

2 多个协同操作的机器人启发式路径搜索算法

本文主要研究多个协同操作的机器人并行移动的路径规划问题，在正六边形栅格地图建模的基础上，采用改进的启发式路径搜索算法对多个机器人的路径进行优化。

多个协同操作的机器人路径规划目标是在避免机器人之间碰撞及机器人与障碍物碰撞的前提条件下，最小化每个机器人的路径长度(即路径上的栅格数量)和消耗时间。假设有m个机器人，建立路径网络集合N={N1,N2,…,Ni}，i=1,2,…,m，路径长度由该路径上所用栅格总数乘以w来表示，则有

(1)

式中：(xit,yit),(xjt,yjt)分别为第i个和第j个机器人在t时刻的栅格位置，j=1,2,…,m；(xit+1,yit+1),(xjt+1,yjt+1)分别为第i个和第j个机器人在t+1时刻的栅格位置；g(Ni)为第i个机器人路径上的栅格数量。

采用改进的启发式估计函数来规划多个协同操作的机器人路径，该函数决定了当前机器人所在位置所有相邻栅格中哪一个即将被机器人遍历。依据机器人已经遍历的栅格数Ztn和候选栅格与该机器人目标栅格之间的变形曼哈顿距离L，该启发式估计函数可评估出相邻栅格的适应度值Gf，函数表达式为

Gf=Ztn+L

(2)

多个协同操作的机器人启发式路径搜索算法流程如图4所示。

图4 多个协同操作的机器人启发式路径搜索算法流程Fig.4 Flow of heuristic path search algorithm of multiple collaborative robots

(1) 设置参数，建立正六边形栅格化的二维环境地图，m个机器人的路径网络集合N={N1,N2,…,Ni}，各个机器人起点、终点及所有障碍物坐标，并初始化路径上遍历的栅格数Ztn=0和机器人路径上遍历的栅格集合为Ø。

(2) 为当前机器人Bi随机生成2条路径R1,R2。

(3) 比较2条路径上的障碍物总数，选择障碍物总数少的路径。

(4) 将起点栅格初始化为当前栅格。

(5) 判断是否遇到障碍物。若没有遇到，则按先前随机生成的路径R1和R2继续移动；若遇到，则判断是静态障碍物还是动态障碍物。

如果障碍物是静态障碍物，则在当前机器人Bi所处栅格创建节点，并计算当前节点栅格所有相邻栅格(障碍物除外)与当前机器人Bi的终点栅格Di之间的变形曼哈顿距离L及对应路径上的转向次数，由此选择Gf最小且转向次数最少的相邻栅格作为下一步移动的位置。如果障碍物是动态障碍物，即其他机器人Bj，分别在Bi和Bj所在栅格创建1个节点，并计算节点栅格所有相邻栅格(Bj占据的栅格除外)与各自的终点栅格Di或Dj之间的变形曼哈顿距离Li和Lj及对应路径上的转向次数。如果Li

(6) 移动到下一个栅格，并判断是否到达终点，如果是则停止寻址；否则返回步骤(5)，直至到达终点为止。

(7) 停止寻址，输出最优路径。

3 仿真实验及结果分析

为了验证基于正六边形栅格地图的多机器人启发式路径搜索算法的可行性和有效性，采用Matlab对不同数量机器人的路径规划进行仿真。为了使机器人在2种环境地图中的路径具有可比性，将地图中所有静态障碍物看作圆形，在2种地图中，每个障碍物的位置和半径都相同，任意机器人的起点和终点位置对应相同。

机器人在2种地图中移动1个栅格的距离相同，同一工作空间分别被分割成30×30个正方形栅格和30×35个正六边形栅格。3个机器人并行移动时的路径如图5所示。仿真收敛曲线如图6所示。不同数量机器人并行移动的路径规划仿真结果见表2。

由图5与图6可知，正六边形栅格地图在路径总长及算法的运行时间上均比正方形栅格地图减少了10%以上，且有效避免了机器人与静态障碍物之间及机器人之间发生碰撞，提高了机器人的安全性。另外，在算法中引入了转向次数，明显提高了机器人运动的平稳性。

由表2可知，随着机器人数量增多，改进的启发式路径搜索算法对正六边形栅格地图下的机器人路径和算法运行时间的优化作用更加明显。因此，正六边形栅格地图与改进的启发式路径搜索算法的结合，可实现对多个并行移动机器人路径的优化，且效果显著。

(a) 正方形栅格地图下的路径

(b) 正六边形栅格地图下的路径

图6 机器人路径仿真收敛曲线Fig.6 Convergence curves of robot path simulation

表2 不同数量机器人并行移动的路径规划仿真结果Table 2 Simulation results of path planning for parallel mobile of different number of robots

4 结论

(1) 从绕障转角、绕障能力及最优路径3个方面，对单个机器人在正方形和正六边形栅格地图中进行比较分析。在正六边形栅格地图中，遇到静态障碍物转弯时，转角和绕行时间都减小，提高了运动的安全性、平稳性及绕障能力，且最优路径长度有所减小。

(2) 正六边形栅格地图与改进的启发式路径搜索算法的结合，实现了对多个并行移动的矿井机器人路径的优化，达到了各机器人路径最短的优化目标，同时避免了机器人之间及机器人与静态障碍物之间发生碰撞。

(3) 仿真结果表明，正六边形栅格地图在路径总长及算法运行时间上均比正方形栅格地图减少了10%以上，且有效避免了机器人与静态障碍物之间及机器人之间发生碰撞，提高了机器人的安全性；随着机器人数量增多，改进的启发式路径搜索算法对正六边形栅格地图下的机器人路径和算法运行时间的优化作用更加明显。