电主轴热特性研究

朱振学，杨 林

(沈阳工业大学 机械工程学院，辽宁 沈阳 110870)

0 引言

电主轴是机床的最核心部件，同时也是机床中最大的热源[1]。由于机床在结构上采用高刚度设计，所以外载荷导致的弹性变形较小。然而电主轴在运行中的发热却是不可避免的，机床热误差约占加工总误差的40%～70%[2]，因此对于电主轴单元来说，需要具备良好的热-结构性能。

本文以某企业的大型螺旋锥齿轮加工中心GTMC-2500的铣削电主轴为研究对象，着重利用有限元分析方法对电主轴的热-结构特性进行分析和研究。

1 电主轴热载荷计算

在电主轴工作过程中，热源主要为电机定转子和轴承。电主轴结构如图1所示。

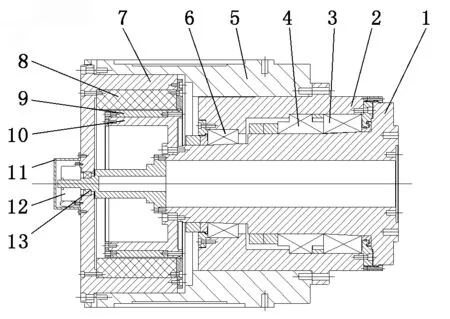
1-主轴；2-外壳；3-前轴承；4-中轴承；5-摆动体；6-后轴承；7-定子连接套；8-定子；9-转子；10-转子连接套；11-编码器保护罩；12-角度编码器；13-尾轴承

1.1 电机生热

电机损耗主要包括机械损耗、电损耗、磁损耗和附加损耗[3]。其中附加损耗约占额定功率的1%～5%[4]。主轴电机损耗功率均转化为热量，由于定、转子消耗功率比例约为2∶1，所以生热率q即单位体积的生热功率的计算公式为：

(1)

其中：q为体生热率，W/m3；I为工作电流，A；R为电阻，Ω；V为热源体积，m3。

1.2 主轴轴承生热

轴承生热主要是滚动体与内圈、外圈、保持架及润滑剂摩擦造成的[5]。根据经验公式，轴承摩擦发热计算公式为：

(2)

其中：Qf为轴承摩擦生热，W；M1为轴承摩擦力矩，N·mm；n为轴承转速，r/min。轴承摩擦力矩可由载荷力矩与黏性摩擦力矩之和表示：

M=M0+M1.

(3)

其中:M0为黏性摩擦力矩，N·mm；M1为载荷力矩，N·mm。黏性摩擦力矩计算公式为：

(4)

其中:ν为润滑剂的运动黏度，mm2/s；Dm为轴承的平均直径，mm；f0为与轴承类型和润滑方式有关的系数。轴承载荷力矩M1计算公式为：

M1=f1P1Dm.

(5)

其中：f1为与轴承类型、额定载荷及当量静载荷有关的系数；P1为轴承所受载荷，N。

2 电主轴有限元分析

2.1 瞬态热分析

使用SolidWorks软件对电主轴进行三维建模并化简，使用Workbench软件对其进行有限元分析。设定初始温度31 ℃，经计算电主轴在24 000 s时的温度场云图如图2所示。

由图2可以看出，电主轴温度最高区分布在电机定转子处，温度约为45 ℃。分析其主要原因是电机定转子生热较多，且散热条件不好，无法排出热量，导致电机定转子温升较高。图3为电主轴最高温度变化曲线。从图3中可知，电主轴前几分钟升温较快，之后逐渐减缓，400 min后温度增长较慢。

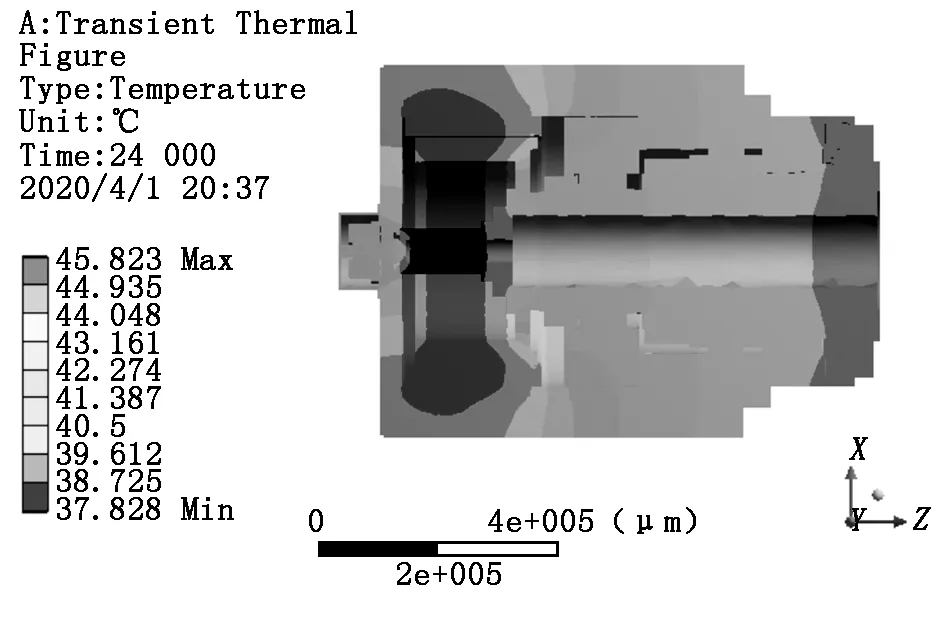
图2 电主轴温度场云图

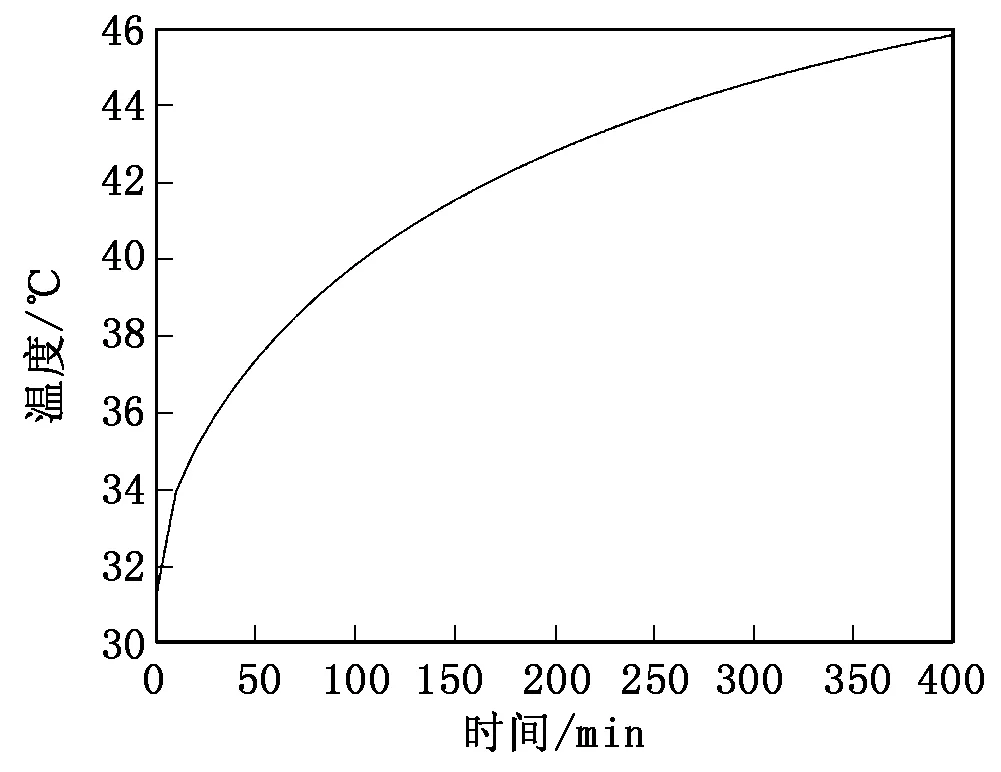
图3 电主轴最高温度变化曲线

2.2 热-结构耦合分析

经计算得到未加冷却的电主轴在24 000 s时的热变形云图，如图4所示。使用探针功能提取主轴端部外圆x、y方向和端面处z方向热变形值，读取24 000 s变形值及初始温度变形值，通过相减可知：x方向热变形为13.9 μm，y方向热变形为16.1 μm，z方向热变形为75.7 μm。x、y方向变形云图围绕主轴轴线呈对称分布，可见x、y方向变形主要由端部零件受热膨胀引起，对加工精度影响较小；z方向的变形沿主轴轴线，对加工精度的影响较大。

3 电主轴升温实验

为了验证前面仿真模型的正确性，对电主轴进行

升温实验，实验仪器使用红外测温仪，设定主轴转速为165 r/min，测温点选择前轴承及外壳倒角处，测试时间为24 000 s，温度曲线如图5所示。实验曲线与仿真曲线基本一致，说明了仿真模型的正确性，可以使用该模型对电主轴的运行状况进行研究。

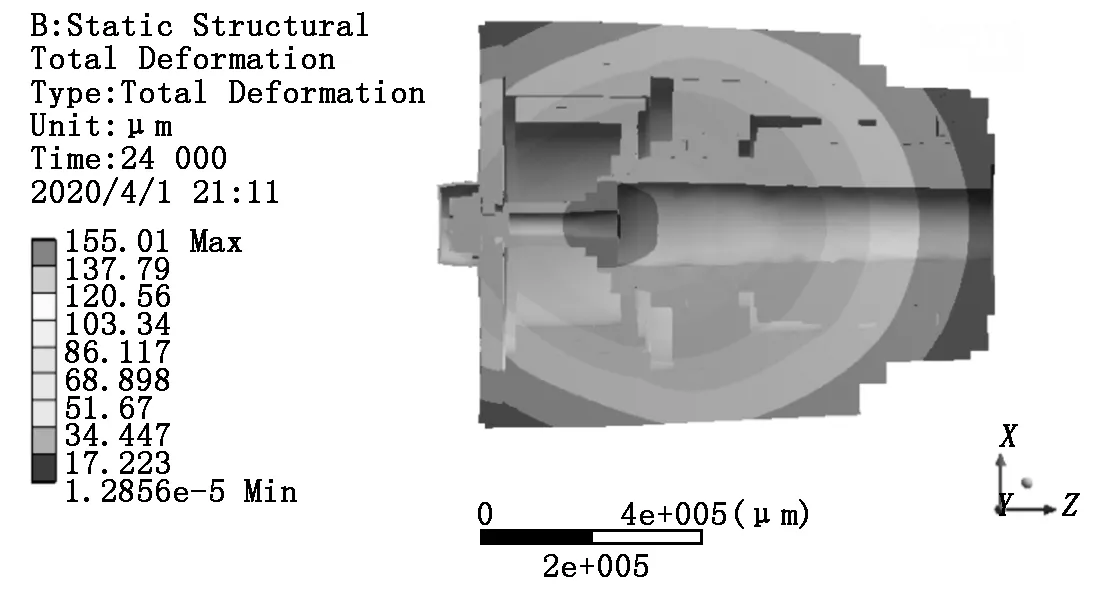
图4 主轴变形云图

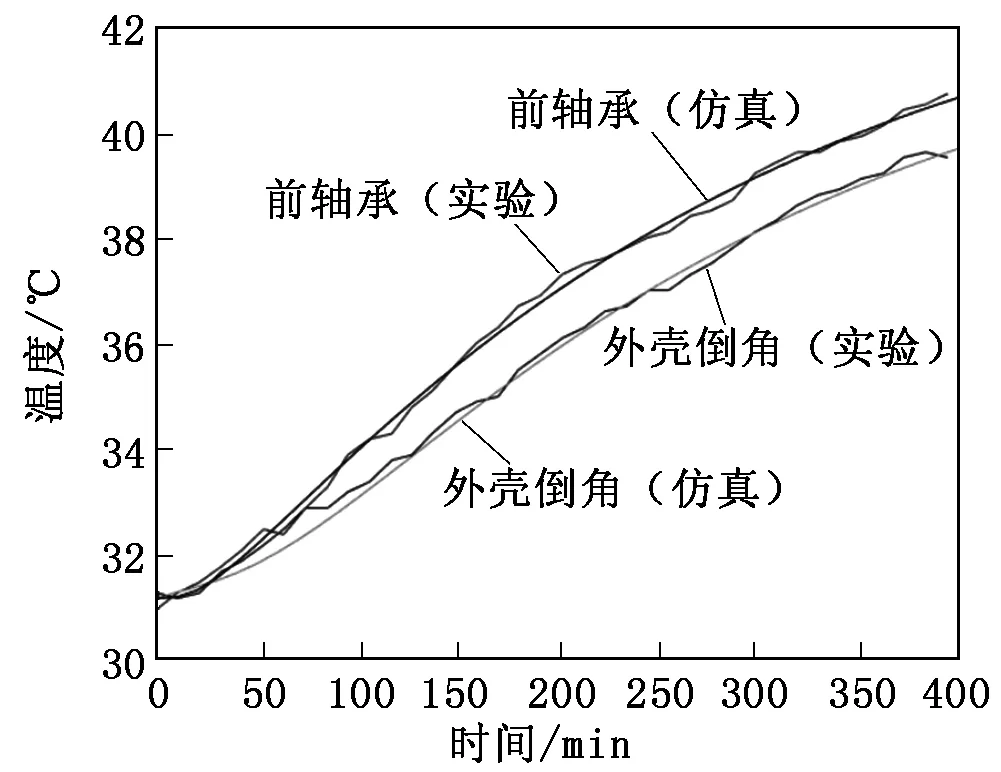
图5 外壳倒角及前轴承升温曲线

4 结论

(1) 通过实验可知，该电主轴的仿真模型具备有效性，且该型号的电主轴热源主要为主轴电机的损耗发热。

(2) 热-结构耦合分析表明，电主轴主要误差来源为z方向，最大误差为75.7 μm。