基于手眼关系与基坐标关系的协作焊接机器人标定

燕 浩，程小虎，杨正蒙，张 聪

(1.合肥工业大学 机械工程学院，安徽 合肥 230000；2.武汉工程大学 机电工程学院，湖北 武汉 430200)

0 引言

焊接机器人技术在工业生产中具有十分重要的地位[1]，而多机协作进一步弥补了焊接工况中出现的横焊、平焊等焊接位置无法达到满意焊接要求的不足，能够有效地提高焊接效率与焊缝质量。

对于复杂的焊接轨迹和焊枪等部件经高温产生的变形，通过传统的再示教方法很难实现误差补偿，为了解决此类问题，基于视觉的相机标定技术应运而生，有效地提高了焊接效率和焊接质量[2]。

基于视觉的双机器人协作系统最常用的手眼标定方法是Tsai提出的转站法[3]，使机器人运动形成三种不同的姿态，并利用摄像机拍摄参数已知的参照物，然而该方法仅针对单个机器人标定，未对双或多机器人系统整体标定给出具体方法。文献[4]提出一种利用机器人末端法兰为特征解算出相机外参的手眼标定方法，另外采用激光跟踪仪测量基坐标关系，该方法的优点是不需要外设标靶即可进行手眼标定，但较为复杂，很难应用到实际生产中。

对于双机器人基坐标的标定方法常用的有三点法和六点法，其中三点标定方法的典型代表任永杰等[5]利用激光仪和线性方程对机器人进行误差估计，可使标定精度提高一倍以上，但在实际使用中成本较高。除此之外，机器人标定还有一些其他的方法，如视觉自动标定方法和神经网络法等[6]。

目前，针对双机器人协作运动系统的标定没有较为可行的方法，均是对多机器人基坐标系和相机与工具坐标系进行分别标定后构建系统模型，此类方法由于二次标定带来了双重误差。为此，本文以两台FANUC 200iD/4S工业机器人组成的双机器人协作系统为例，提出了一种基于视觉的机器人协作系统联合标定方法。该方法同时采用三点共圆的基坐标标定法与成像对称的张正友手眼标定法，通过相机对标定参照物进行标定作业，同时完成基坐标标定，从而快速得到手眼标定参数，形成完整协作机器人系统的标定参数，其具有操作简单、标定精度高、适用范围广等优点。

1 焊接机器人建模与运动学分析

FANUC 200iD/4S工业机器人是典型的6轴旋转关节式机器人，末端具有6个自由度，依据D-H参数法[7]建立的单个机器人初始状态坐标系如图1所示，各连杆D-H参数如表1所示。

图1 FANUC 200iD/4S机器人初始状态坐标系

(1)

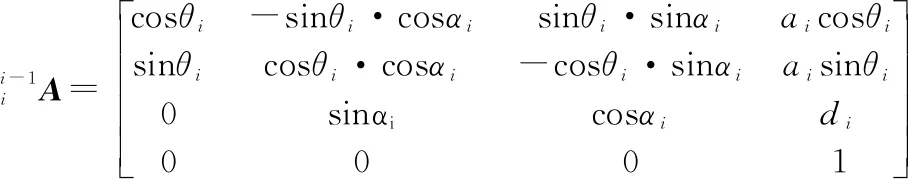
表1 FANUC 200iD/4S机器人D-H参数

2 协作焊接机器人标定方法

2.1 构建协作机器人系统模型

图2为建立的双机器人系统模型。其中，{R1}为左侧抓取机器人基坐标系，也是协作机器人系统的冠以坐标系，{R2}为焊接机器人基坐标系，{Tc}为相机坐标系，{T1}为标定板坐标系，{T2}为机器人工具坐标系，H1为{T1}到{R1}的坐标转换关系，H2为{R1}到{R2}的坐标转换关系，H3为{R2}到{T2}的坐标转换关系，H4为{Tc}到{T1}的坐标转换关系，HTcT2为{Tc}与{T2}之间的坐标转换关系。一台机器人负责抓取焊接工件，另一台机器人负责焊接任务，摄像机和顶针分别固定在右侧焊接机器人手臂和末端执行器上，标定板位于左侧机器人的末端执行器上。因此其手眼关系通过双机器人系统闭环运动关系表达为：

(2)

其中：R、T分别为相机坐标系到工件坐标系的旋转矩阵和平移矩阵。

H1和H3可由式(1)和示教器得到，若要形成系统完整的运动关系，还需要在得知两机器人基坐标之间的位姿关系即H2的同时通过机器视觉对棋盘靶的特征角点求出H4。

图2 建立的双机器人系统模型

2.2 基于三点标定法的机器人基坐标标定

图3为双机器人系统的三点标定法原理。其标定原理如下：设定标定板的中心与搬运机器人末端坐标系重合，即T1的中心为标定板中心点，操作机器人R2的示教器使其末端移动到一个合适的位置，并保持关节1角度为0，即θ1=0°，确保共圆面，且圆心为O3；然后控制机器人R1运动，使其标定板的中心与机器人R2顶针接触，记为点M1(xM1,yM1,zM1)，同时通过示教器读取两个机器人θ1～θ6的关节数据，即完成一次数据读取；随后仅调整机器人R2的关节1转动θ角度，控制机器人R1运动使标定板的中心与顶针接触，记为点M2(xM2,yM2,zM2)，并记录关节角度；最后调整机器人R2的关节1转动角度，重复控制机器人R1运动使标定板的中心与顶针接触，记为点M3(xM3,yM3,zM3)，并记录数据。

图3 双机器人系统“三点法”标定原理

M1、M2和M3三点共圆，可根据坐标关系求出其圆心坐标O3(xO3,yO3,zO3)，因为O3点是仅在焊接机器人基坐标系竖直方向上进行平移的一个点，所以：

(3)

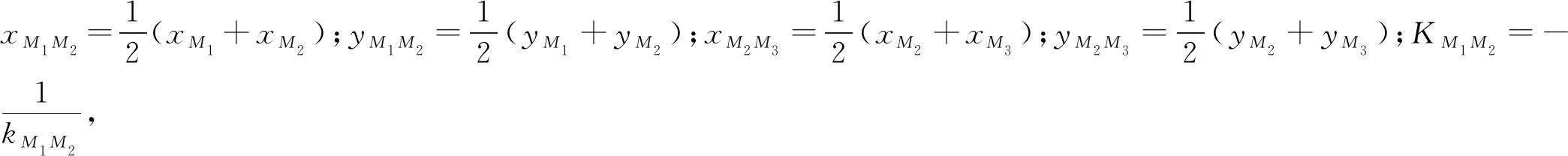
取任意一个接触点求得共圆半径为：

(4)

进一步设O3所在坐标系的x、y、z方向单位矢量分别为e=[ex,ey,ez]T，q=[qx,qy,qz]T，n=[nx,ny,nz]T则：

(5)

(6)

q=n×e.

(7)

因此可求得坐标系{R2}圆心坐标为：

(8)

其中：Δz为O2与O3竖直方向上的距离，可由焊接机器人示教器和运动学关系得到。因此，求得{R2}相对于{R1}的变换关系H2：

(9)

2.3 基于张正友法机器人手眼标定

机器人的手眼标定是求出机器人相机坐标系{Tc}与机器人工具坐标系{T2}之间的坐标转换关系HTcT2。在式(2)与式(9)基础上需进一步求出相机坐标系与搬运机器人末端坐标系的关系H4，即相机的外参矩阵，这里采用张正友[8]棋盘标定法。设点P在世界坐标系下的齐次变换矩阵为wP[wx,wy,wz,1]T，由于CR200型相机的模型为线性模型，假设图像未发生畸变，P′=[u,v,1]T为像素的投影点，可将世界坐标系与投影坐标系进行简化，即：

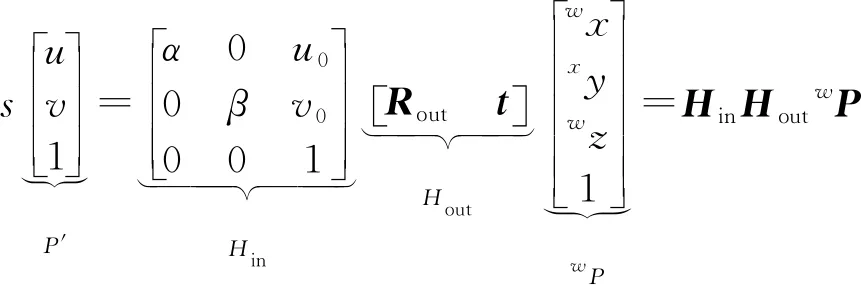
(10)

其中：s为非零比例系数；Hin∈R3×3,为相机内参矩阵；α、β、u0、v0为内参矩阵参数；Hout∈R3×4，为相机外参矩阵；Rout=[r1,r2,r3]∈R3×3，为旋转矩阵，r1、r2、r3分别为相机坐标系绕世界坐标系3个轴的旋转矢量；t=[tx,ty,tz]T∈R3×1，为空间中平移矩阵。由于所有标定点位于同一平面，假设wP的wz=0，式(10)改写为：

(11)

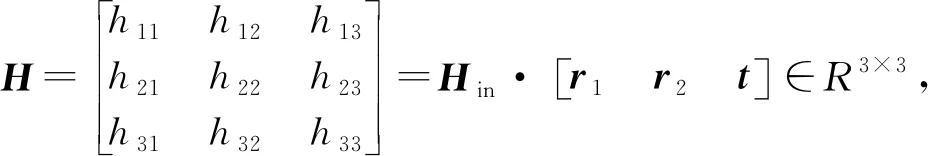
(12)

由于Rout为单位正交矩阵，则r1与r2有如下关系：

(13)

(14)

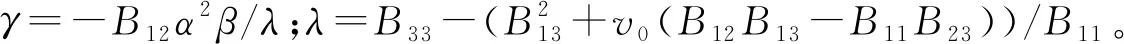
外参矩阵相关参数为：

(15)

3 实验及分析

为了验证上述标定方法的可行性，搭建了如图4所示的双机器人系统标定平台，由两台FANUC 200iD/4S工业机器人、径长95 mm顶针、氧化铝刻蚀标定板、CR200型工业相机及操作平台组成。

图4 搭建的双机器人系统标定平台

本实验主要需要采集两方面的数据：①三次标定过程中每个接触点的机器人6个关节角数据；②机器人在调节过程中相机对搬运机器人所持的标定板进行识别的结果。

标定操作过程如2.2小节所述。为了减少实验中人为因素产生的误差，本实验重复5次，并记录数据，如表2所示。

表2 FANUC 200iD/4S双机器人基坐标标定时各关节角度

值得注意的是，在进行靶点识别实验时需要在合适的光照前提下。本实验利用Ubuntu 16.04进行环境搭建，调用findChessboardCorners对采集的多幅图像进行靶点的自动识别、提取处理，每幅图42个角点，若单幅图没有42个角点，该幅图即会被剔除。其中的两组靶点识别如图5所示。

标定板采用边长为10 mm的正方形格子高精度标定板，对提取的42个靶点进行标定计算，根据式(14)、式(15)得到CR200型工业相机内参矩阵为：

(16)

由于在相机自动识别标定板靶点的过程中，相机与标定板之间的位置关系是不断变化的，因此每一幅图像对应的外参都不一样，图5(b)和图5(c)两组靶点相机的外参矩阵分别为：

(17)

(18)

进一步采用MATLAB对表2中数据进行计算，得到搬运机器人与焊接机器人之间的基坐标系转换关系：

(19)

将式(16)、式(17)、式(19)计算结果代入运动学闭环链式(2)中进行计算，得到焊接机器人手眼关系为：

HTcT2=H4·H1·H2·H3=

(20)

图5 手眼标定时靶点自动识别

将式(20)结果重新导入机器人示教器中，并将计算关节数据导入至示教器进行重复定位验证，所测顶针的顶尖与标定板靶点的距离误差小于0.15 mm，如图6所示。该实验结果满足焊接工况要求。

图6 顶针碰撞精度验证

4 结论

本文提出了基于手眼关系与基坐标关系的协作机器人快速标定方法。该方法采用三点法与张正友标定法可以同时完成对手眼关系及基坐标关系的数据采集，以此完成标定任务。实验结果通过再示教表明其标定误差在0.15 mm之内，满足较高精度要求和工作环境要求，有较强的实用价值。