三容对象临界比例度法的参数计算与仿真实验
2020-08-25谢迎新
彭 程, 谢迎新
(华北科技学院电子信息工程学院,河北三河065201)
0 引 言
临界比例度法,又称稳定边界法[1]、连续循环法[2],是一种重要的PID参数整定方法,在四旋翼飞行器稳定控制[3]、罗茨风机风量调节[4]、温度控制[5-7]、直流电机调速[8]、船用升降设备位置控制[9]、反应堆功率控制[10]以及变量施肥控制[11]等不同控制问题中均有成功应用。
自动化专业本科“过程控制系统”课程中会讲授临界比例度法,实验课也经常会针对该方法开展训练[12-15]。在以往的教学实践中,通常只是将临界比例度法作为一种PID参数整定方法加以介绍,一般不会将该方法与“自动控制原理”课程中讲授过的系统稳定性判据联系起来,学生也只是将临界比例度法理解为一个独立的知识点。使用临界比例度法的关键是通过实验得到临界比例系数和等幅振荡周期。对于一些特定形式的被控过程,如果已知被控对象、执行器和测量变送器的数学模型,上述两个参数是可以计算出来的。文献[1,10]中均提出过这一观点,并分别采用奈奎斯特稳定判据和根轨迹法进行了计算,但是没有进行详细的理论分析。本文以有自衡特性和无自衡特性3容对象为例,给出了临界比例度法参数的计算公式,并设计了Matlab/Simulink仿真实验,以便于学生更好地理解和掌握该方法。
1 临界比例度法
考虑图1所示的单回路控制系统,图中R(s)、E(s)、U(s)、Y(s)和B(s)分别为系统的参考输入、偏差、控制量、被控量和反馈量,C(s)、Gv(s)、Gp(s)和Gm(s)分别为控制器、执行器、被控对象和测量变送器的传递函数。
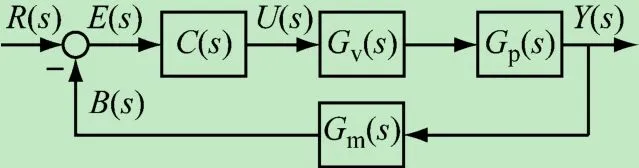
图1 单回路控制系统结构图
若Y(s)和B(s)在阶跃型参考输入R(s)和增益为临界比例系数Kc的比例控制器C(s)作用下产生周期为Tc的等幅振荡,则PID控制器

的3个参数:比例系数KP、积分时间常数TI和微分时间常数TD,可以由表1 确定[1]。

表1 临界比例度法PID控制器参数计算
临界比例度法不需要已知被控对象、执行器和测量变送器的数学模型,只需在实验过程中逐步增大比例控制器的比例系数,直到Y(s)和B(s)产生等幅振荡,记录临界比例系数Kc和等幅振荡的周期Tc的值,就可以确定PID控制器的参数。
2 临界比例度法参数的解析计算
2.1 有自衡特性3容对象
如前所述,临界比例度法的关键问题是确定参数Kc和Tc的值。本节针对有自衡特性3容对象
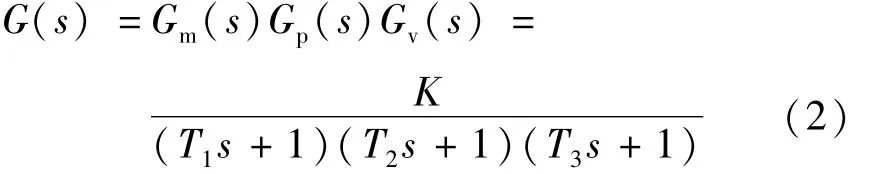
式中:K >0为对象增益;T1>0、T2>0、T3>0为时间常数。为研究参数Kc、Tc与模型参数T1、T2、T3以及K之间的关系,给出下面的引理。
引理1 对于正常数T1、T2和T3,有
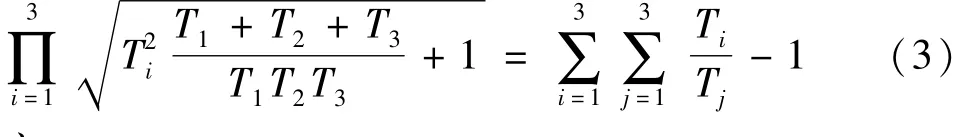
成立。
证明:令

则
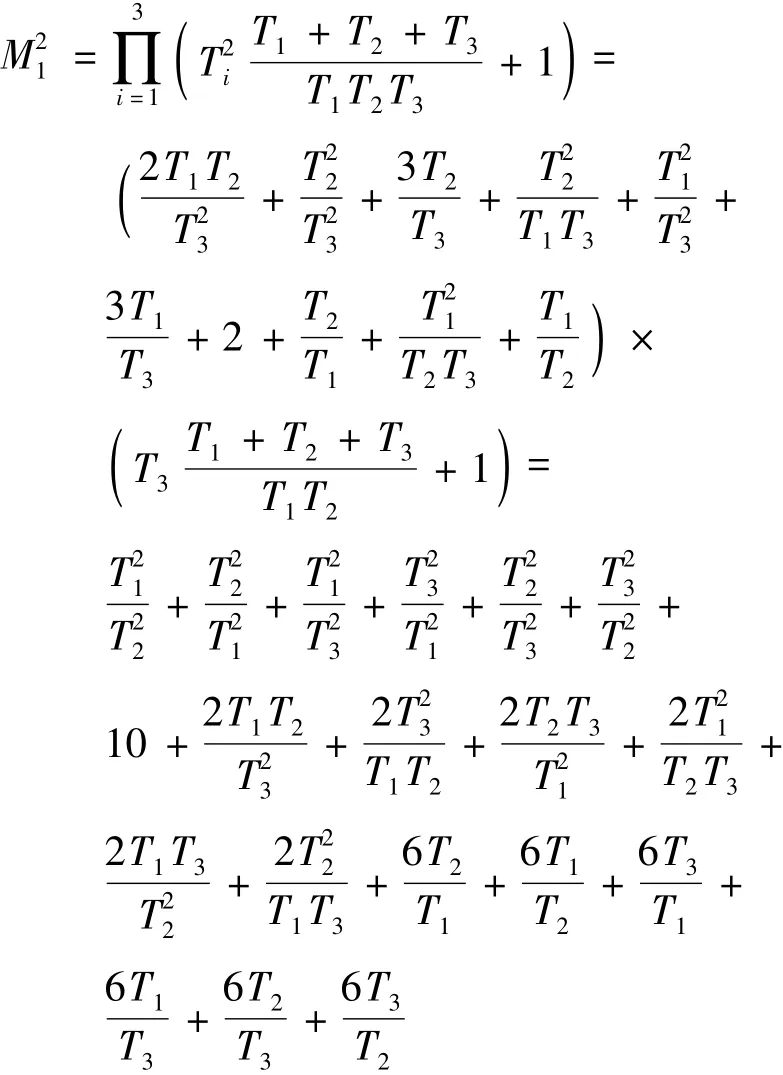
由多项和平方展开公式计算可得:

易知M1>0,M2>0,故M1=M2成立。证毕。
引理2 对于正常数T1、T2和T3,有成立。
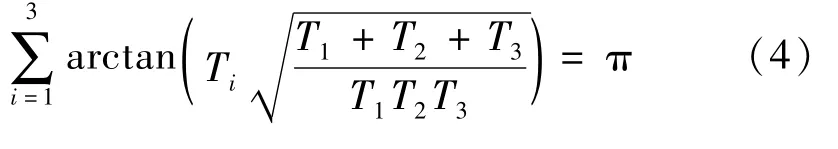
证明 因为

同时考虑到
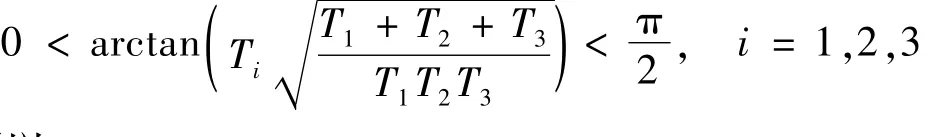
所以

成立。证毕。
在引理1和引理2的基础上,可以给出如下的定理。
定理1 对于式(2)给出的有自衡特性3容对象,若已知模型参数T1、T2、T3和K,令比例控制器
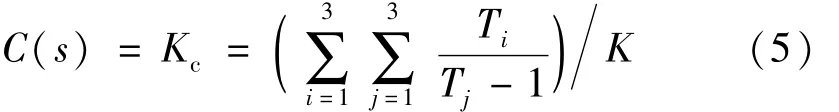
则Y(s)和B(s)在单位阶跃参考输入R(s)=1/s作用下将产生等幅振荡,且等幅振荡的周期

证明 (1)证法1。
由引理1可知,


由上述计算结果可知,以C(s)=αKc为比例控制器的开环系统的幅相特性曲线经过复平面上的(-α,j0)点,对应的频率为ωc。
根据奈奎斯特稳定判据容易知道,当α>1时,开环幅相特性曲线顺时针包围(-1,j0)点两次,闭环系统不稳定,并且有两个不稳定闭环极点;当α<1时,开环幅相特性曲线不包围(-1,j0)点,闭环系统稳定;而α=1,即比例控制器C(s)=Kc时,闭环系统临界稳定,阶跃输入下闭环系统响应会出现等幅振荡,且振荡周期
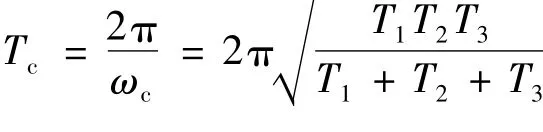
证毕。
(2)证法2。
比例控制器C(s)=Kc作用下闭环特征多项式

对闭环特征多项式列劳斯表,有

劳斯表s1行中

即劳斯表出现了全0行,闭环系统必然存在位于实轴或者虚轴上的、关于原点对称的极点。由劳斯表s2行构造辅助方程
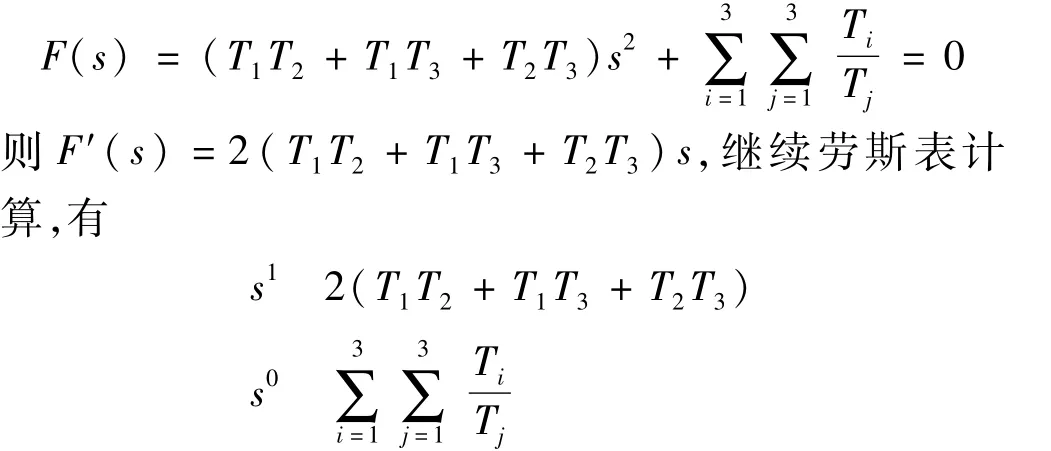
容易知道构造辅助方程之后劳斯表第一列元素均为正,故闭环系统没有实部大于零的极点,即关于原点对称的闭环极点是位于虚轴上的,而第3个闭环极点位于负实轴上。解辅助方程可得虚轴上的共轭虚数极点
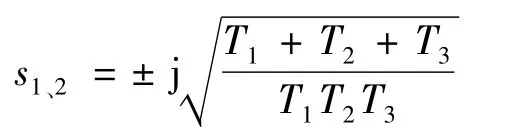
故在比例控制器C(s)=Kc作用下闭环系统临界稳定,阶跃响应会出现等幅振荡,且振荡周期

证毕。
(3)证法3。
由根轨迹分析可知,不管比例控制器的比例系数KP如何变化,根轨迹3个分支之中有1个分支始终位于负实轴上,即闭环系统总有1个稳定的闭环实极点;而另外2个分支在离开负实轴之后会随着比例系数KP的增大,逐渐靠近并穿越虚轴。即随着比例系数KP的增大,闭环系统会呈现出稳定、临界稳定到不稳定的变化规律。
比例控制器C(s)=Kc时,闭环特征多项式

令D(s)=0,可得闭环极点为

和
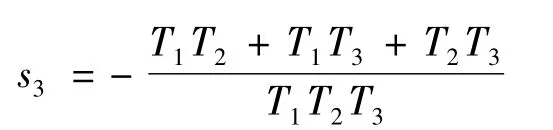
闭环系统的3个极点分别位于虚轴和负实轴上,故比例控制器C(s)=Kc作用下闭环系统临界稳定,闭环系统阶跃响应会出现等幅振荡,且振荡周期
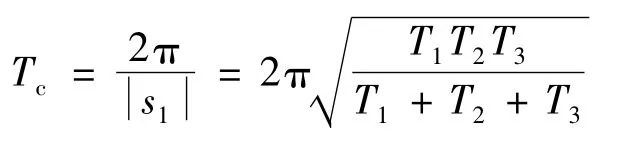
证毕。
定理1的3种证明方法将“自动控制原理”和“过程控制系统”两门课的知识点联系起来,分别从奈奎斯特稳定判据、劳斯稳定判据和根轨迹法的角度揭示了有自衡特性3容对象临界比例度法参数Kc、Tc的取值规律。
2.2 无自衡特性3容对象
对于无自衡特性3容对象

式中:T1>0、T2>0、T3>0为时间常数。其临界比例度法参数Kc和Tc的计算原理可以由下面的定理2给出。与定理1的证明过程类似,可以从奈奎斯特稳定判据、劳斯稳定判据和根轨迹法3种角度出发进行证明。这里仅给出使用奈奎斯特稳定判据的证明方法。
定理2 对于式(7)给出的无自衡特性3容对象,若已知模型参数T1、T2和T3,令比例控制器
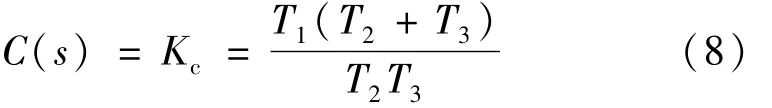
则Y(s)和B(s)在单位阶跃参考输入R(s)=1/s作用下将产生等幅振荡,且等幅振荡的周期

证明 设比例控制器

式中:β>0为正常数,则系统开环传递函数

令s=jω,可得开环系统频率特性
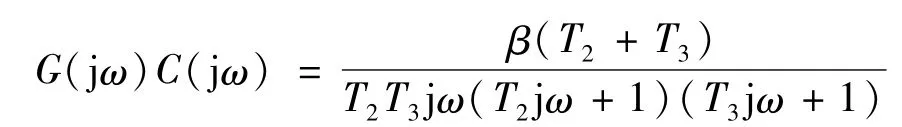
令

将ωc代入开环幅频特性和相频特性的表达式,可得
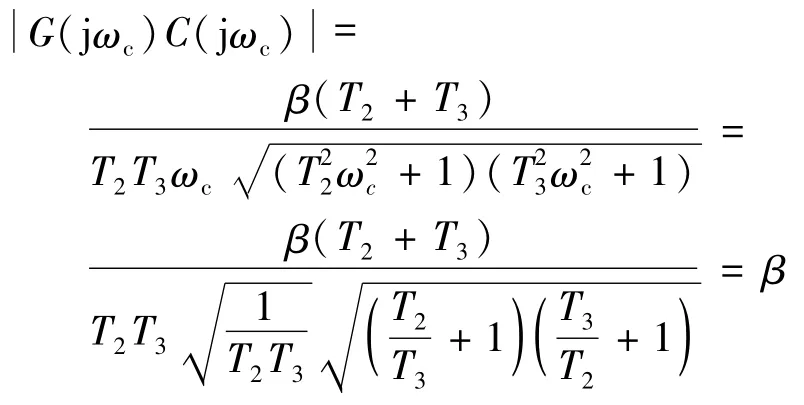
以及

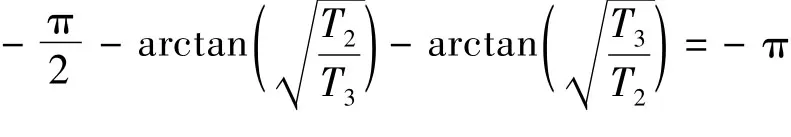
由上述计算结果可知,以C(s)=βKc为比例控制器的开环系统的幅相特性曲线经过复平面上的(-β,j0)点,对应的频率为ωc。
根据奈奎斯特稳定判据容易知道,当β>1时,闭环系统不稳定;当β<1时,闭环系统稳定;而β=1,即比例控制器C(s)=Kc时,闭环系统临界稳定,阶跃输入下闭环系统响应会出现等幅振荡,且振荡周期
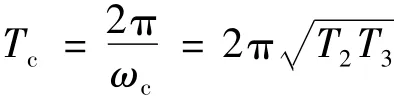
证毕。
3 仿真实验设计
在教学实践中,使用了Matlab/Simulink软件进行临界比例度法仿真实验。在使用Matlab/Simulink软件模拟3容对象的临界比例度法参数调节过程之后,可以使用定理1和定理2计算出参数Kc、Tc的理论值,以检验参数整定过程的正确性。要求学生完成的实验内容包括:
①针对有自衡特性3容对象,根据图1建立Simulink仿真文件。
②取消积分和微分控制作用,逐步增大比例控制器的比例系数,使闭环系统阶跃响应呈现等幅振荡,记录临界比例系数Kc和等幅振荡的周期Tc的值。
③按照表1的规则,编写Matlab程序计算P、PI和PID控制器参数,将参数写入Simulink仿真文件,进行仿真,记录峰值时间、超调量、调节时间和稳态误差,比较不同控制器作用下闭环系统响应的特点。
④编写Matlab程序计算临界比例度法参数的理论值,并与②中的结果进行对比,如果不一致,找出原因。
⑤改变Simulink仿真文件中被控对象的模型参数,使其成为无自衡特性3容对象,重复②~④的仿真内容。
在实验课之前,向学生讲授定理1及其证明方法,要求学生利用课余时间使用奈奎斯特稳定判据、根轨迹法或者劳斯稳定判据之中的一种方法自行分析临界比例度法参数与无自衡特性3容对象模型参数之间的关系,并进行理论证明,以培养学生的理论分析能力。
4 数值算例
限于篇幅,本节使用两个算例进一步验证定理1和定理2的正确性,不展示临界比例度法参数整定过程和控制效果,两例中均假设Gv(s)=1、Gm(s)=1。
例1 有自衡特性3容对象

其模型参数为T1=2 s、T2=10 s、T3=20 s和K =3。
由定理1计算可得Kc=6.600 0,进而可以求出ωc= 0.282 8 rad/s,Tc= 22.214 4 s。比例控制器C(s)=6.600 0作用下闭环系统的单位阶跃响应如图2所示。观察图2可知阶跃响应出现了等幅振荡,并且振荡周期与理论计算结果一致,验证了定理1的正确性。

图2 有自衡特性3容对象的闭环单位阶跃响应
例2 无自衡特性3容对象

其模型参数为T1=0.2 s、T2=2 s和T3=7 s。
由定理2计算可得Kc=0.128 6,进而可以求出ωc= 0.267 3 rad/s,Tc= 23.509 5 s。比例控制器C(s)=0.128 6作用下闭环系统的单位阶跃响应如图3所示。与例1的情况类似,观察图3可以验证定理2正确性。
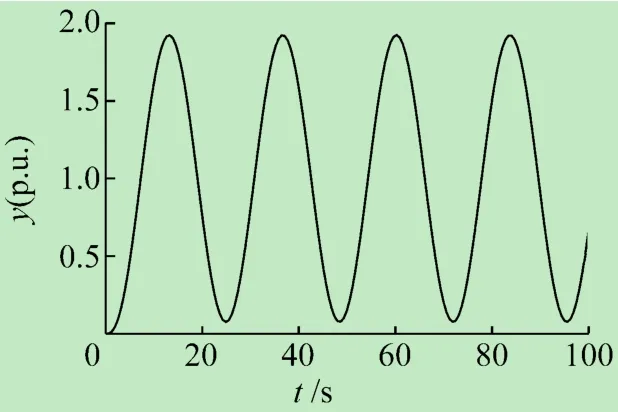
图3 无自衡特性三容对象的闭环单位阶跃响应
5 结 语
针对有自衡特性和无自衡特性3容对象这两类典型的过程控制对象,研究了临界比例度法参数与模型参数之间的关系,以此为基础,设计了临界比例度法Matlab/Simulink仿真实验。具体结论如下:
(1)对于有自衡特性3容对象,临界比例系数Kc是模型参数T1、T2、T3和K的显函数,等幅振荡周期Tc是T1、T2、T3的显函数;对于无自衡特性3容对象,Kc是模型参数T1、T2和T3的显函数,Tc是和T2和T3的显函数。
(2)使用“自动控制原理”课程讲授过的稳定性判别方法证明了3容对象临界比例度法参数与模型参数之间的关系。在理论指导下设计了临界比例度法Matlab/Simulink仿真实验,有利于学生更好地掌握该方法,提升理论分析和实践能力。
